
语言类层次
正则语言
有限状态机(finite state machine,FSM),也称为有限状态自动机(finite state automata,FSA)。有限状态机的一个重要属性是保证对任何有限长度的输入字符串能够停止。把某个FSM能够接收的语言类称为正则(regular)语言类。
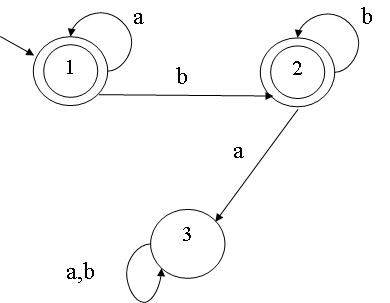
简单FSM
描述万维网对象的统一资源标识符(URI)语言是正则的。
确定性有限状态机(DFSM)
形式上,确定性有限状态机M是个五项式(K,Σ,σ,s,A),其中:
- K是有限状态集。
- Σ是输入字母表。
- s∈K是开始状态。
- A⊆K是一组接受状态。
- σ是转变函数,映射:F(状态)×Σ(输入符号)to K(状态)。
影响M今后的行为:
- 当前状态。
- 待读输入。
定理1 DFSM停止
定理:每个DFSM M,输入为w时,均在|w|步之后停止。
证明:输入为w,M执行计算C0|-MC1|-MC2|-M...|-MCn,其中C0是初始配置,Cn形如(q,ε),其中状态q∈KM。Cn为接受或拒绝配置,因此M到达Cn时停止。计算中每一步消耗w的一个字符,因此n=|w|,故M在|w|步之后停止。
例子:缺字母语言
设∑={a,b,c,d},设LMissing为{w:w中不出现符号ai∈∑}。LMissing是个正则语言,可以写出接受这个语言的DFSM M。需要下列状态:
- 开始状态:所有字母都缺。
读一个字符后,M可能是
- 读取a,因此b,c,d缺。
- 读取b,因此a,c,d缺。
- 读取c,因此b,a,d缺。
- 读取d,因此b,c,a缺。
读第二个字符后,M可能还是上述状态,也可能变成
- 读取a和b,因此c,d缺。
- 读取a和c,因此b,d缺。
- 共六种情形。
读第三个字符后,M可能还是上述状态,也可能变成
- 读取a、b、c,缺d。
- 读取a、b、d,缺c。
- 读取a、c、d,缺b。
- 读取d、b、c,缺a。
读第四个字符后,M可能还是上述状态,也可能变成
- 四个字符都读取,不缺。
除了最后一个状态,每个状态都可接受。M很复杂,但可以写出来。现在假设∑是整个英文字母表,则也可以写出接受LMissing的DFSM,但太复杂了,很容易出错,这时DFSM模型不再适用。
非确定性FSM
为了解决上面的缺字母问题,可以修改FSM定义,允许非确定性。
什么是非确定性FSM
非确定性FSM(或NDFSM)M的五项式为(K、∑、Δ、s、A),其中:
- K为有限字符集。
- ∑为字母表。
- s∈K为开始状态。
- A⊆K为最终状态。
- Δ为转换关系,其为(K×(Σ∪{ε}))×K的有限子集。
换句话说,Δ的每个元素包含一个(状态,输入符号或ε)对和一个新状态。
配置、初始配置、接受配置、yield-in-one-step、yields和计算的定义和DFSM相似。设w为Σ*的元素,则
- M接受w的充要条件为至少其中一个计算接受。
- M拒绝w的充要条件为所有计算都不接受。
例子:缺字母语言
设∑={a,b,c,d},设LMissing为{w:w中不出现符号ai∈∑}。下列简单NDFSM M可以接受LMissing:
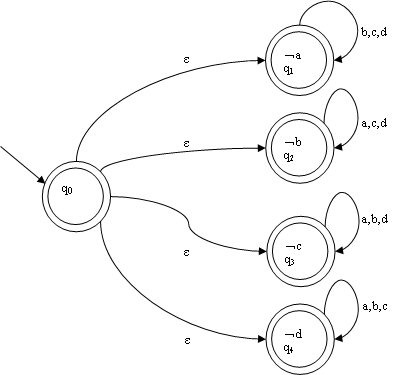
M猜测哪个字母缺,猜对时接受,如果全错,则所有路径失败,M拒绝。
当然,实用字符串搜索引擎是更小和确定的。这样的NDFSM可以作为构造高效搜索引擎的基础。字符串搜索是每个字处理和文本编辑系统的基本操作。
正则语言的规范形式
顺序决策图(OBDD)是布尔表达式的规范形式,是模型检查器可以验证大型并发系统和硬件路线的正确性。
假设FSM具有规范形式,两个FSM具有相同的规范形式的充要条件是接受相同的语言。对象C的规范形式(canonical form)对C的每类等价对象指定唯一表示方法。此外,每种表示方法是独特的,C中两个对象具有相同表示方法的充要条件是其在形式定义上等价。
上下文无关语言
压栈自动机(pushdown automaton,PDA)。把某个PDA能够接收的语言类称为上下文无关(context-free)语言类。
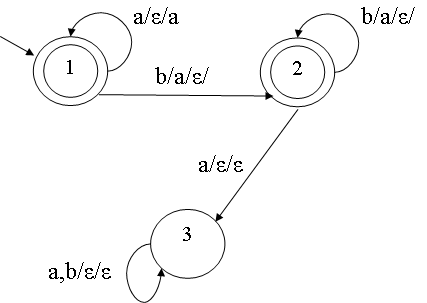
可以接受AnBn的压栈自动机
可确定和半确定语言
图灵机(Turing machine)。
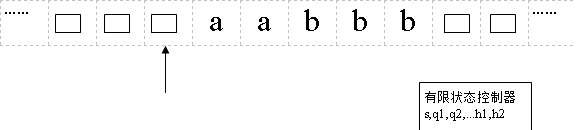
图灵机的结构
我们使用图灵机定义两类语言:
- 可确定(decidable)语言L的充要条件是存在一个图灵机M,对所有输入停机,接受属于L的任何字符串,拒绝不属于L的任何字符串。即M可以判断是否。
- 半确定(semidecidable)语言L的充要条件是存在一个图灵机M,接受属于L的所有字符串,不接受不属于L的所有字符串。对不属于L的字符串,M可能拒绝,也可能永久循环。即M能识别一个解并给予肯定,但可能不知道何时要放弃求解和给予否定。