关于矩阵和向量的相关知识,可能学过后几乎遗忘了干净,或是没有学过,但并不影响我们对相关API的使用。当然基础知识的理解会帮助我们弄明白和更好的进行OpenGL的开发工作。
GLTools库中的Math3d,其中包含了大量的OpenGL 3D数学的数据类型,矩阵、向量的计算等等 API。
一、向量
1、何为向量
3D笛卡尔坐标系中,一个顶点就是 XYZ 坐标空间上的一个点的位置。XYZ 就是一个向量,数学思维中一个顶点就是一个向量。

向量长度为1 的称为单位向量。向量长度 = 2√(x2 + y2 + z2) 即:向量的模。
把一个非单位向量缩放到 1 的过程,称为标准化。也叫做单位化向量。 -- 保留向量的方向
1.1、声明向量
M3DVector3f() -- 3维向量 (x,y,z)
M3DVector4f() -- 4维向量 (x,y,z,w) -- w: 缩放值,不缩放为:1
// 三维向量/四维向量的声明
typedef float M3DVector3f[3];
typedef float M3DVector4f[4];
// 声明一个三维向量
M3DVector3f vVector;
// 声明一个四维向量并初始化一个四维向量
M3DVector4f vVertex = {0,0,1,1};
// 声明一个三分量顶点数组,例如生成一个三角形
M3DVector3f vVerts[] = {
-0.5f,0.0f,0.0f,
0.5f,0.0f,0.0f,
0.0f,0.5f,0.0f
}
2、向量的点乘(dot product)
两个向量之间可以进行加、减计算,使用率较高的是点乘,点乘只发生在两个向量之间。
2个单位向量 点乘 得到 一个标量 --> 标量:没有方向,只有数值 --> 一个 [-1,1] 的值,这个值其实就是两个向量间夹⻆的 cos 值 -- 余弦值。
如何求2个普通向量的夹角呢?单位化向量 --> x,y,z 分别 ➗ 向量的模(x/|xyz|, y/|xyz|, z/|xyz|) --> 与此普通向量方向相同的单位向量。
2.1、向量的点乘
// math3d 库中提供了了关于点乘的API
// 1.m3dDotProduct3 函数获得2个向量之间的点乘结果
float m3dDotProduct3(const M3DVector3f u,const M3DVector3f v);
// 2.m3dGetAngleBetweenVector3 可获取2个向量之间夹角的弧度值
float m3dGetAngleBetweenVector3(const M3DVector3f u,const M3DVector3f v)
3、向量的叉乘(cross product)
2个向量v1、v2叉乘可得到一个向量v3,向量v3垂直于向量v1、v2 --> 法线 --> 游戏场景中
叉乘不满足交换律,因为向量是有方向的,交换叉乘方向会不同。
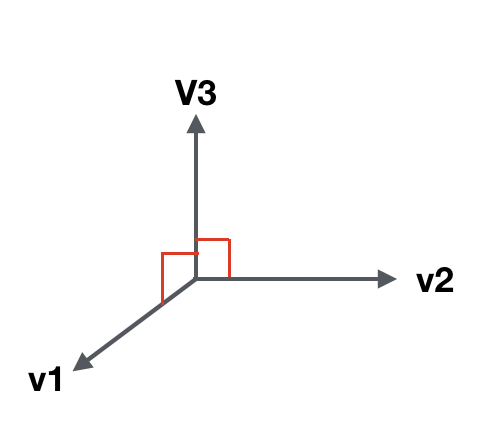
3.1、向量的叉乘
math3d 库中提供了关于叉乘的API // 1.m3dCrossProduct3 函数获得2个向量之间的叉乘结果 --> 一个新的向量 void m3dCrossProduct3(M3DVector3f result,const M3DVector3f u ,const M3DVector3f v);
二、矩阵(Matrix)
为什么使用矩阵?
我们对一个物体进行移动旋转等操作时,物体的每个点都需要进行相应的移动旋转,简单的图形的平移可以对每个点进行x,y,z的计算,但是当物体移动很复杂,顶点又很多时,我们对每个点进行计算操作再赋值的工作量很大且易出错,更何况有旋转时我们不一定精确知道角度,此时,矩阵就解决了我们的这个问题。
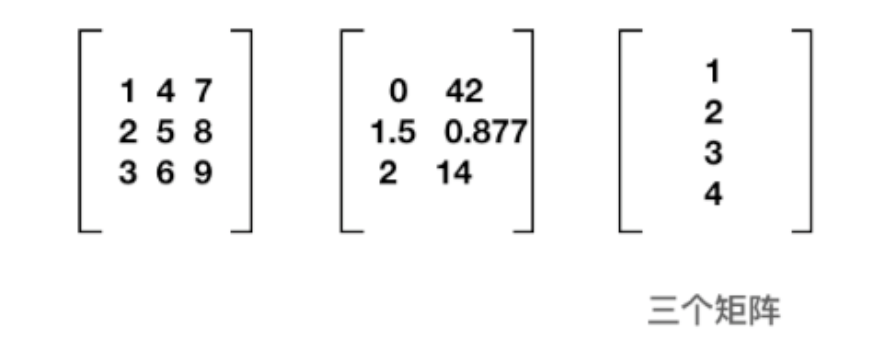
矩阵一行 or 一列都是合理的,其也可以称为向量。
1、矩阵的声明
// 三维矩阵/四维矩阵的声明
typedef float M3DMatrix33f[9];
typedef float M3DMatrix44f[16];
在其他编程标准中, 许多矩阵库定义一个矩阵时使⽤的是二维数组;
OpenGL 的约定里,更多倾向使⽤一维数组,这样做的原因是: OpenGL 使⽤的是 Column-Major (以列为主)矩阵排序的约定。 --> 列矩阵 == 转置矩阵(数学中的)

列优先矩阵:
下图,这 16 个值表示空间中一个特定的位置,这4列中,每⼀列都是有4个元素组成的向量;
如果无们要转动一个一个物体,那么将此物体所有的顶点向量 每一个顶点依次乘以一个矩阵,让此物体所有的顶点都应用 相同的变换,从而得到物体转动后 所在的空间中的 位置和⽅向。
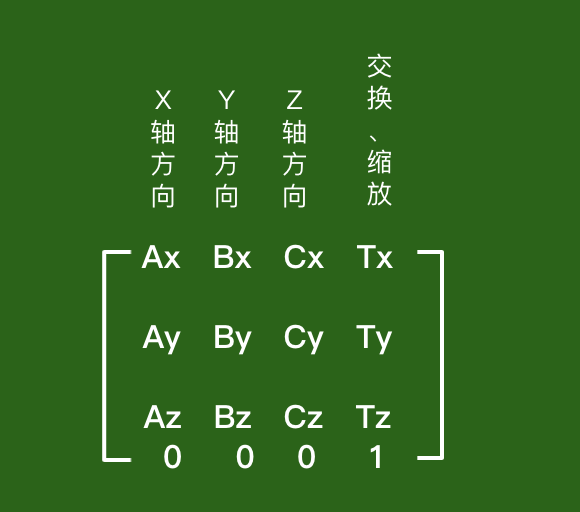
列向量的特别标注:矩阵的最后⼀行都为0,最后⼀个元素为0。
单元矩阵:
// 单元矩阵初始化 ⽅式1 GLFloat m[] = { 1,0,0,0, //X Column 0,1,0,0, //Y Column 0,0,1,0, //Z Column 0,0,0,1 // Translation } // 单元矩阵初始化 方式 2 M3DMatrix44f m = { 1,0,0,0, //X Column 0,1,0,0, //Y Column 0,0,1,0, //Z Column 0,0,0,1 // Translation }
// 单元矩阵初始化 方式3
void m3dLoadIdentity44f(M3DMatrix44f m);
2、矩阵的乘法
线性代数角度计算:线性代数中,为便于书写,坐标的 计算顺序都是从左到右的方式进行的。
变换后顶点向量 = V_local * M_model * M_view * M_pro
顶点 * 模型矩阵 * 视图矩阵 * 投影矩阵
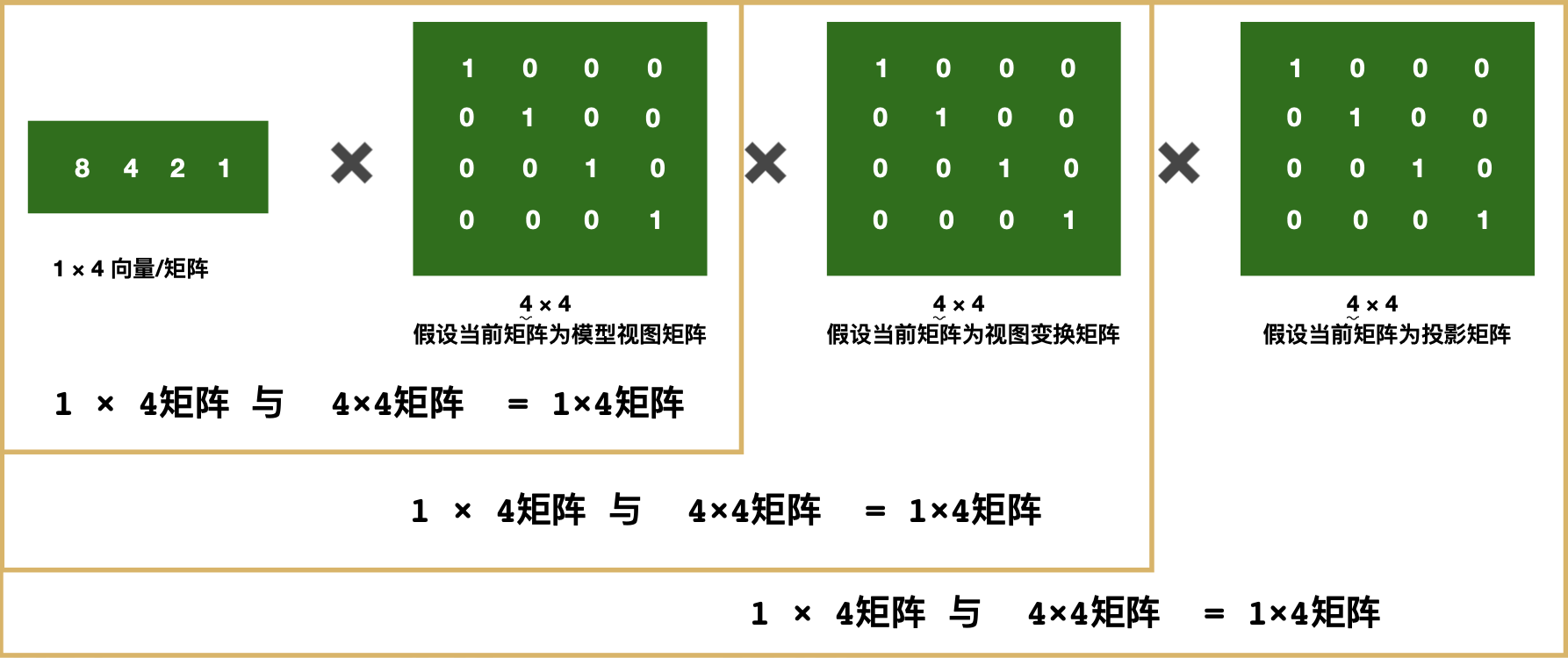
从OpenGL的角度:因为OpenGL中的约定是列优先矩阵,所以计算如下:
变换后顶点向量 = M_pro * M_view * M_model * V_local
投影矩阵 * 视图变换矩阵 * 模型矩阵 * 顶点
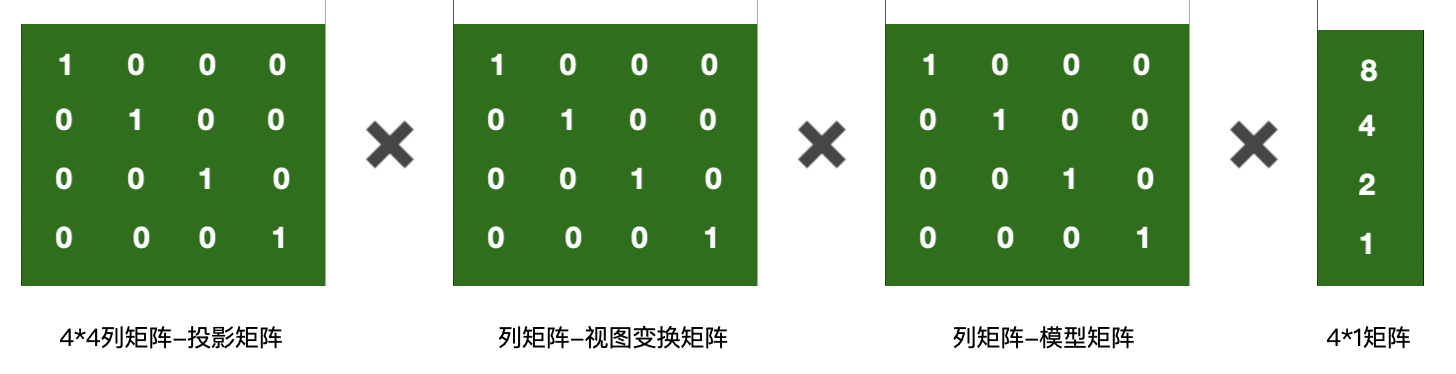
矩阵的计算规则:左乘:代数中,用到两个矩阵相乘的时候,矩阵A×矩阵B,那么就称为 A左乘以B。
三、OpenGL中的变换

1、视图变换
2个视角的 视觉坐标系
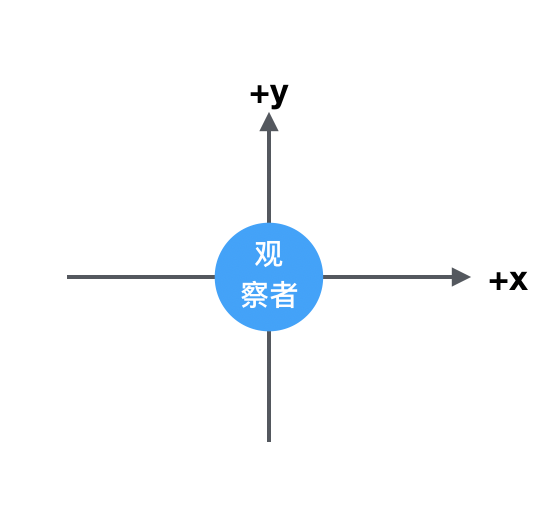
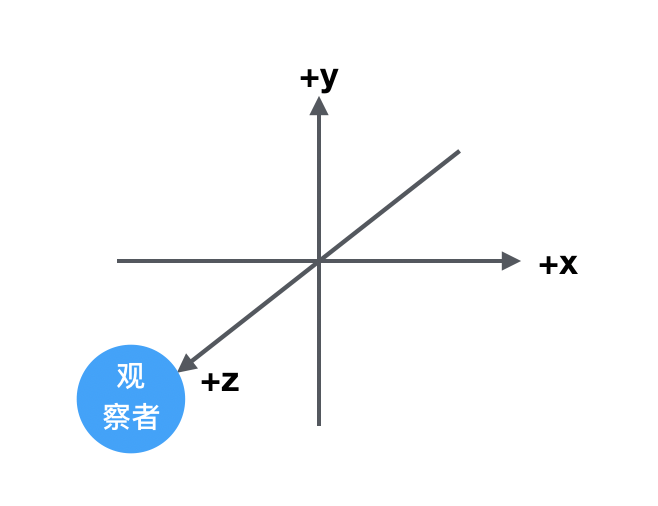
视图变换是应⽤到场景中的第⼀种变换, 它⽤来确定场景中的有利位置,在默认情况下, 透视投影中 位于原点(0,0,0),并沿着 z 轴负⽅向进⾏观察 (向显示器内部”看过去”)。当观察者点 位于原点(0,0,0) 时,就像在透视投影中⼀样。
视图变换将观察者放在你希望的任何位置,并允许在任何⽅向上观察场景, 确定视图变换就像 在场景中放置观察者并让它指向某⼀个⽅向;
从⼤局上考虑, 在应⽤任何其他模型变换之前, 必须先应⽤视图变换。这样做是因为, 对于视觉坐标系⽽言, 视图变换移动了当前的⼯作的坐标系; 后续的变化都会基于新调整的坐标系进⾏。 -- 《OpenGL超级宝典》
2、模型变换
⽤于操纵模型与其中某特定变换。这些变换通过 旋转,缩放,平移 将对象移动到需要的位置。模型变换的平移旋转缩放的不同顺序结果是不同的。
1.1 平移
void m3dTranslationMatrix44(M3DMatrix44f m, floata x, float y, float z);// M3DMatrix44f m 平移的结果
1.2 旋转
m3dRotationMatrix44(m3dDegToRad(45.0), floata x, float y, float z);// 有返回值
1.3 缩放
void m3dScaleMatrix44(M3DMatrix44f m, floata xScale, float yScale, float zScale);// M3DMatrix44f m 缩放的结果
1.4 综合变换 -- 既缩放也平移
void m3dMatrixMultiply44(M3DMatrix44f product, const M3DMatrix44f a, const M3DMatrix44f b); //M3DMatrix44f product放结果; const M3DMatrix44f a、b ,顺序不定,根据需求确定是 先平移还是先缩放。
3、投影变换
