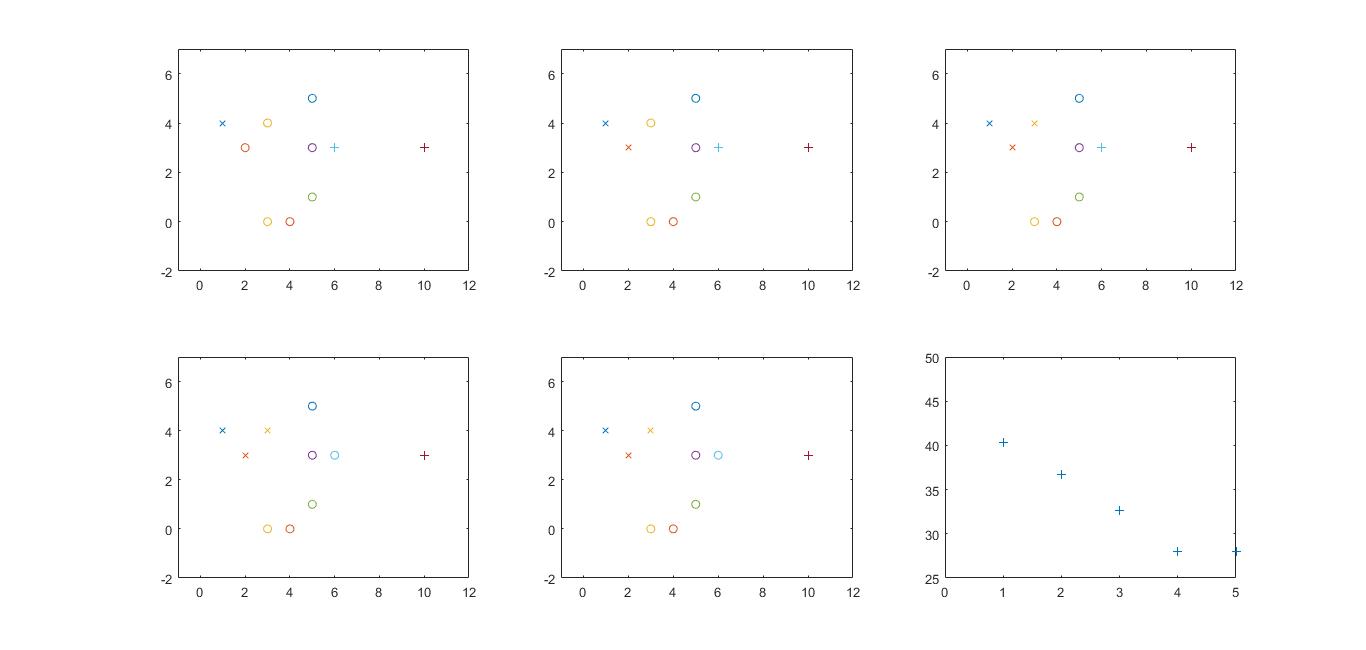
对散点进行二分聚类:
初始聚类中心的选择会影响分类次数甚至是否能成功分类, 算法采用离样本中心很近的两点作为初始聚类点.
程序如下:
% 设定分类次数,以自动调整分类精确度
% part1 得到散点数据并人工指定两个初始聚类中心点
clear all;clc;close all; %注意,3c前面不能写东西,会被擦除.
x = [ [1,4]; [2,3]; [3,4]; [5,3]; [5,1]; [6,3]; [10,3]; [5,5 ] ];
cluster_count = 4; % 聚类次数
len = size(x, 1);
intpx = 0;
intpy = 0;
for i = 1:len
intpx = intpx + x(i, 1);
intpy = intpy + x(i, 2);
end
intpx = intpx/len;
intpy = intpy/len;
% 注意坐标和矩阵要用方括号而不是圆括号
theta1 = [intpx + 0.01, intpy + 0.01];
theta2 = [intpx - 0.01, intpy - 0.01];
figure;
% part2 循环过程,其中,计数矩阵和索引矩阵的每次初始化都在循环中完成
for j = 1:cluster_count
% 初始化索引和计数矩阵
c = zeros(2, 1);
% 画聚类中心点, 中点, 求斜率画中垂线
subplot(2,2,j);
title(['di',num2str(j)]);
plot(theta1(1), theta1(2), '*'); hold on;
plot(theta2(1), theta2(2), '*'); hold on;
mid1 = (theta1(1) + theta2(1))/2;
mid2 = (theta1(2) + theta2(2))/2;
plot(mid1, mid2, '+'); hold on;
axis([-2 10 -2 10])
slope = (-1) * (theta1(1) - theta2(1))/(theta1(2) - theta2(2));
t = 0:0.01:10;
line = slope*(t-mid1) + mid2;
plot(t, line); hold on;
% 判断分类结果, 画出ox区分, 并得到新的双theta
% a 分类
thetanew1 = [0, 0]; thetanew2 = [0, 0];
for i = 1:len
if (x(i,1)-theta1(1))^2 + (x(i,2)-theta1(2))^2 < (x(i,1)-theta2(1))^2 + (x(i,2)-theta2(2))^2
y(i) = 1;
c(1) = c(1) + 1;
plot(x(i,1), x(i,2), 'x');hold on;
thetanew1(1) = thetanew1(1) + x(i,1);
thetanew1(2) = thetanew1(2) + x(i,2);
else
y(i) = 0;
c(2) = c(2) + 1;
plot(x(i,1), x(i, 2), 'o');hold on;
thetanew2(1) = thetanew2(1) + x(i,1);
thetanew2(2) = thetanew2(2) + x(i,2);
end
end
theta1 = thetanew1/c(1);
theta2 = thetanew2/c(2);
% b 双theta
axis([-2 10 -2 10])
end
% 若第一次分类为初始值分类,则可见第三次分类已达最佳
输出图像如下:
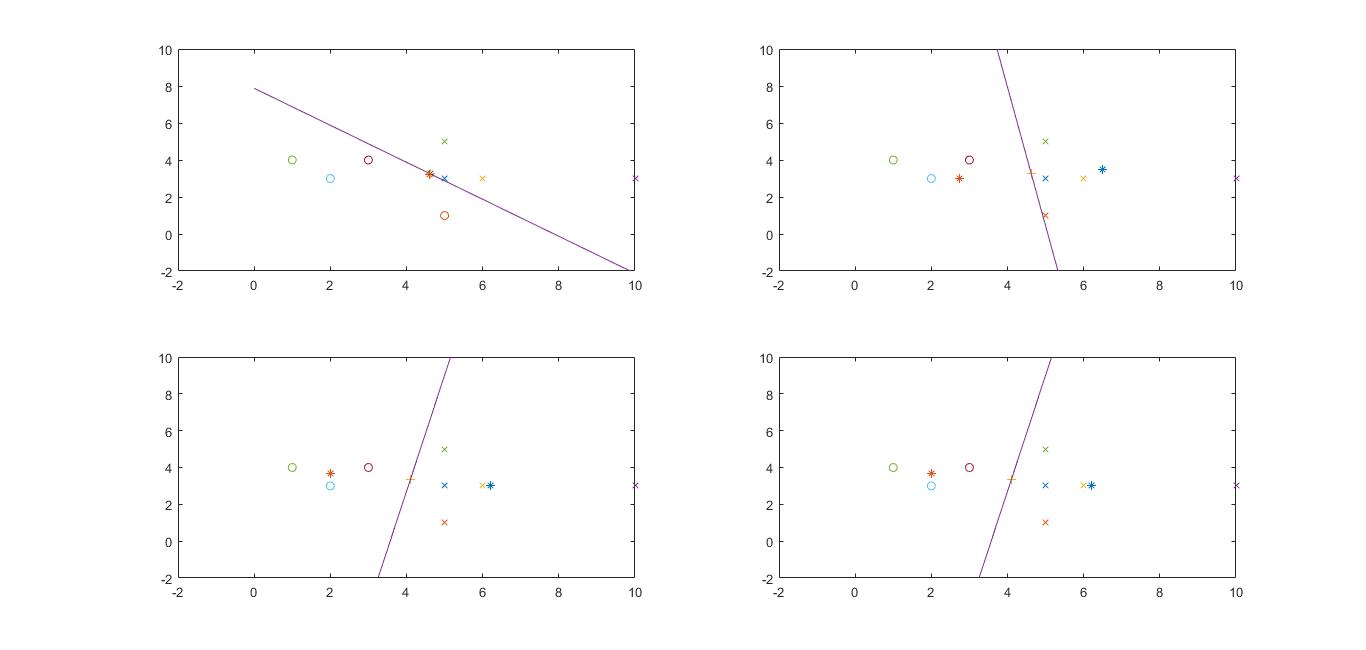
三分聚类:
% 三分聚类
% 2c
clc; close all;
% clear all is not really necesssary, beccause every variable with the same
% name
% 导入要分类的散点数据
x = [ [1,4]; [2,3]; [3,4]; [5,3]; [5,1]; [6,3]; [10,3]; [5,5 ]; [4, 0]; [3, 0] ];
%x = [ [1, 1]; [2, 1]; [2,2]; [8,1]; [8,2]; [8,3]; [4, 8]; [5, 8] ];
cluster_times = 4;
len = size(x, 1);
xxall = 0; xyall = 0;
for i = 1:len
xxall = xxall + x(i, 1);
xyall = xyall + x(i, 2);
end
xysum = [xxall, xyall];
intpx = 0;
intpy = 0;
for i = 1:len
intpx = intpx + x(i, 1);
intpy = intpy + x(i, 2);
end
intpx = intpx/len;
intpy = intpy/len;
% 注意坐标和矩阵要用方括号而不是圆括号
%{
theta1 = [intpx, intpy + 1.01];
theta2 = [intpx - 1.02, intpy + 1.03];
theta3 = [intpx + 1.04, intpy - 1.05];
%}
theta1 = x(1,:);
theta2 = x(2,:);
theta3 = x(10,:);
% 判断
for j = 1:cluster_times
% 初始化索引和计数矩阵
c = zeros(3, 1);
% 画聚类中心点, 中点, 求斜率画中垂线
%subplot(3,3,j);
figure;
% title(['di',num2str(j)]);
% plot(mid1, mid2, '+'); hold on;
axis([-2 10 -2 10])
% 判断分类结果, 画出ox区分, 并得到新的双theta
% a 分类
thetanew1 = [0, 0]; thetanew2 = [0, 0]; thetanew3 = [0, 0];
for i = 1:len
if (x(i,1)-theta1(1))^2 + (x(i,2)-theta1(2))^2 < (x(i,1)-theta2(1))^2 + (x(i,2)-theta2(2))^2 ...
&& ((x(i,1)-theta1(1))^2 + (x(i,2)-theta1(2))^2 < (x(i,1)-theta3(1))^2 + (x(i,2)-theta3(2))^2)
y(i) = 0;
c(1) = c(1) + 1;
plot(x(i,1), x(i,2), 'x');hold on;
thetanew1(1) = thetanew1(1) + x(i,1);
thetanew1(2) = thetanew1(2) + x(i,2);
elseif (x(i,1)-theta2(1))^2 + (x(i,2)-theta2(2))^2 < (x(i,1)-theta1(1))^2 + (x(i,2)-theta1(2))^2 ...
&& ((x(i,1)-theta2(1))^2 + (x(i,2)-theta2(2))^2 < (x(i,1)-theta3(1))^2 + (x(i,2)-theta3(2))^2)
y(i) = 1;
c(2) = c(2) + 1;
plot(x(i,1), x(i, 2), 'o'); hold on;
thetanew2(1) = thetanew2(1) + x(i,1);
thetanew2(2) = thetanew2(2) + x(i,2);
else
y(i) = 2;
c(3) = c(3) + 1;
plot(x(i, 1), x(i, 2), '+'); hold on;
thetanew3(1) = thetanew3(1) + x(i, 1);
thetanew3(2) = thetanew3(2) + x(i, 2);
end
end
theta1 = thetanew1/c(1);
theta2 = thetanew2/c(2);
theta3 = thetanew3/c(3);
mid12 = (theta1 + theta2)/2;
mid23 = (theta2 + theta3)/2;
mid31 = (theta3 + theta1)/2;
slope12 = (-1) * (theta1(1) - theta2(1))/(theta1(2) - theta2(2)); %负倒数通过交换分子分母得到
slope23 = (-1) * (theta2(1) - theta3(1))/(theta2(2) - theta3(2));
slope31 = (-1) * (theta3(1) - theta1(1))/(theta3(2) - theta1(2));
t = 0:0.01:10;
%t = 4.2:0.01:10;
line12 = slope12*(t-mid12(1)) + mid12(2);
plot(t, line12); hold on;
%t = 0:0.01:4.2;
line23 = slope23*(t-mid23(1)) + mid23(2);
plot(t, line23); hold on;
%t = 4.2:0.01:10;
line31 = slope31*(t-mid31(1)) + mid31(2);
plot(t, line31); hold on;
%plot(theta1(1), theta1(2), '*');
%plot(theta2(1), theta2(2), '*');
%plot(theta3(1), theta3(2), '*');
% 运行结果不能达到预期时先不要否定算法而是先检查一下细节
% b 双theta
axis([-2 10 -2 10])
end
输出如下:
初始点theta1, theta2, theta3 选x1, x2, x10:
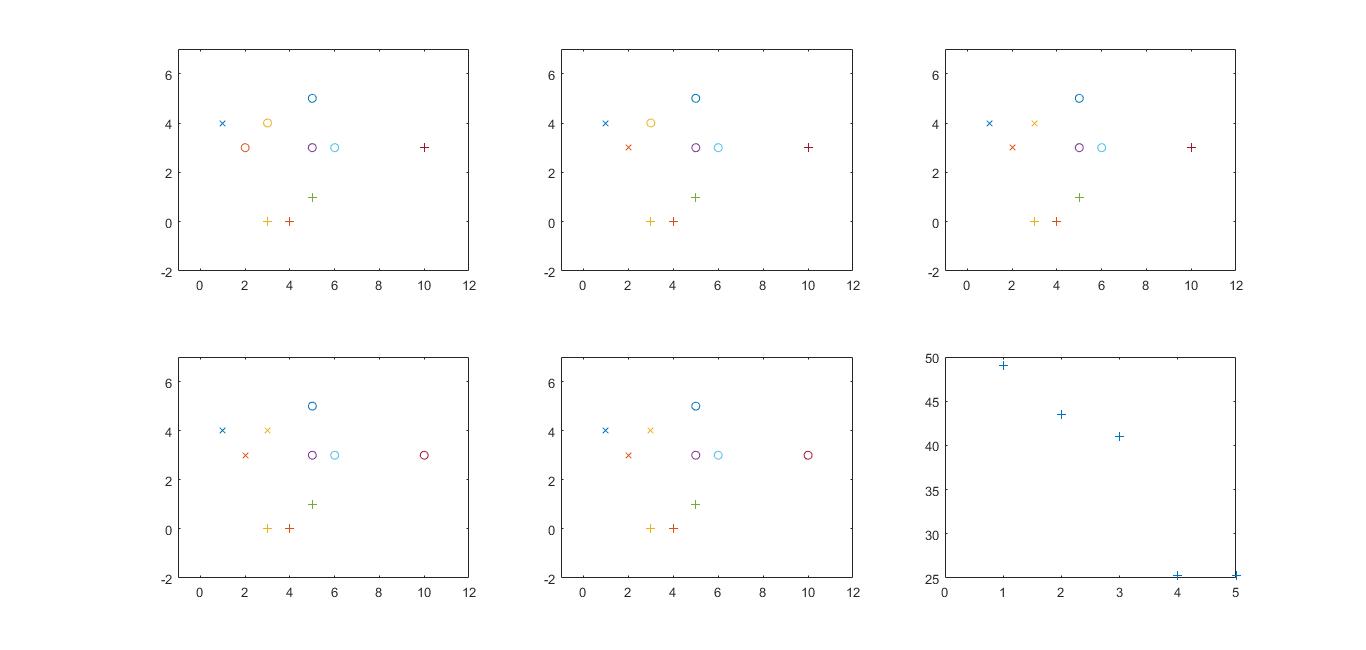
初始点选x1, x2, x7 就会陷入局部最优: