202006-1 线性分类器
题目描述
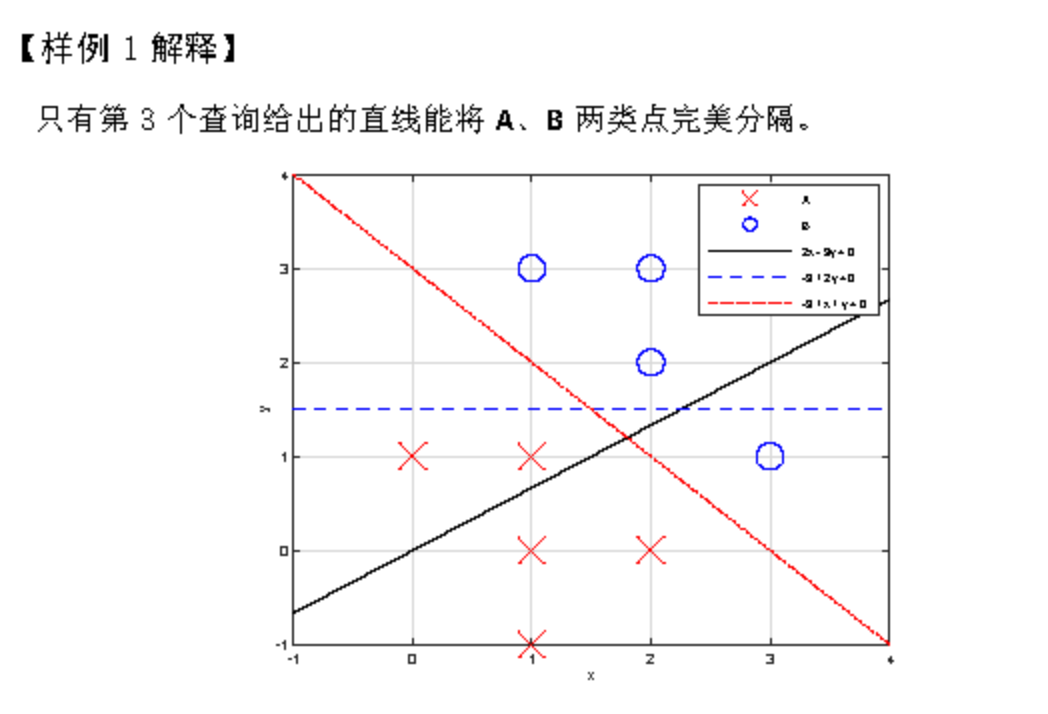
考虑一个简单的二分类问题——将二维平面上的点分为A和B两类。
训练数据包含n个点,其中第i个点(\(1\le i \le n\))可以表示为一个三元组(\(x_i,y_i,type_i\)),即该点的横坐标、纵坐标和类别。
在二维平面上,任意一条直线可以表示为\(\theta_0+\theta_1x+\theta_2y=0\)的形式,即由\(\theta_0、\theta_1\)和\(\theta_2\)三个参数确定该直线,且满足\(\theta_1、\theta_2\)不同时为0。
基于这n个已知类别的点,我们想要在平面上找到一条直线作为一个线性分类器。具体来说,这条线要把训练数据中的A、B两类点完美分隔开来,即一侧只有A类点、另一类只有B类点。这样,对于任意一个的未知类别的点,我们就可以根据它是位于直线的哪一侧来预测它的类别了。
在本题中我们仅需要处理m个如下查询:给定一条直线,判断它是否能将训练数据中的A、B两类点完美分开。
输入格式
从标准输入读入数据。
输入共\(n+m+1\)行。
第一行包含用空格分隔的两个正整数\(n\)和\(m\),分别表示点和查询的个数。
第二行到第\(n+1\)行依次输入\(n\)个点的信息。第\(i+1\)行(\(1\le i \le n\))包含用空格分隔的三项\(x_i\)、\(y_i\)和\(type_i\),分别表示第\(i\)个点的横、纵坐标和类别,其中坐标为整数、类别为一个大写英文字母\(A\)和\(B\)。
第\(n+2\)行到第\(n+m+1\)行依次输入\(m\)个查询。第\(j+n+1\)行(\(1\le j \le m\))包含用空格分隔的三个整数\(\theta_0、\theta_1\)和\(\theta_2\),表示第\(j\)个查询中给定直线的三个参数。
输出格式
输出到标准输出。
输出到\(m\)行,每行输出一个字符串。
第\(j\)行(\(1\le j \le m\))输出的字符串对应第\(j\)个查询的结果:如果给定直线可以完美分隔A、B两类点,则输出Yes;否则输出No。
样例输入1
9 3
1 1 A
1 0 A
1 -1 A
2 2 B
2 3 B
0 1 A
3 1 B
1 3 B
2 0 A
0 2 -3
-3 0 2
-3 1 1
样例输出1
No
No
Yes
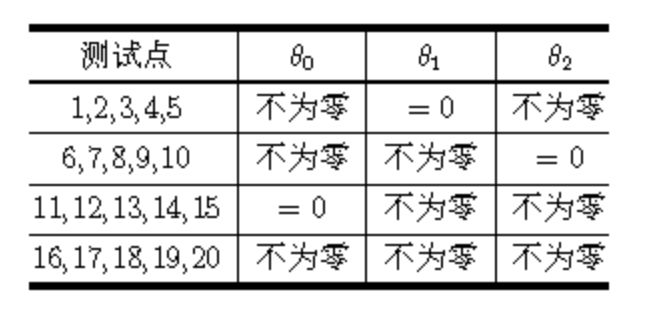
子任务
- 输入数据保证不存在恰好落在给定直线上的点;
- \(0 \lt n \le 10^3\)、\(0\lt m \le 20\),且A、B两类点的数量均不为0;
- 所有点的坐标和给定直线的三个参数均为整数,且绝对值\(\le10^6\);
- 任意两个点的坐标不完全相同。
代码
#include <stdio.h>
struct Node {
int x;
int y;
char kind;
}node[1000];
int Check(int n,int x0,int x1,int x2) {
char kind_first = 'a', kind_second = 'b';
int i;
for (i = 0; i < n; ++i) {
int result=x0 + node[i].x * x1 + node[i].y * x2;
if (result== 0)
return 0;
if (result > 0) {
kind_first = node[i].kind;
}
else if (result < 0) {
kind_second = node[i].kind;
}
if (kind_first == kind_second)
return 0;
}
return 1;
}
int main()
{
int n, m;
int x0, x1, x2;
scanf("%d %d",&n,&m);
int i;
for ( i= 0; i < n; ++i)
{
scanf("%d %d %c", &node[i].x, &node[i].y ,&node[i].kind);
}
int ans[20];
for ( i = 0; i < m; ++i) {
scanf("%d %d %d", &x0, &x1 ,&x2);
ans[i]=Check(n,x0,x1,x2);
}
for(i =0 ;i<m;i++){
if (ans[i]) {
printf("Yes\n");
}
else
printf("No\n");
}
return 0;
}