题目描述:

输入输出:

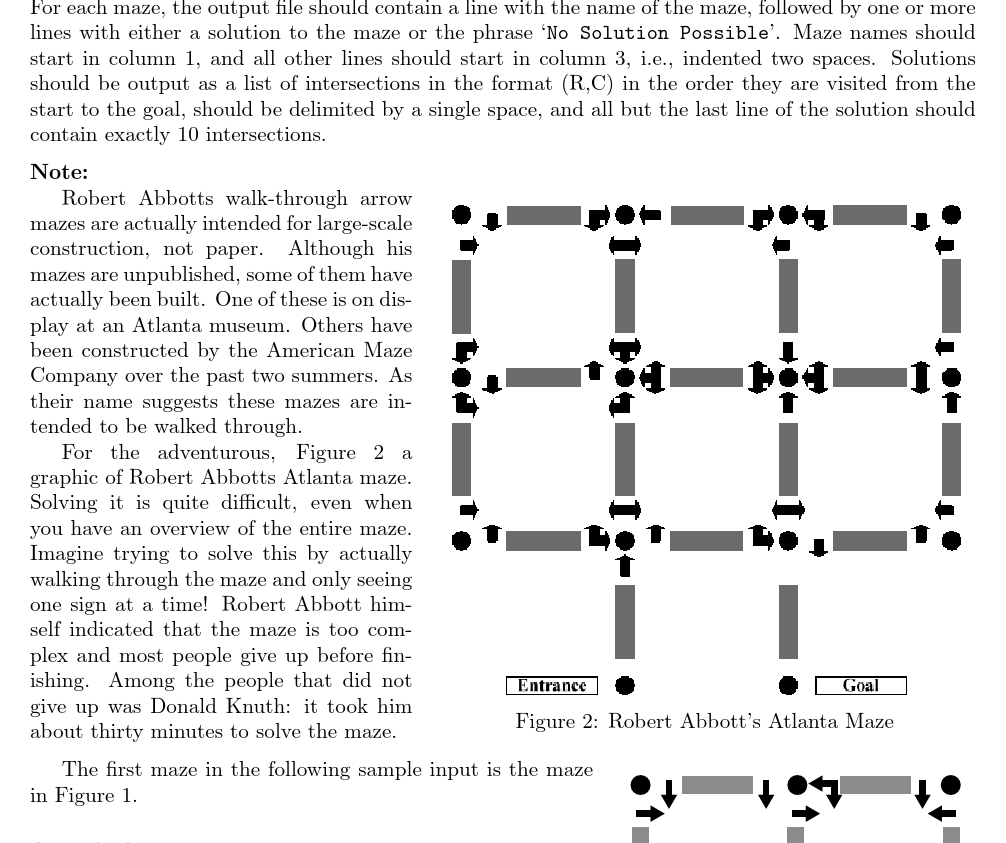
输入样例:
SAMPLE
3 1 N 3 3
1 1 WL NR *
1 2 WLF NR ER *
1 3 NL ER *
2 1 SL WR NF *
2 2 SL WF ELF *
2 3 SFR EL *
0
NOSOLUTION
3 1 N 3 2
1 1 WL NR *
1 2 NL ER *
2 1 SL WR NFR *
2 2 SR EL *
0
END
输出样例:
SAMPLE
(3,1) (2,1) (1,1) (1,2) (2,2) (2,3) (1,3) (1,2) (1,1) (2,1)
(2,2) (1,2) (1,3) (2,3) (3,3)
NOSOLUTION
No Solution Possible
思路:
将普通图(只含有两个方向的平面图)改为三元组表示的图,再在“平面图”的基础上调用BFS算法,求单元最短路径。输入输出很繁(对我这个菜鸡来说)。
还有就是行走函数根据转向不同将char类型的方向映射到两个一维的int上去的方式很巧妙(巧妙的加3加1取余4,就打乱原来的NESW逆时针顺序),
再通过dr,dc数组实现方向的变化和移动。注意初始位置(r1,c1)不是原始位置(r0,c0)。
开始将d数组初始化为-1,到d[r1][c1][dir]就为0(加了1)。所以在用vector反着打印路径时最后加一个(r0,c0)(未存)
代码:(有详细的但也难懂的注释)
1 #include <cstdio>
2 #include <iostream>
3 #include <cstring>
4 #include <vector>
5 #include <queue>
6 #define max_n 10
7 using namespace std;
8 struct Node
9 {
10 int r;
11 int c;
12 int dir;
13 Node(int r1=0,int c1=0,int d1=0) :r(r1),c(c1),dir(d1) {}
14 //构造Node,带有默认参数,不然会在Node p[][][]那里报错,认为这个语句是在构造Node
15 };
16 int d[max_n][max_n][4];//表示初始状态到(r,c,dir)的最短路长度
17 Node p[max_n][max_n][4];//保存了状态(r,c,dir)在BFS数中的父结点
18 int has_edge[max_n][max_n][4][3];//当前状态是(r,c,dir),是否可以沿着转弯方向turn行走
19
20 //行走
21 const char* dirs = "NESW"; //顺时针旋转的顺序
22 const char* turns = "FLR";
23 int dir_id(char c) {return strchr(dirs,c)-dirs;} //将char类型的dir转化为dirs中相应的所在位置
24 int turn_id(char c) {return strchr(turns,c)-turns;}//将char类型的turn在turns中找到对应的元素位置
25 const int dr[] = {-1,0,1,0};//用上面找到的元素位置来确定当前行行走方向
26 const int dc[] = {0,1,0,-1};//用上面找到的元素位置来确定当前列行走方向
27 char maze[21];//迷宫名称
28 int r0,c0,dir;//原始位置和方向
29 int r1,c1;//初始位置和方向
30 int r2,c2;//目标位置
31 //巧妙的行走函数和对应关系
32 //dirs 0N 1E 2S 3W
33 //顺时针
34 //dir' 3 0 1 2
35 //逆时针
36 //dir' 1 2 3 0
37 //dr -1 0 1 0
38 //dc 0 1 0 -1
39 Node walk(const Node& u,int turn)
40 {
41 int dir = u.dir;
42 if(turn==1) dir = (dir+3)%4;
43 if(turn==2) dir = (dir+1)%4;
44 return Node(u.r+dr[dir],u.c+dc[dir],dir);
45 }
46 //判断越界函数
47 int inside(int r,int c)
48 {
49 return 0<r&&r<=9&&0<c&&c<=9;
50 }
51 //输出函数
52 //要求:
53 //第一行输出迷宫名
54 //后几行输出路径,且除最后一行外,其他每行都是空两格+10个(r,c)形式空格分隔的坐标
55 void printa(Node u)
56 {
57 vector<Node> nodes;//可用递归方式打印,但可能溢栈,可改用循环,用vector存储
58 for(;;)
59 {
60 nodes.push_back(u);
61 if(d[u.r][u.c][u.dir]==0) break;
62 u = p[u.r][u.c][u.dir];
63 }
64 nodes.push_back(Node(r0,c0,dir));
65
66 int cnt = 0;
67 for(int i = nodes.size()-1;i>=0;i--)
68 {
69 if(cnt%10==0) //值得品味的细节1
70 {
71 printf(" ");
72 }
73 printf(" (%d,%d)",nodes[i].r,nodes[i].c);
74 if(++cnt%10==0)//值得品味的细节2
75 {
76 printf("
");
77 }
78 }
79 if(nodes.size()%10!=0)
80 {
81 printf("
");
82 }
83 }
84 //输入函数
85 //先读入迷宫名,若为END返回0,
86 //然后一行读入起点r,c,dir,终点r,c
87 //然后处理交叉处的方向改变,将这些信息用数组has_edge[r][c][dir][turn]记录下来,为以后BFS提供基础
88 //读到*结束小循环,读到0结束大循环
89 int read()
90 {
91 cin >> maze;
92 if(maze[0]=='E'&&maze[1]=='N'&&maze[2]=='D'&&strlen(maze)==3) return 0;
93 cout << maze << endl;
94 memset(maze,0,sizeof(maze[0]));
95
96 char dirs;
97 cin >> r0 >> c0 >> dirs >> r2 >> c2;
98 dir = dir_id(dirs);
99 r1 = r0+dr[dir];
100 c1 = c0+dc[dir];
101 memset(has_edge,0,sizeof(has_edge));
102
103 for(;;)
104 {
105 int r,c;
106 cin >> r;
107 if(r==0)
108 {
109 break;
110 }
111 cin >> c;
112 char chr[99];
113 while(cin >> chr)
114 {
115 if(chr[0]=='*')
116 {
117 break;
118 }
119 for(int i = 1;i<strlen(chr);i++)
120 {
121 has_edge[r][c][dir_id(chr[0])][turn_id(chr[i])] = 1;
122 }
123 //cout << r << " " << c << " " << chr << endl;
124 memset(chr,0,sizeof(chr[0]));
125 }
126 }
127 return true;
128 }
129 //BFS主过程
130 void solve()
131 {
132 queue<Node>q;
133 memset(d,-1,sizeof(d));
134 Node u(r1,c1,dir);
135 d[u.r][u.c][u.dir] = 0;
136 q.push(u);
137 while(!q.empty())
138 {
139 Node u = q.front();q.pop();
140 if(u.r==r2&&u.c==c2)
141 {
142 printa(u);
143 return;
144 }
145 for(int i = 0;i<3;i++)
146 {
147 Node v = walk(u,i);
148 if(has_edge[u.r][u.c][u.dir][i]&&inside(v.r,v.c)&&d[v.r][v.c][v.dir]<0)
149 {
150 d[v.r][v.c][v.dir] = d[u.r][u.c][u.dir] +1;
151 p[v.r][v.c][v.dir] = u;
152 q.push(v);
153 }
154
155 }
156 }
157 printf(" No Solution Possible
");
158 }
159 int main()
160 {
161 while(read())
162 solve();
163 return 0;
164 }


