二叉搜索树
/**
* 二叉搜索树
*/
public class BinarySearchTree {
public BinaryTreeNode<Integer> root;
public int size;
public BinarySearchTree() {
this.size = 0;
}
//所谓生成二叉搜索树,就是通过n次的插入结点来完成
public BinaryTreeNode generateBST(int[] arr){
BinarySearchTree tree = new BinarySearchTree();
BinaryTreeNode tmp = tree.root;
tmp = insertNode(tmp,arr[0]); //生成根节点,要接收新的引用
for(int i=1;i<arr.length;i++){ //从1开始
insertNode(tmp,arr[i]);
}
return tmp;
}
//二叉搜索树的插入 (整形的插入测试)
public BinaryTreeNode insertNode(BinaryTreeNode node,int value){
if(node==null){ //插入根节点
node = new BinaryTreeNode(value);
return node; //返回新的引用
}
//插入的值比当前子树的根结点要小(等),往左走
//(且要判断左孩子是否为空,为空就表示可以直接插入---因为没有左孩子,就没有比他更小的了)
if(value<=(Integer) node.data&&node.lchild!=null){
insertNode(node.lchild,value);
}else {
//说明左孩子为null
if(value<=(Integer)node.data){
node.insertLeft(value); //插入左孩子
}else if(value>(Integer)node.data&&node.rchild!=null){
insertNode(node.rchild,value);
}else{
//说明右孩子为null
node.insertRight(value); //插入右孩子
}
}
return null;
}
//层序遍历
public void levelTraverse() throws Exception {
BinaryTreeNode node = root;
CycleQueue queue = new CycleQueue(new BinaryTreeNode[100]);
queue.enQueue(node);
while (!queue.isEmpty()){
BinaryTreeNode current = (BinaryTreeNode) queue.deQueue();
System.out.printf("%5d",current.data);
if(current.lchild!=null){
queue.enQueue(current.lchild);
}
if(current.rchild!=null){
queue.enQueue(current.rchild);
}
}
}
}
测试:
/**
* 二叉搜索树
*/
BinarySearchTree searchTree = new BinarySearchTree();
int array[] = {50,24,76,4,32,64,100};
int array2[] = {20,40,10,80,45,60,12};
searchTree.root = searchTree.generateBST(array2);
System.out.println();
System.out.println("层序遍历二叉搜索树:");
searchTree.levelTraverse();
}
总结:
简单来说:从根节点出发,往哪里走的问题
插入结点,生成树其实就是不断的插入而成
loop(node,value):
- 当比根节点大(往右走)
- 往右走如果右孩子为空,则直接插入作为右孩子
- 如果右孩子不为空,则递归进右孩子处goto loop(node.rchild,value)。继续做根节点的左右大小比较(决定往哪走)
- 比根节点小(往左走)
- 往左走若左孩子为空,则直接插入作为左孩子
- 如果左孩子不为空,则递归进左孩子goto loop(node.lchild,value)处。把这个左孩子当作根节点,继续做左右大小比较(决定下一步往哪走)
查找操作
//二叉搜索树的结点查找,判断是否存在
public boolean findNode(BinaryTreeNode node,int value){
//比node.data小,往左走,且判断左孩子是否为空
if(value<(Integer)node.data&&node.lchild!=null){
return findNode(node.lchild,value);
//表示由于左孩子为空而退出的if,且value仍然<node.data,所以表示找不到指定结点
}else if(value<(Integer)node.data){
return false;
}else if(value>(Integer)node.data&&node.rchild!=null){
return findNode(node.rchild,value);
}else if(value>(Integer)node.data){
return false;
}else{
//当上面的情况都不符合,就表示属于value==node.data的情况,所以表示找到了,返回true
return true;
}
}
时间复杂度:O(log2n)
删除操作
分析:
删除操作分三种情况
- 删除的结点无左,右孩子------可直接删除该结点(比如parent.lchild=null即可,java中无需手动释放资源,C和python都要释放)
- 删除的结点只有左或者右孩子中的一个---------首先判断删除节点是来自父节点的左孩子,还是右孩子。
- 被删除的结点A是左孩子,且A结点只有左孩子,那么--- parent.lchild = A.lchild
- 如果被删除结点B是右孩子,且B结点只有右孩子,那么---parent.rchild = B.rchild
- 删除的结点既有左孩子,又有右孩子-----做法是找到被删除的结点C,的右子树中最小的结点值min_value
- C.value = min_value 替换值
- 根据这个min_value 在C.rchild为根结点的子树中,删除(这个删除也就是我们定义的删除操作,递归式的)这个min_value所在的结点
//二叉搜索树的删除指定结点
public boolean deleteNode(BinaryTreeNode node,int value,BinaryTreeNode parent){
/**
* 首先找出该结点以及记录下他的双亲节点parent
* 1. 第一种情况:为叶子节点, 通过parent直接删除该节点即可 parent.lchild = null
* 2. 第二种情况,删除的结点有左孩子,或者右孩子,通过 如parent,parent.lchild = node.lchild,删除
* 3. 第三种情况,删除的结点有左孩子,也有右孩子,通过找到这个结点右子树中最小的结点(find_right_min)替代掉被删除的结点,且这个最小的结点要置为null
*/
if(value<(Integer)node.data&&node.lchild!=null){
return deleteNode(node.lchild,value,node);
}else if(value<(Integer)node.data){
return false; //表示没有这个结点
}else if(value>(Integer)node.data&&node.rchild!=null){
return deleteNode(node.rchild,value,node);
}else if(value>(Integer)node.data){
return false;
}else{
//表示value == node.data,存在该结点
//1. 左右孩子都不存在
if(node.lchild==null&&node.rchild==null){
//1.1 被删除节点是父节点的左孩子
if(node==parent.lchild){
parent.lchild = null;
return true;
//1.2 被删除节点是父节点的右孩子
}else{
parent.rchild = null;
return true;
}
//2. 左孩子存在,右孩子不在
}else if(node.lchild!=null&&node.rchild==null){
//2.1 当前结点是父节点的左孩子
if(node==parent.lchild){
parent.lchild = node.lchild;
return true;
//2.2 当前节点是父节点的右孩子
}else{
parent.rchild = node.lchild;
return true;
}
//3. 右孩子存在,左孩子不在
}else if(node.lchild==null&&node.rchild!=null){
//2.1 当前结点是父节点的左孩子
if(node==parent.lchild){
parent.lchild = node.rchild;
return true;
//2.2 当前结点是父节点的右孩子
}else{
parent.rchild = node.rchild;
return true;
}
//4. 左孩子,右孩子都在 node.lchild!=null&&node.rchild!=null
}else{
//4.1 找到右子树中最小的结点值
Integer min_value = find_min_value(node.rchild);
//4.2 替换最小值
node.data = min_value;
//4.3 删除右子树中的最小节点
deleteNode(node.rchild,min_value,node);
return true;
}
}
}
查找最小值
//内部方法,用于查找最小结点值
private Integer find_min_value(BinaryTreeNode node){
if(node==null){
return null;
}
if(node.lchild==null){
return (Integer)node.data;
}else{
return find_min_value(node.lchild);
}
}
测试:
int array3[] = {50,30,80,20,35,70,100,34,40,75,32,36};
BinarySearchTree st = new BinarySearchTree();
//注意,一定要接收这个返回的副本引用!!!
st.root = st.generateBST(array3);
System.out.println();
System.out.println("bst:");
st.levelTraverse();
//测试删除结点
System.out.println();
System.out.println("删除35结点: ");
st.deleteNode(st.root,35,st.root);
st.levelTraverse();
测试结果:
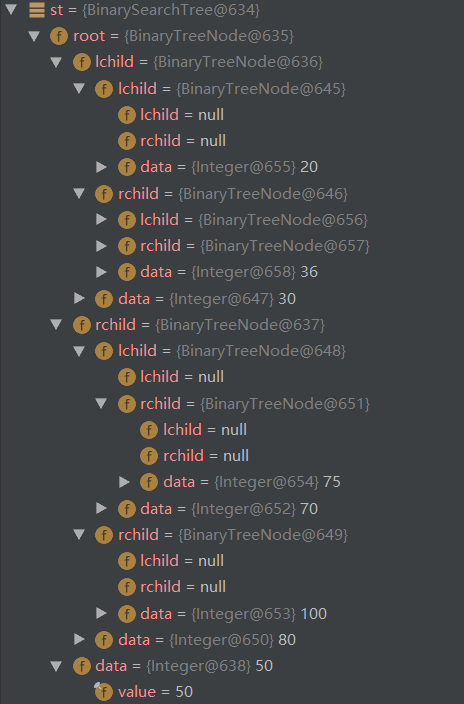
原树:
删除35后:
50
30 80
20 36 70 100
34 40 75
32