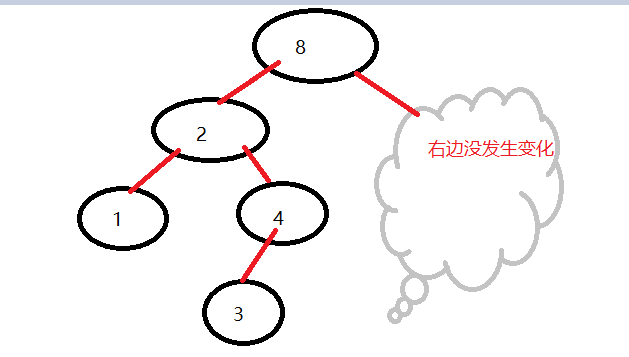
二叉平衡树
全图基础解释参考链接:http://btechsmartclass.com/data_structures/avl-trees.html
二叉平衡树:https://www.cnblogs.com/zhuwbox/p/3636783.html
前提:会写 求二叉树的深度
背景知识:
为什么需要二叉平衡树
答:因为二叉搜索树在理想状态下(也就是平衡树),查找的时间复杂度为log2n ,但是如果很不幸,
插入的数据都是有序数据的话,那么会退化成O(n)的线性时间复杂度。因为几乎退化成了链!
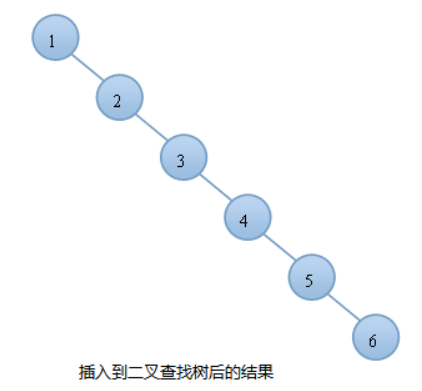
线性:6次
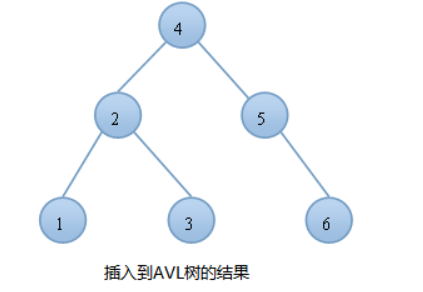
平衡:3次 log6+1 = 3
总结:树的基本操作的时间复杂度几乎都与树的高度有关,那么减少树的高度,就可以降低查询的时间复杂度。
我们知道,对于一般的二叉搜索树(Binary Search Tree),其期望高度(即为一棵平衡树时)为log2n,其各操作的时间复杂度(O(log2n))同时也由此而决定。但是,在某些极端的情况下(如在插入的序列是有序的时),二叉搜索树将退化成近似链或链,此时,其操作的时间复杂度将退化成线性的,即O(n)。我们可以通过随机化建立二叉搜索树来尽量的避免这种情况,但是在进行了多次的操作之后,由于在删除时,我们总是选择将待删除节点的后继代替它本身,这样就会造成总是右边的节点数目减少,以至于树向左偏沉。这同时也会造成树的平衡性受到破坏,提高它的操作的时间复杂度。
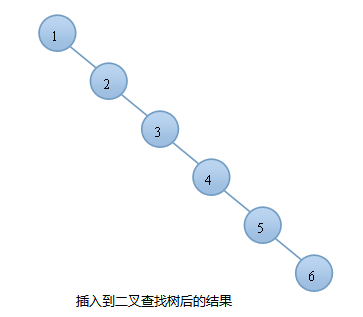
例如:我们按顺序将一组数据1,2,3,4,5,6分别插入到一颗空二叉查找树和AVL树中,插入的结果如下图:
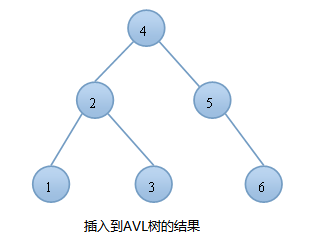
AVL树的插入
由上图可知,同样的结点,由于插入方式不同导致树的高度也有所不同。特别是在带插入结点个数很多且正序的情况下,会导致二叉树的高度是O(N),而AVL树就不会出现这种情况,树的高度始终是O(lgN).高度越小,对树的一些基本操作的时间复杂度就会越小。这也就是我们引入AVL树的原因
AVL树的操作基本和二叉查找树一样,这里我们关注的是两个变化很大的操作:插入和删除!
我们知道,AVL树不仅是一颗二叉查找树,它还有其他的性质。如果我们按照一般的二叉查找树的插入方式可能会破坏AVL树的平衡性。同理,在删除的时候也有可能会破坏树的平衡性,所以我们要做一些特殊的处理,包括:单旋转和双旋转!
AVL树的插入,单旋转的第一种情况---右旋:
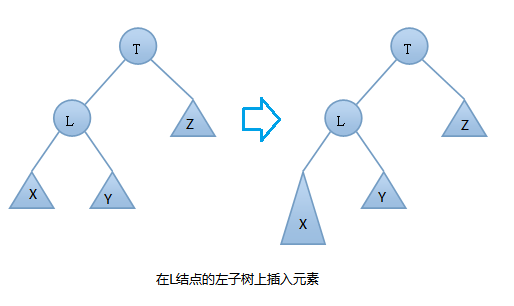
由上图可知:在插入之前树是一颗AVL树,而插入之后结点T的左右子树高度差的绝对值不再 < 1,此时AVL树的平衡性被破坏,我们要对其进行旋转。由上图可知我们是在结点T的左结点的左子树上做了插入元素的操作,我们称这种情况为左左情况,我们应该进行右旋转(只需旋转一次,故是单旋转)。具体旋转步骤是:
T向右旋转成为L的右结点,同时,Y放到T的左孩子上。这样即可得到一颗新的AVL树,旋转过程图如下:
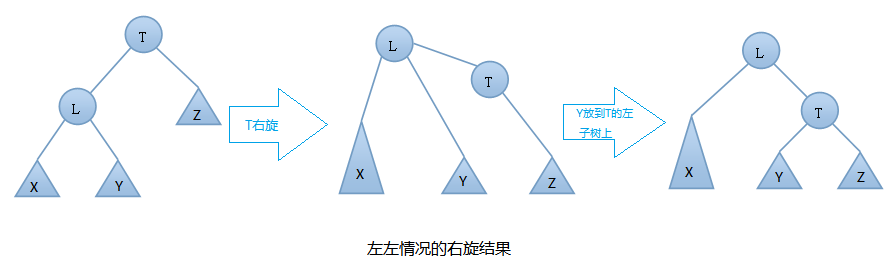
左左情况的右旋举例:
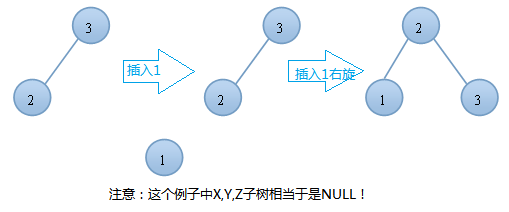
AVL树的插入,单旋转的第一种情况---左旋:
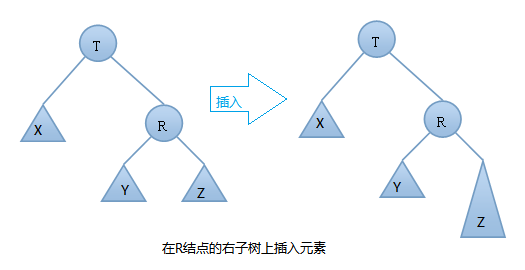
由上图可知:在插入之前树是一颗AVL树,而插入之后结点T的左右子树高度差的绝对值不再 < 1,此时AVL树的平衡性被破坏,我们要对其进行旋转。由上图可知我们是在结点T的右结点的右子树上做了插入元素的操作,我们称这种情况为右右情况,我们应该进行左旋转(只需旋转一次,故事单旋转)。具体旋转步骤是:
T向右旋转成为R的左结点,同时,Y放到T的左孩子上。这样即可得到一颗新的AVL树,旋转过程图如下:
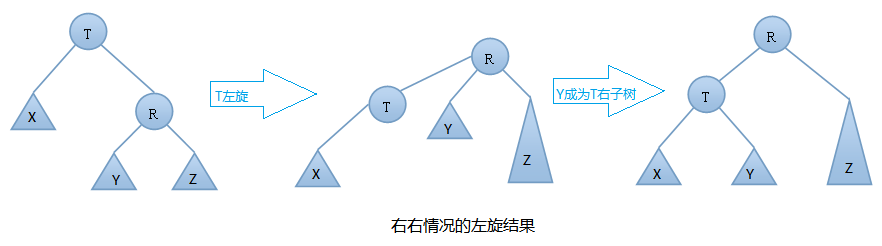
右右情况的左旋举例:
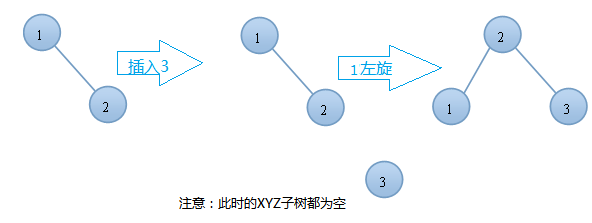
以上就是插入操作时的单旋转情况!我们要注意的是:谁是T谁是L,谁是R还有谁是X,Y,Z!T始终是开始不平衡的左右子树的根节点。显然L是T的左结点,R是T的右节点。X、Y、Y是子树当然也可以为NULL.NULL归NULL,但不能破坏插入时我上面所说的左左情况或者右右情况。
AVL树的插入,双旋转的第一种情况---左右(先左后右)旋:
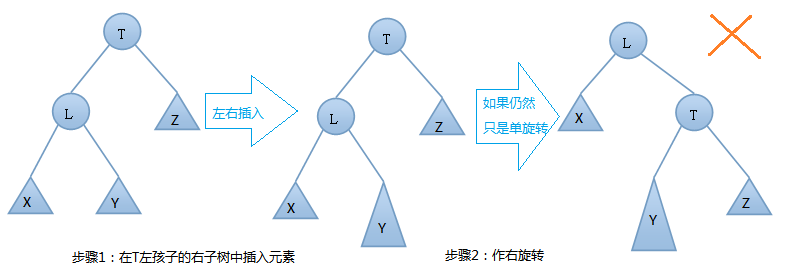
由 上图可知,我们在T结点的左结点的右子树上插入一个元素时,会使得根为T的树的左右子树高度差的绝对值不再 < 1,如果只是进行简单的右旋,得到的树仍然是不平衡的。我们应该按照如下图所示进行二次旋转:
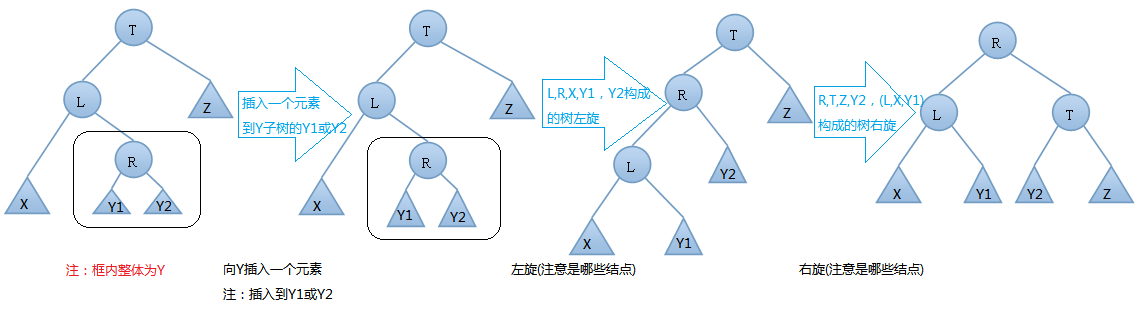
左右情况的左右旋转实例:
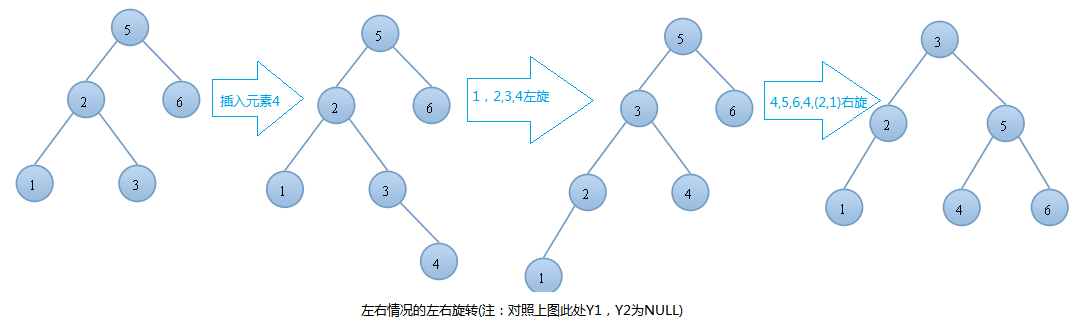
AVL树的插入,双旋转的第二种情况---右左(先右后左)旋:
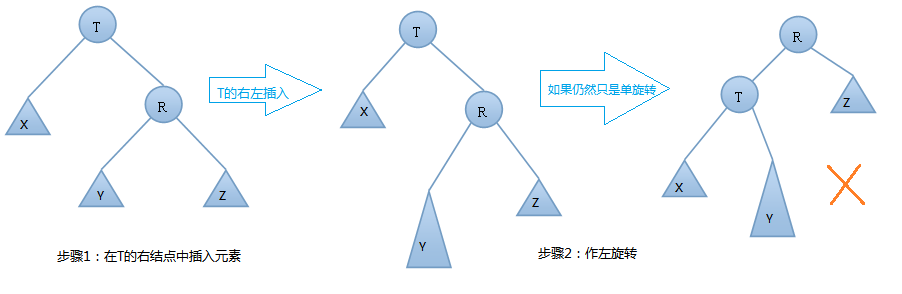
由上图可知,我们在T结点的右结点的左子树上插入一个元素时,会使得根为T的树的左右子树高度差的绝对值不再 < 1,如果只是进行简单的左旋,得到的树仍然是不平衡的。我们应该按照如下图所示进行二次旋转:
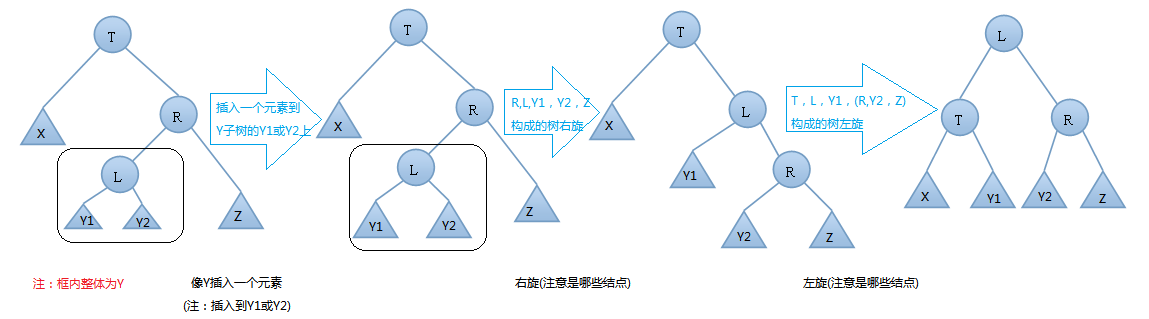
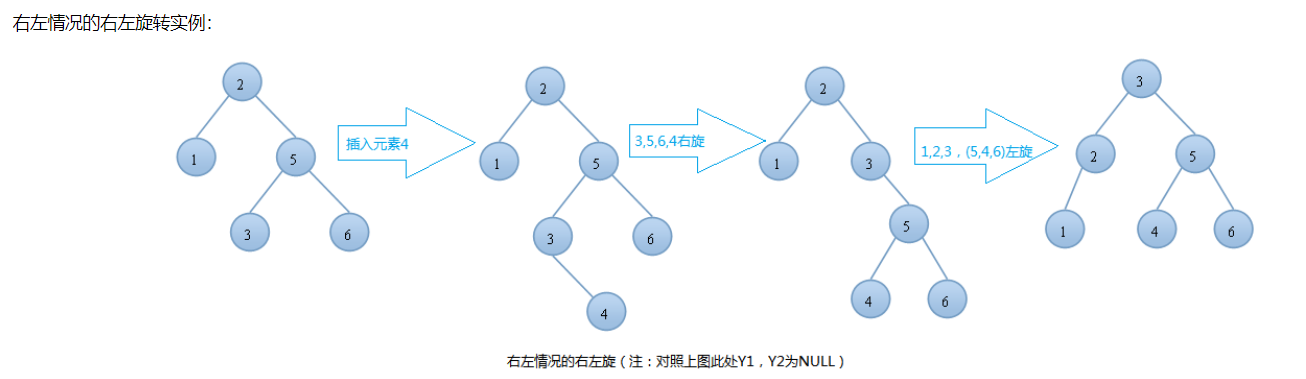
右左情况的右左旋转实例:

插入代码:
/**
* 插入结点 (测试整形插入)
*/
public AVLNode<T> insertNode(AVLNode T,T value){
if(T==null){
T = new AVLNode(value);
}else{
//走左边
if((Integer)value<(Integer)T.data){
T.lchild = insertNode(T.lchild,value);
//分情况旋转
//判断是否需要旋转
if(getHeight(T.lchild)-getHeight(T.rchild)>=2){
//左左情况
if((Integer)value<(Integer)T.lchild.data){ //这是针对插入会出现的情况判断(也可以通过比较孩子结点的当前高度来判断)
// if(getHeight(T.lchild)>getHeight(T.rchild)){
//单旋-右旋
T = singleRotateWithRight(T);
}else{
//左右情况 (排除掉相同的元素,相同元素不允许再次插入)
//先左转,再右转 LR
T = doubleRotateWithLeft(T);
}
}
//走右边
}else if((Integer)value>(Integer)T.data){
T.rchild = insertNode(T.rchild,value);
//分情况旋转
if(getHeight(T.rchild)-getHeight(T.lchild)>=2){
//右右情况
if((Integer)value>(Integer)T.rchild.data){ //这是针对插入会出现的情况判断(也可以通过比较孩子结点的当前高度来判断)
// if(getHeight(T.rchild)>getHeight(T.lchild)){
//单旋-左旋
T = singleRotateWithLeft(T);
}else{
//右左情况
T = doubleRotateWithRight(T);
}
}
}else{
//相同,不再进行插入
}
}
//每次插入都要 计算高度,这个高度是递归式的!
T.height = Max(getHeight(T.lchild),getHeight(T.rchild))+1; //每一层递归结束之前要重新计算一下高度(因为可能插入了新结点)
return T;
}
AVL树的删除操作
分析:我们用插入的例子来分析删除操作
-
首先,如果要删除的结点比当前根节点大,那么就会走左边进去
-
走左边进去删除后,判断是否需要平衡的依据一定是:
if(getHeight(T.rchild)-getHeight(T.lchild)>=2) //删掉左子树的孩子结点,肯定是右边可能会高过左边的情况 -
然后如果需要重新平衡(修复),那么要进行哪种修复呢
观察图:知道如果删除的是左边的结点,那么会出现:LL或者RL这样的旋转
RL:如果删除了左边结点的,出现了根节点2 的平衡因子从-1 变到了-2,那么再判断:根的右子树5的
左子树和右子树的高度差,当T.rchild.lchild.height >T.rchild.rchild.height,即满足上面需要RL旋转的的情况
if(getHeight(T.rchild)-getHeight(T.lchild)>=2){ //删掉左子树的孩子结点,肯定是右边可能会高过左边的情况 if(getHeight(T.rchild.lchild)>getHeight(T.rchild.rchild)){ //左子树的 右子树比左子树的左子树要高 //RL旋转 T = doubleRotateWithRight(T); //记住,因为旋转后,根节点会发生变化,一定要重新接收根结点 }else{ //RR T = singleRotateWithLeft(T); } }所有代码:
/** * 删除操作 */ public AVLNode<T> deleteNode(AVLNode T,T value){ if(T==null){ return null; }else{ //往左走 if((Integer)value<(Integer) T.data){ T.lchild = deleteNode(T.lchild,value); //函数返回新的根节点(所以要重新建立孩子与双亲间的联系) if(getHeight(T.rchild)-getHeight(T.lchild)>=2){ //删掉左子树的孩子结点,肯定是右边可能会高过左边的情况 if(getHeight(T.rchild.lchild)>getHeight(T.rchild.rchild)){ //左子树的 右子树比左子树的左子树要高 //RL旋转 T = doubleRotateWithRight(T); //记住,因为旋转后,根节点会发生变化,一定要重新接收根结点 }else{ //RR T = singleRotateWithLeft(T); } } //往右走 }else if((Integer)value>(Integer)T.data){ T.rchild = deleteNode(T.rchild,value); if(getHeight(T.lchild)-getHeight(T.rchild)>=2){ //删掉右子树的孩子结点,肯定是左边可能会高过右边的情况 if(getHeight(T.lchild.rchild)>getHeight(T.lchild.lchild)){ //LR旋转 T = doubleRotateWithLeft(T); }else{ //LL T = singleRotateWithRight(T); } } }else{ //找到了要删除的结点 //1. 没有左右孩子,删除的是叶子节点 (不用判断是否需要修复--旋转) if(T.lchild==null&&T.rchild==null){ T = null; //2. 删除的结点只有左孩子或右孩子 }else { if(T.lchild!=null){ T = T.lchild; }else if(T.rchild!=null){ T = T.rchild; }else{ //3. 删除的结点左右孩子都有 T.data = find_min_value(T.rchild); //找到最小节点,替换 T.rchild = deleteNode(T.rchild,(T)T.data); //删除替换的最小的那个结点 //判断旋转 if(getHeight(T.lchild)-getHeight(T.rchild)>=2){ if(getHeight(T.lchild.rchild)-getHeight(T.lchild.lchild)>=2){ //LR T = doubleRotateWithLeft(T); }else{ //LL T = singleRotateWithRight(T); } } } } } } if(T!=null){ //重新计算高度 T.height = Max(getHeight(T.lchild),getHeight(T.rchild))+1; } //返回新的根节点 return T; } /** * 找到最小的结点值 */ public T find_min_value(AVLNode T){ if(T.lchild==null){ return (T) T.data; }else{ return find_min_value(T.lchild); } } /** * 用于比较两棵子树高度,比较哪边高 ,用于节点高度 = Max(T.lchild.height,T.rchild.height)+1 */ public int Max(int lHeight,int rHeight){ if(lHeight>=rHeight){ return lHeight; }else{ return rHeight; } } /** * 获取结点高度,因为可能计算高度的时候,左右孩子结点很可能为空,如果不用这个方法判断的话,会导致nullPointerException */ public int getHeight(AVLNode T){ if(T==null){ return -1; }else{ return T.height; } }
测试代码
System.out.println();
System.out.println("测试AVL:");
//测试AVL
AVLTree<Integer> avlTree = new AVLTree<>();
avlTree.root = avlTree.insertNode(avlTree.root,1);
avlTree.root = avlTree.insertNode(avlTree.root,2);
avlTree.root = avlTree.insertNode(avlTree.root,3);
avlTree.root = avlTree.insertNode(avlTree.root,4);
avlTree.root = avlTree.insertNode(avlTree.root,5);
avlTree.root = avlTree.insertNode(avlTree.root,6);
avlTree.root = avlTree.insertNode(avlTree.root,7);
avlTree.root = avlTree.insertNode(avlTree.root,8);
avlTree.root = avlTree.insertNode(avlTree.root,10);
avlTree.root = avlTree.insertNode(avlTree.root,11);
avlTree.root = avlTree.insertNode(avlTree.root,12);
avlTree.root = avlTree.insertNode(avlTree.root,13);
avlTree.root = avlTree.insertNode(avlTree.root,14);
avlTree.root = avlTree.insertNode(avlTree.root,15);
avlTree.levelTraverse();
System.out.println();
System.out.println("删除5,6,7");
avlTree.deleteNode(avlTree.root,5);
avlTree.deleteNode(avlTree.root,7);
avlTree.deleteNode(avlTree.root,6);
avlTree.levelTraverse()
原来的为:
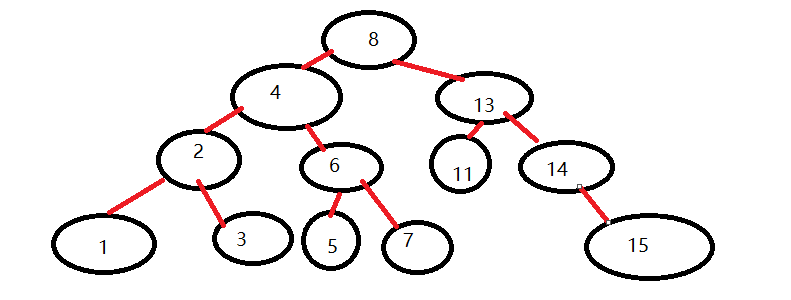
层序遍历测试结果:

通过debug查看结果:
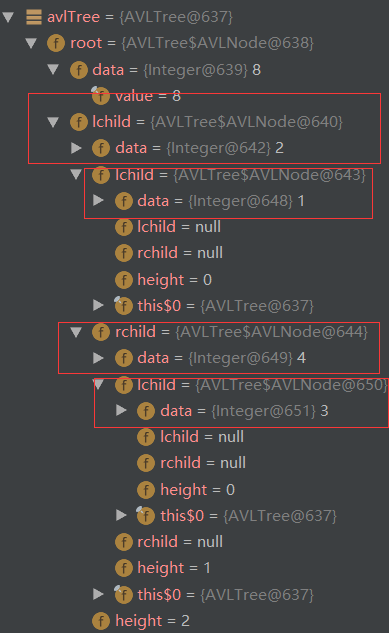
删除5,6,7后: