力扣55题、45题（跳跃游戏）

55、跳跃游戏

基本思想：

贪心算法

具体实现：

1.问题转换为跳跃覆盖范围可不可以覆盖到终点

每次移动取当前位置的最大跳跃步数，每移动一个单位，就更新最大覆盖范围

注意这里的每移动一个单位（看举例）

局部最优：每次取最大覆盖范围

整体最优：最后得到整体最大覆盖范围，看是否能到终点

2.举例

[2,3,1,0,4]

站在0这个位置，cover最初是2，也就是刚开始可以覆盖到的最大范围是2，

i每次移动只能在cover的范围内移动，也就是i可以在三个位置，0位置，1位置，2位置

i在允许范围内每个位置都会站一下，然后看他能跳到的最远距离

在0位置上往后跳，跳的是0位置允许的最大跳跃步数2，一下跳到2位置（i+nums[i]），覆盖范围还是2

在1位置上往后跳，跳的是1位置允许的最大跳跃步数3，一下跳到4位置（1+nums[1]=4），这时覆盖范围是4，已经满足条件

代码：

class Solution {
    public boolean canJump(int[] nums) {
        if (nums.length == 1) {
            return true;
        }
        //覆盖范围
        int cover = nums[0];
        //在覆盖范围内更新最大的覆盖范围
        for (int i = 0; i <= cover; i++) {
            cover = Math.max(cover, i + nums[i]);
            if (cover >= nums.length - 1) {
                return true;
            }
        }
        return false;
    }
}

45、跳跃游戏II

基本思想：

贪心算法

具体实现：

 

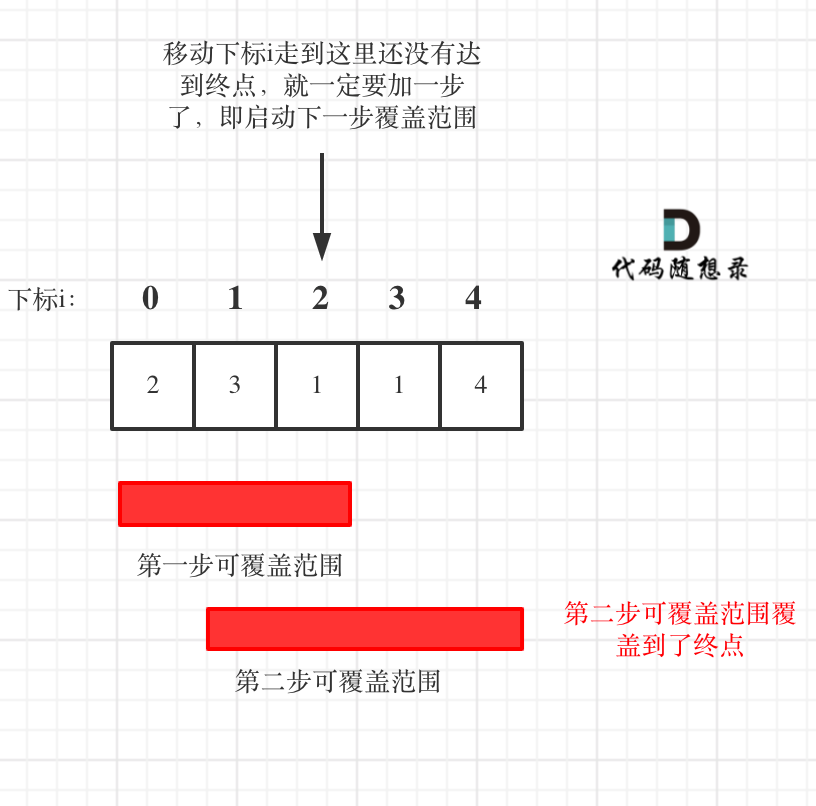
 只要是红色的区域，最多两步一定可以到。

当移动下标达到了当前覆盖的最远距离下标时，步数+1，看下一步的可以覆盖的范围，最后的步数就是最少步数。

看注释

代码：

class Solution {
    public int jump(int[] nums) {
        if (nums == null || nums.length == 0 || nums.length == 1){
            return 0;
        }
        int count = 0;//记录步数
        int curDistance = 0;//这一步的覆盖最大区域
        int maxDistance = 0;//下一步的覆盖最大区域
        for (int i = 0; i < nums.length; i++){
            //在这一步的覆盖最大区域内看下一步最远能走到哪里
            maxDistance = Math.max(maxDistance, i + nums[i]);
            //下一步最远能到的路包括了数组长度，就确定是下一步为答案，所以count++
            if (maxDistance >= nums.length - 1){
                count++;
                break;
            }
            //下一步最远不能包括数组长度的话，也要走到下一步所覆盖的区域，并继续试下下一步是否可以
            if (i == curDistance){
                curDistance = maxDistance;
                count++;
            }
        }
        return count;
    }
}