518、零钱问题II
基本思路:
钱币数量不限----完全背包问题
纯完全背包是能否凑成总金额,而本题是要求凑成总金额的方法个数
具体实现:
1、确认状态:
dp[j]:凑成总金额j的货币组合数为dp[j]
2、状态转移:
如果不使用coins[i]这个面值的硬币,就继承上面几种硬币的凑法
dp[i][j] = dp[i-1][j]
如果使用coins[i]这个面值的硬币,dp[i][j]=上面几种硬币的凑法dp[i-1][j]+新硬币加进来,剩余金额的凑法dp[i][j-coins[i-1]]
优化:dp[j] += dp[j - coins[i]];
3、初始状态:
dp[0] = 1
从dp[i]的含义上来讲就是,凑成总金额0的货币组合数为1。
4、遍历顺序:
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
for (int i = 0; i < coins.size(); i++) { // 遍历物品 for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量 dp[j] += dp[j - coins[i]]; } }
假设:coins[0] = 1,coins[1] = 5。那么就是先把1加入计算,然后再把5加入计算,得到的方法数量只有{1, 5}这种情况。而不会出现{5, 1}的情况。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
for (int j = 0; j <= amount; j++) { // 遍历背包容量 for (int i = 0; i < coins.size(); i++) { // 遍历物品 if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]]; } }
背包容量的每一个值,都是经过 1 和 5 的计算,包含了{1, 5} 和 {5, 1}两种情况。
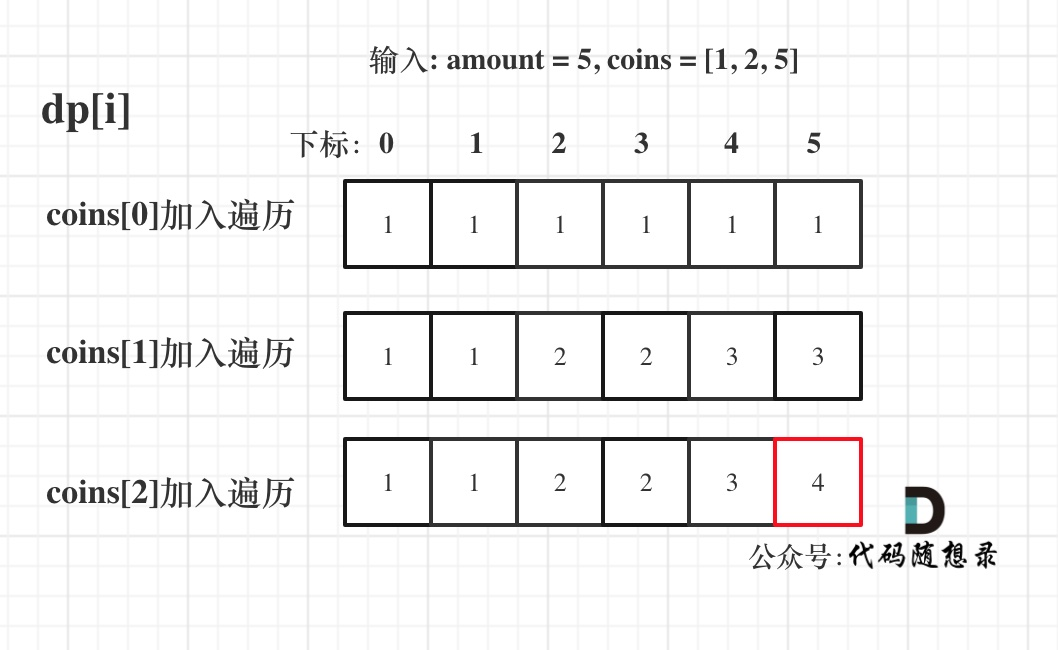
5、举例
输入: amount = 5, coins = [1, 2, 5] ,dp状态图如下:
代码:
class Solution:
def change(self, amount: int, coins: List[int]) -> int:
n = len(coins)
dp = [[0]*(amount+1) for _ in range(n+1)]
for i in range(n+1):
dp[i][0] = 1
for i in range(1,n+1):
for j in range(1,amount+1):
if j-coins[i-1]>=0:
dp[i][j] = dp[i-1][j]+dp[i][j-coins[i-1]]
else:
dp[i][j] = dp[i-1][j]
return dp[n][amount]
状态压缩
class Solution { public int change(int amount, int[] coins) { int[] dp = new int[amount + 1]; dp[0] = 1; for (int i = 0; i < coins.length; i++){ for (int j = coins[i]; j <= amount; j++){ dp[j] += dp[j - coins[i]]; } } return dp[amount]; } }
377、组合总和IV
基本思想:
数组中的数可以随便取-----完全背包
顺序不同的序列被视作不同的组合------排列
具体实现:
1、确定dp数组以及下标的含义
dp[i]是凑成目标正整数为i的排列个数
2、确定递推公式
dp[i] += dp[i - nums[j]
3、dp数组初始化
dp[0]要初始化为1,这样递推其他dp[i]的时候才会有数值基础。
dp[0] = 1 没有意义
非0下标的dp[i]初始化为0
4、确定遍历顺序
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
本题遍历顺序最终遍历顺序:target(背包)放在外循环,将nums(物品)放在内循环,内循环从前到后遍历。
5、举例

代码:
class Solution { public int combinationSum4(int[] nums, int target) { int[] dp = new int[target + 1]; dp[0] = 1; for (int i = 0; i <= target; i++){ for (int j = 0; j < nums.length; j++){ if (i >= nums[j]) { dp[i] += dp[i - nums[j]]; } } } return dp[target]; } }
70、爬楼梯进阶版
原题为每次只可以爬 1 或 2 个台阶。
改为一步一个台阶,两个台阶,三个台阶,.......,直到 m个台阶。问有多少种不同的方法可以爬到楼顶呢?
基本思想:
1阶,2阶,.... m阶就是物品,楼顶就是背包。
每一阶可以重复使用,例如跳了1阶,还可以继续跳1阶。-----完全背包
问跳到楼顶有几种方法其实就是问装满背包有几种方法。
具体实现:
1.确定dp数组以及下标的含义
dp[i]:爬到有i个台阶的楼顶,有dp[i]种方法。
2.递推公式
dp[i] += dp[i - nums[j]];
3.初始化
dp[0] = 1,其余元素都为0
4.确定遍历顺序
这是背包里求排列问题,即:1、2 步 和 2、1 步都是上三个台阶,但是这两种方法不一样
需将target(容量)放在外循环,将nums(物品)放在内循环。
每一步可以走多次,这是完全背包,内循环需要从前向后遍历。
代码:
class Solution { public int climbStairs(int n) { int[] dp = new int[n + 1]; int[] weight = {1,2}; dp[0] = 1; for (int i = 0; i <= n; i++) { for (int j = 0; j < weight.length; j++) { if (i >= weight[j]) dp[i] += dp[i - weight[j]]; } } return dp[n]; } }