目录
一、BP原理及求导
二、softmax及求导
一、BP
1、为什么沿梯度方向是上升最快方向
根据泰勒公式对f(x)在x0处展开,得到f(x) ~ f(x0) + f'(x0)(x-x0), 故得到f(x) - f(x0) ~ f'(x0)(x-x0), 所以从x0出发,变化最快,即使f(x)-f(x0)最大,也就f'(x0)(x-x0),由于f'(x0)与(x-x0)均为向量(现在x0取的是一个数,如果放在多维坐标那么x0就是一个多维向量),由余弦定理f'(x0) 与(x-x0)方向相同时,点积最大,故梯度方向是上升最快方向。
2、什么是BP
梯度反向传播(back propagation)过程就是: 由前馈神经网络得到损失函数,然后根据损失函数后向地更新每一层的权重,目的就是让损失函数变小
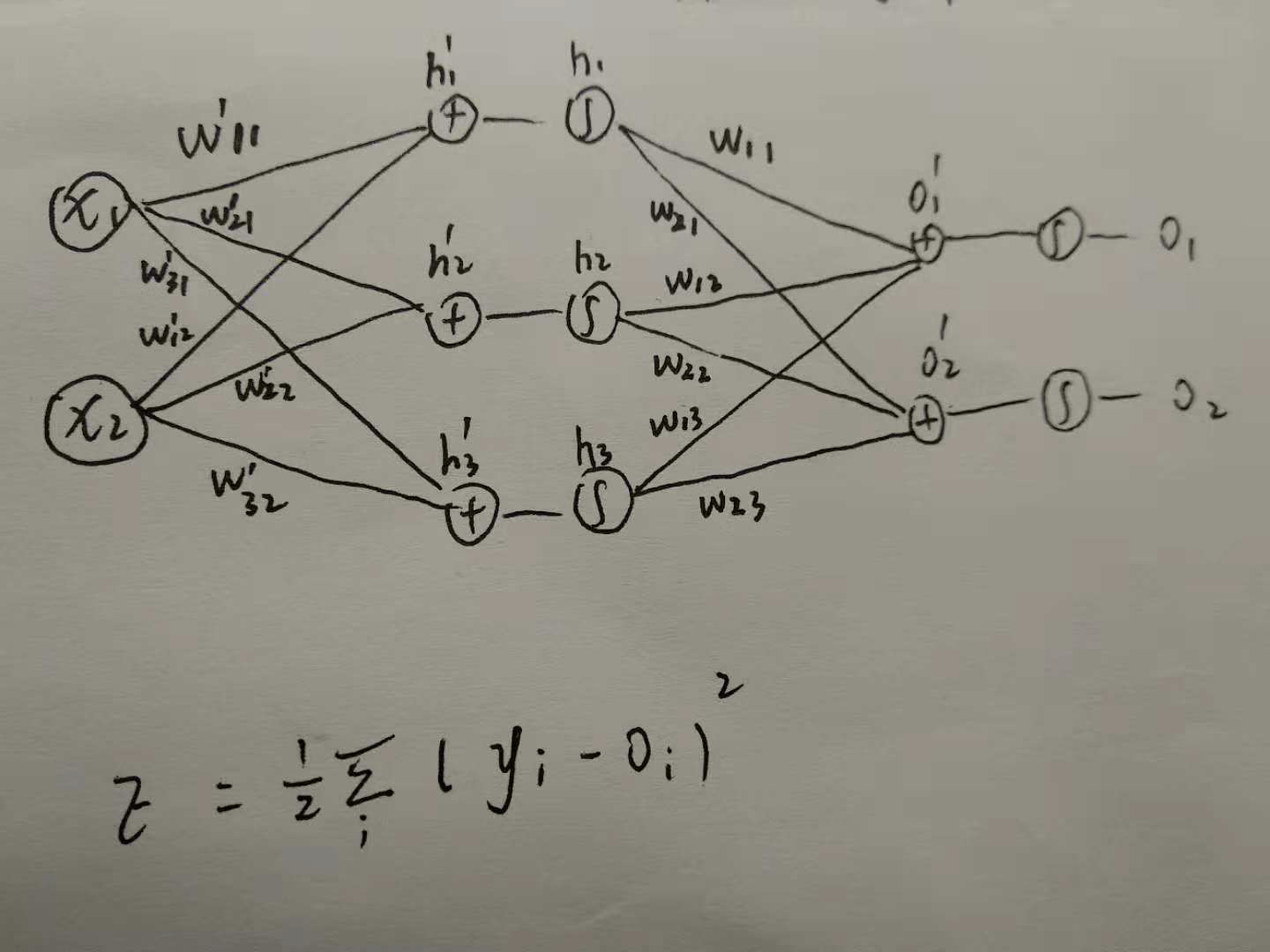


3、BP的优势
- 与从前往后进行求导相比,BP能够避开了路径被重复访问,它对于每一个路径只访问一次就能求顶点对所有下层节点的偏导值。
- 能够自适应、自主学习。这是BP算法的根本以及其优势所在,BP算法根据预设的参数更新规则,不断地调整神经网络中的参数,以达到最符合期望的输出。
4、BP的不足
- BP是基于梯度下降算法实现的,所以容易陷入局部最小而不是全局最小
- 由于BP神经网络中的参数众多,每次都需要更新数量较多的阈值和权值,故会导致收敛速度过慢
二、softmax函数及求导
1、softmax函数
在Logistic regression二分类问题中,我们可以使用sigmoid函数将输入映射到
区间中,从而得到属于某个类别的概率。将这个问题进行泛化,推广到多分类问题中,我们可以使用softmax函数,对输出的值归一化为概率值。
这里假设在进入softmax函数之前,已经有模型输出值,其中
是要预测的类别数,模型可以是全连接网络的输出
,其输出个数为
,即输出为
。
所以对每个样本,它属于类别的概率为:
通过上式可以保证 ,即属于各个类别的概率和为1。
2、求导
对softmax函数进行求导,即求
第项的输出对第
项输入的偏导。
代入softmax函数表达式,可以得到:
所以,当时:
当时:
LOSS 求导
对一个样本来说,真实类标签分布与模型预测的类标签分布可以用交叉熵来表示:
最终,对所有的样本,我们有以下loss function:
其中是样本
属于类别
的概率,
是模型对样本
预测为属于类别
的概率。
对单个样本来说,loss function对输入
的导数为:
上面对求导结果已经算出:
当时:
当时:
所以,将求导结果代入上式
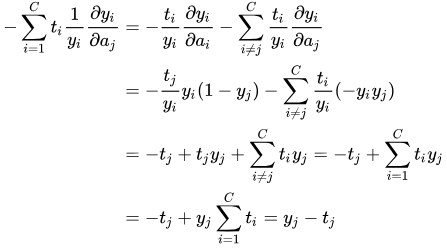
参考博客: