20172316 2018-2019-1《程序设计与数据结构》第七周学习总结
教材学习内容总结
第十一章 二叉查找树
二叉查找树:
上个星期学习了树,本星期接着学习树的一种扩展:二叉查找树(Binary Search Tree)。它最大的特点就是左孩子小于父节点,右孩子大于父节点,这种特点让二叉查找树从创建到插入元素都能维持排序的属性(主要表现在:中序遍历时元素能准确按照由小到大的顺序排列),有利于之后对树中元素的处理,特别是需要用到搜索时能大大提高搜索效率(低至O(log₂n))(不平衡树除外╰(‵□′)╯)。
| 操作 | 说明 |
|---|---|
| addElement | 往树中添加一个元素 |
| removeElement | 从树中删除一个元素 |
| removeAllOccurences | 从树中删除所指定元素的任何存在 |
| removeMin | 删除树中的最小元素 |
| removeMax | 删除树中的最大元素 |
| findMin | 返回一个指向树中最小元素的引用 |
| findMax | 返回一个指向树中最大元素的引用 |
平衡二叉查找树:
二叉查找树要表现出它高效的优点,必须要达到平衡,否则其效率甚至不如线性的链表。
(图)
为此,书中介绍了平衡化二叉查找树的方法——旋转,两种平衡化二叉查找树——AVL树、红黑树。
旋转:以右旋为例,其应用于左子树高度过高的非平衡树的平衡化中,步骤为:
- 使(子)树根的左孩子元素成为新的根元素;
- 使原根元素成为这个新树根的右孩子元素;
- 使原树根的左孩子的右孩子,成为原树根的新的左孩子。
(图)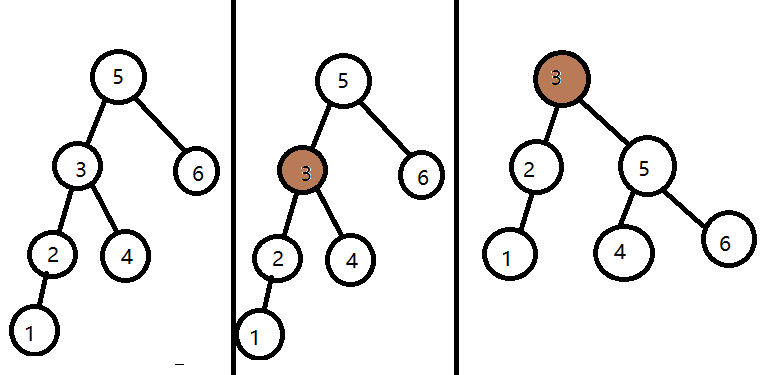
左旋反之。并非所有不平衡问题只需要一次旋转就够解决了,在具体过程中要应变地使用左右旋转。
教材学习中的问题和解决过程
一、红黑树与AVL树作为平衡化二叉查找树的手段,两者到底各有何种优越性?
- 红黑树不追求"完全平衡",书中提到:
在某种程度上,红黑树中的平衡限制没有AVL树那么严格。但是...
非严格的平衡给红黑树带来了什么好处呢?——它的旋转次数得到降低,任何不平衡将在3次旋转以内解决,对于插入和删除导致的失衡,红黑树可以更快地调整自己的平衡。
- AVL树实现完全平衡也有自己的好处,我们之所以平衡化二叉查找树,就是为了提高搜索效率,完全平衡相对应的当然就是最高效的搜索效率。
代码调试中的问题和解决过程
(无)
代码托管
(statistics.sh脚本的运行结果截图)
上周考试错题总结
上周无错题
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 6/6 | |
| 第二周 | 771/771 | 1/2 | 16/22 | |
| 第三周 | 562/1233 | 1/3 | 15/37 | |
| 第四周 | 1503/2736 | 2/5 | 15/52 | |
| 第五周 | 1152/3888 | 1/6 | 10/62 | |
| 第六周 | 787/4675 | 1/7 | 10/72 | |
| 第七周 | 1214/5889 | 1/8 | 9/81 |
结对互评
参考资料
- 《Java程序设计教程(第八版)》电子工业出版社
- 《使用码云和博客园学习简易教程》
- 《使用开源中国(码云)托管代码》
- 数据结构(一) 单链表的实现-JAVA