20172316 2018-2019-1 《程序设计与数据结构》实验二报告

课程：《程序设计与数据结构》
班级： 1723
姓名： 赵乾宸
学号：20172316
实验教师：王志强
必修/选修：必修

---

1.实验内容

1-实现二叉树

参考教材p212,完成链树LinkedBinaryTree的实现（getRight,contains,toString,preorder,postorder）
用JUnit或自己编写驱动类对自己实现的LinkedBinaryTree进行测试，提交测试代码运行截图，要全屏，包含自己的学号信息
课下把代码推送到代码托管平台

2-中序先序序列构造二叉树

基于LinkedBinaryTree，实现基于（中序，先序）序列构造唯一一棵二㕚树的功能，比如给出中序HDIBEMJNAFCKGL和后序ABDHIEJMNCFGKL,构造出附图中的树
用JUnit或自己编写驱动类对自己实现的功能进行测试，提交测试代码运行截图，要全屏，包含自己的学号信息
课下把代码推送到代码托管平台

3-决策树

自己设计并实现一颗决策树
提交测试代码运行截图，要全屏，包含自己的学号信息
课下把代码推送到代码托管平台

4-表达式树

输入中缀表达式，使用树将中缀表达式转换为后缀表达式，并输出后缀表达式和计算结果
提交测试代码运行截图，要全屏，包含自己的学号信息
课下把代码推送到代码托管平台

5-二叉查找树

完成PP11.3
提交测试代码运行截图，要全屏，包含自己的学号信息
课下把代码推送到代码托管平台

6-红黑树分析

参考http://www.cnblogs.com/rocedu/p/7483915.html对Java中的红黑树（TreeMap，HashMap）进行源码分析，并在实验报告中体现分析结果。
课下把代码推送到代码托管平台

---

2. 实验过程及结果

实验按照1-6顺序依次完成。

（1）LinkedBinaryTree的实现。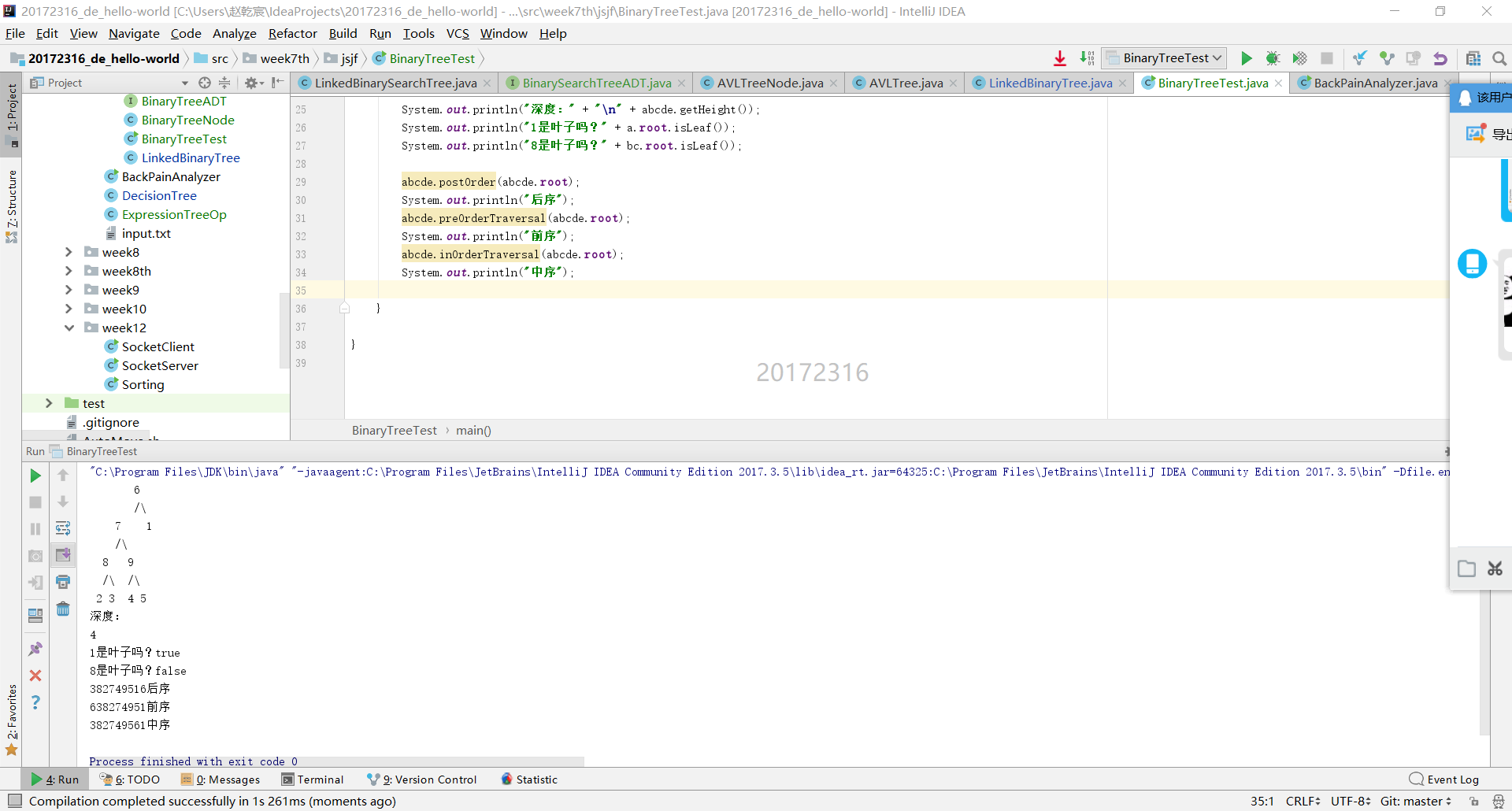

截图时未实现toString方法，后来添加了toString ，是以层序遍历的方式输出树。

（2）基于LinkedBinaryTree，实现基于（中序，先序）序列构造唯一一棵二㕚树的功能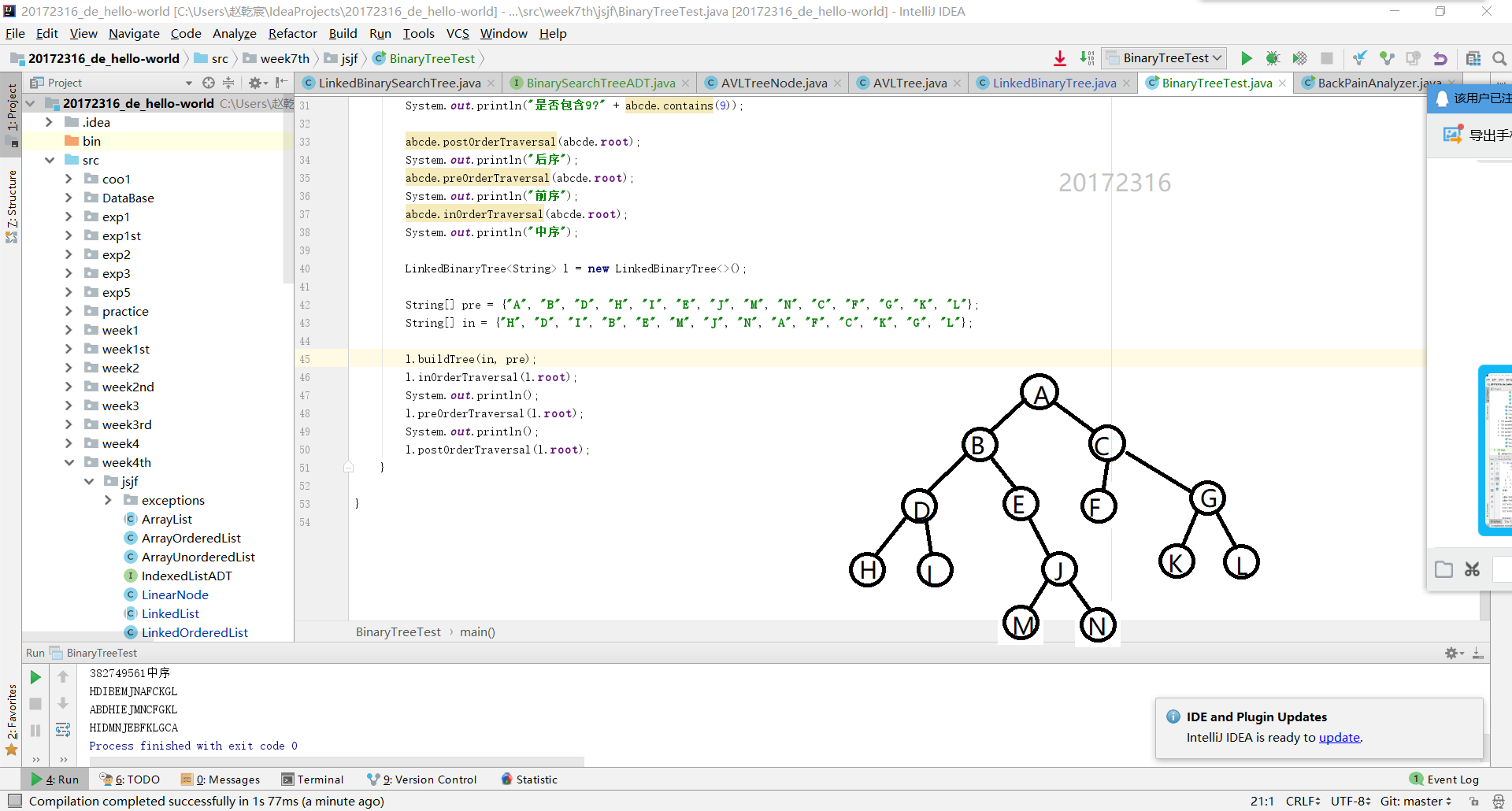

树的整体画在图上，为确定构造二叉树的正确性，输出了树的三种遍历，即最下三条，由上到下分别为先序、中序、后序

（3）自己设计并实现一颗决策树。

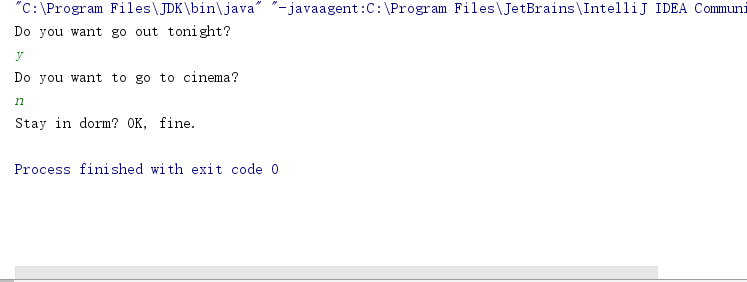
设计了一个关于“今晚去哪里学习/休息？”的决策树，由书中背部疼痛诊断器改造。

（4）输入中缀表达式，使用树将中缀表达式转换为后缀表达式，并输出后缀表达式和计算结果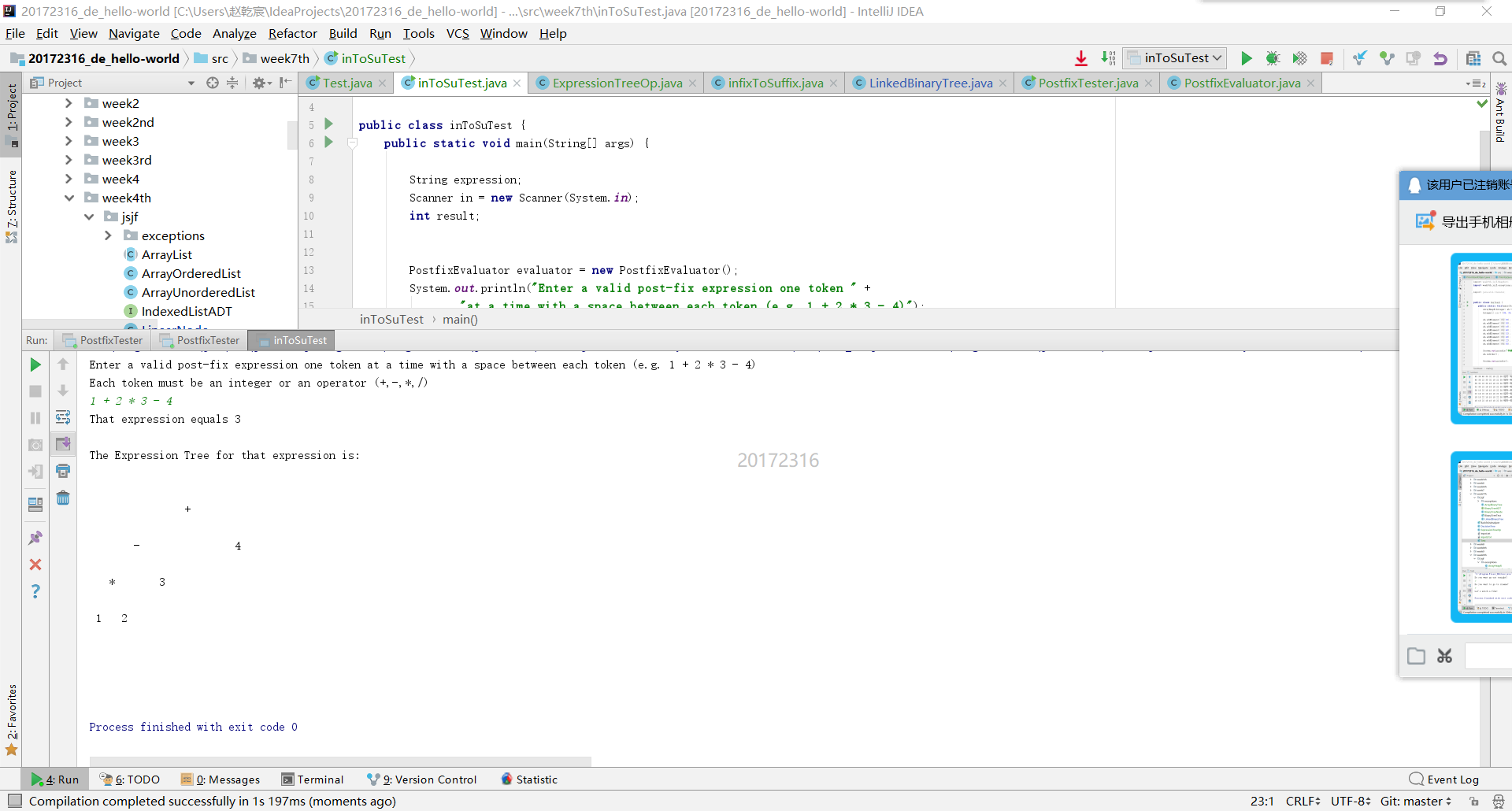

计算结果的树借用了书中例子，中缀转后缀比较复杂，也遇到了一些问题，在下方分析。

（5）完成PP11.3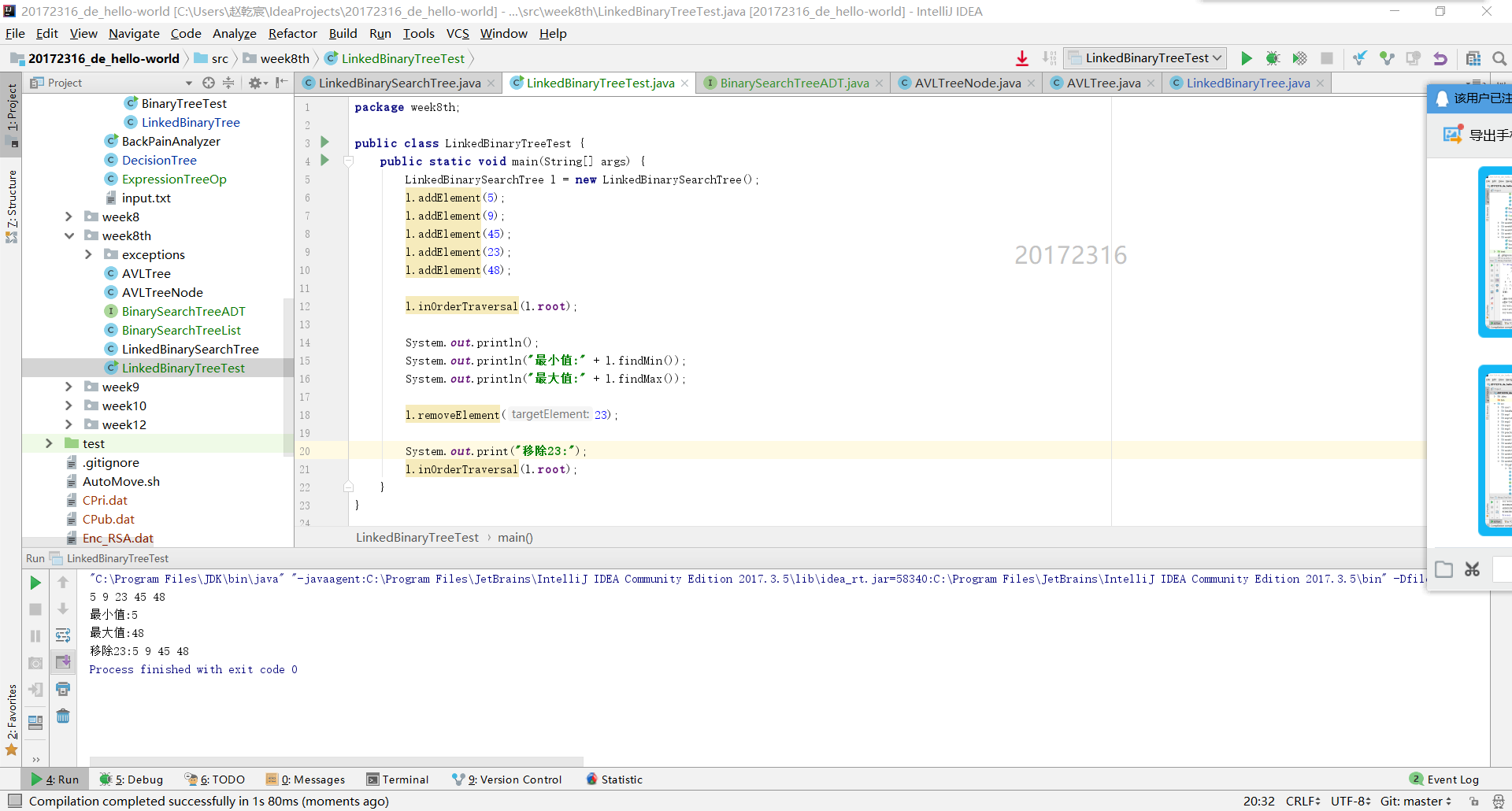

实现removeMax findMin findMax 方法，
findMin方法主要部分截取：

if (root.left == null) {
                result = root.element;
            } else {
                BinaryTreeNode<T> current = root.left;
                while (current.left != null) {
                    current = current.left;
                }
                result = current.element;
            }

实现的原理就是二叉查找树的左节点 < 父节点 < 右节点，最左的节点则是元素最小的节点，findMax同理。
removeMax则在find的基础上删除即可，由于删除的是最大节点，完全不用考虑会删除掉中间的节点导致树断开。

（6）

---

3. 实验过程中遇到的问题和解决过程

实验二-4,中缀转后缀，一开始没有思路，在网上各处查找相关文章，整理出来大致思路（↓码中注释↓），放在才最后解决

public String  toSuffix(String infix) {
        String result = "";
        String[] array = infix.split("\s+"); // 以String数组存储中缀表达式的每个数字、符号
        Stack<LinkedBinaryTree> num = new Stack(); // 数字栈
        Stack<LinkedBinaryTree> op = new Stack(); // 操作符栈

        for (int a = 0; a < array.length; a++) {
            if (array[a].equals("+") || array[a].equals("-") || array[a].equals("*") || array[a].equals("/")) {  // 判断数组中字符类型（数字or操作符），分别装入两个栈中
                if (op.empty()) {
                    op.push(new LinkedBinaryTree<>(array[a]));
                } else {
                    if ((op.peek().root.element).equals("+") || (op.peek().root.element).equals("-") && array[a].equals("*") || array[a].equals("/")) {
                        op.push(new LinkedBinaryTree(array[a]));  // 如果操作符栈中已经有“+、-”操作符而后来的的是“*、/”，压入op；若不是，进行树的构建，再压入op（优先级问题）
                    } else {
                        LinkedBinaryTree right = num.pop();
                        LinkedBinaryTree left = num.pop();
                        LinkedBinaryTree temp = new LinkedBinaryTree(op.pop().root.element, left, right);
                        num.push(temp);                                                                 // 在num中构建好子树
                        op.push(new LinkedBinaryTree(array[a]));  
                    }
                }
            } else {
                num.push(new LinkedBinaryTree<>(array[a]));
            }
        }
        while (!op.empty()) {
            LinkedBinaryTree right = num.pop();
            LinkedBinaryTree left = num.pop();
            LinkedBinaryTree temp = new LinkedBinaryTree(op.pop().root.element, left, right);
            num.push(temp);
        }

        Iterator itr = num.pop().iteratorPostOrder(); // 以后序遍历输出构建好的整棵树，后缀表达式完成。
        while (itr.hasNext()){
            result += itr.next()+" ";
        }

        return result;
    }

中缀式构建为表达式树的流程例子↓

---

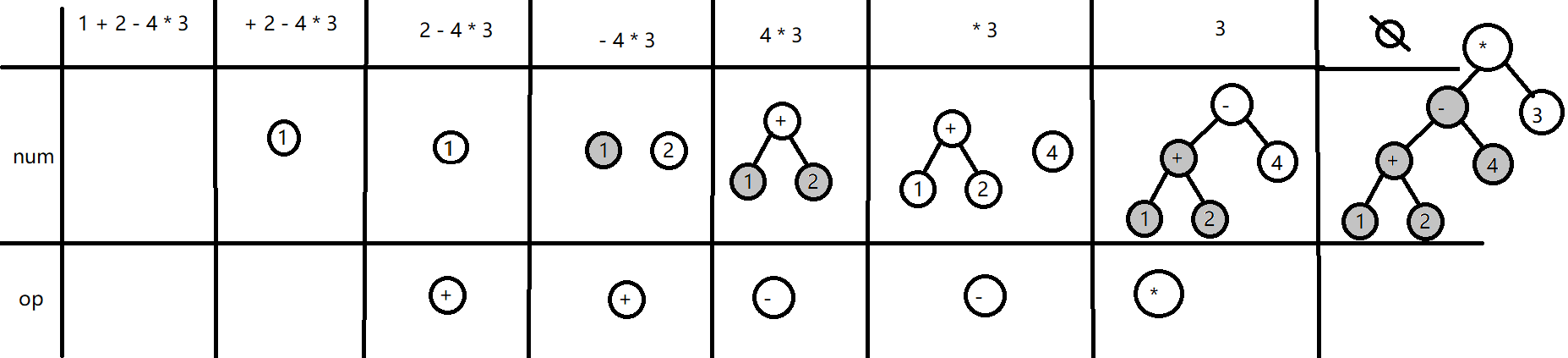
其他（感悟、思考等）

参考资料

《Java程序设计与数据结构教程（第二版）》
《Java程序设计与数据结构教程（第二版）》学习指导