哈希,英文名Hash。他就像是一个隔壁家的孩子一样,伴随着码工们的成长。听到他们的名字,我们都觉得很高大上。
在写程序的时候,一般我们都是这样被教育的:这个事情搞不定?用哈希呀!
在面试的时候,一般是这样回答的:这个算法还有优化的空间嘛?有,哈希!
在选择女朋友的时候,一般是:哈希…… 当然,被哈希的一定是码工。
好了,言归正传,聊聊算法上的哈希吧~
原来搞acm的时候,老王觉得哈希特别神秘。而且标准stl里面提供的map都不是hash,而是红黑树。后来工作以后,才更多的接触到了hash。然后发现在实际工程中,hash相关的算法用的实在太多太多。所以,最近突发奇想,才想跟大家聊聊他。
之前看一篇文章,讲哈希实际上是把一个大范围值域投影到一个小范围值域上的操作。比如:我们可以把一个字符串“老王很帅”转换成一个32位整数:Hash(string) ->int32;也可以把一个64位整数转化为32位整数:Hash(int64) -> int32;更可以把一个二进制文件转换为一个32位整数:Hash(bits) ->int32 等等。
那为什么要这样做呢?why?
老王不能完全回答这个问题,但是老王理解其中一个原因,就是将数据的多态归一化到了一个数据类型上。造成的结果就是,值域缩小,方便计算和检索。
最常见的数据结构,莫过于HashMap。我们可以将任何对象、数据存放到一个HashMap里,做到近似O(1)的插入和查找,简化了我们的实现、加速了我们的查找。
那哈希是怎么样实现的呢?how?
其实这里实际是两个问题:
1、一个key的hash值是如何计算的;
2、HashMap是如何实现存放和查找的。
那我们就来细细讲解一下上面这两个问题吧:
1、hash值的计算。
hash值的计算实际近似一个单向函数,他不要求你进行双向操作。所以,只要是你能想到的算法,基本都可以。但是,要尽量保证以下的原则:
a、可重入:同一个key,他的hash值要一样。比如:
int hash(Type key)
{
returnrand();
}
这个函数就不太符合要求,就是即使是同一个key,他得到的值也是基本不一样的。
b、尽量的分散:在key的数量够多的时候,他们求出来的hash值尽可能分散。比如:
int hash(Type key)
{
return1;
}
这个函数的效果就很差,不管key是什么,返回的值都一样。这样就导致hash以后,都集中到了一起。
只要满足以上的要求,我们就可以采用很多很多的算法,比如:md5、sha等摘要算法,也可以采用加法、乘法、位运算等等。以下是java的String类对于hash的实现:
publicint hashCode() {
int h = hash;
if (h == 0 && value.length > 0) {
char val[] = value;
for (int i = 0; i< value.length; i++) {
h = 31 * h + val[i];
}
hash = h;
}
return h;
}
这个算法就是用的加法和乘法,将字符串里面的每个字符的asc码做乘法和加法的运算。看看,是不是觉得很简单。
我们要测试可重入性其实比较简单,你需要从理论上去证明你的算法是可重入的(比如上面的算法就是,只要输入不变,输出必定不变)。
如果要测试分散性,我们就可以产生大量的随机输入值,然后统计输出的分布。如果分布比较好,说明你的哈希算法的效果就是很好的。
好了,hash值的计算就讲这么多。接下来,我们看看hash值是如何用到快速插入和查找数据的。
2、HashMap是如何存储和查找的。
最先我们就说了,hash一般是把一个大域的值映射到一个小域上,这样操作的直接后果,就是使得具有不同值的两个数据有可能得到同样一个hash值。如果我们用hash值作为存储的依据,必然会造成冲突。比如,你家住中关村大街168号,另外一个人家住上地十街10号。如果有一个hash函数将上面两个地址换算成了同一个值,然后突然之间你就和其他人共住一间屋,你肯干么?(当然,如果是一个妹子,还是值得考虑的~~ 不过……老王已经不可能了。)
所以,HashMap最大的问题,就是要解决当hash值冲突以后,我们怎么样来找到正确的key对应的数据。
在业界一般有几种算法:
a、线性探测:这是最简单的一种算法。具体操作如下:
为简单起见,我们的hash函数定义如下:
int hash(int key)
{
return key % 10;
}
为了方便讲解,我们就将数据理解为存放到一个长度为10的数组里。
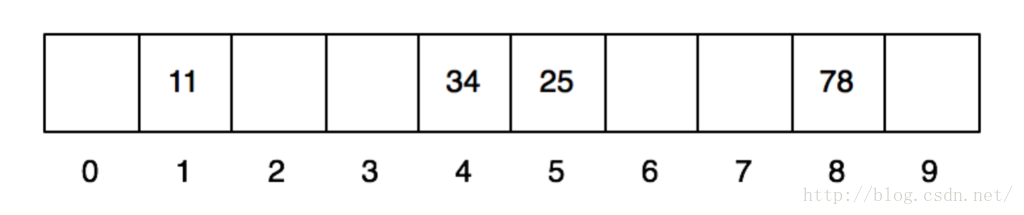
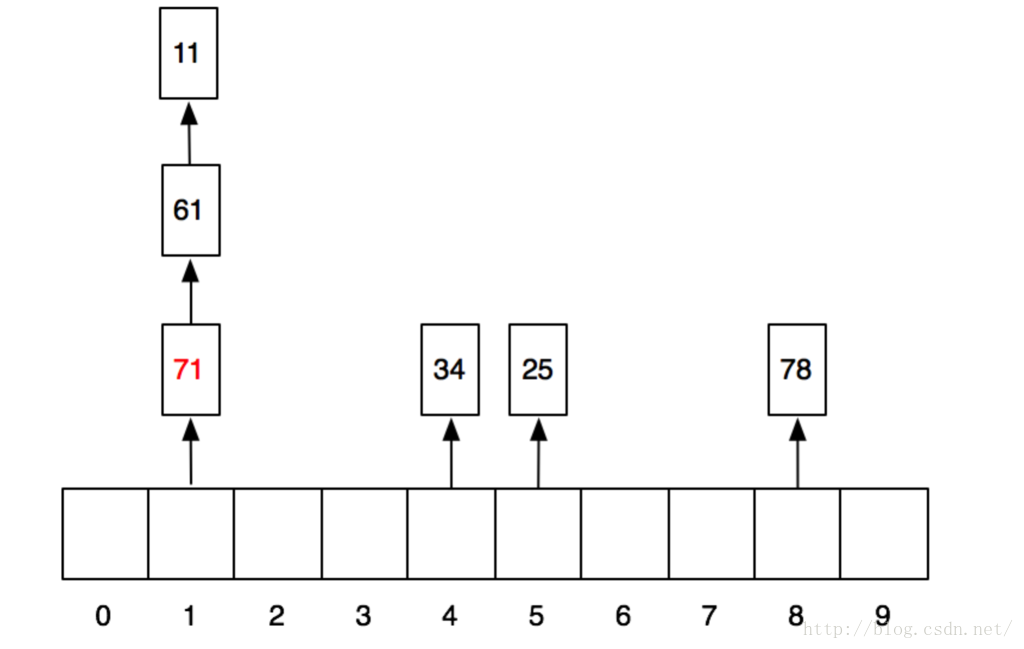
那我们依次放入11、25、34、78、61、71这几个数,看看结果会如何。我们第一步先做hash运算,分别得到上述几个数的哈希值:1、5、4、8、1、1。当放入前4个数以后,数组就变成这样了:
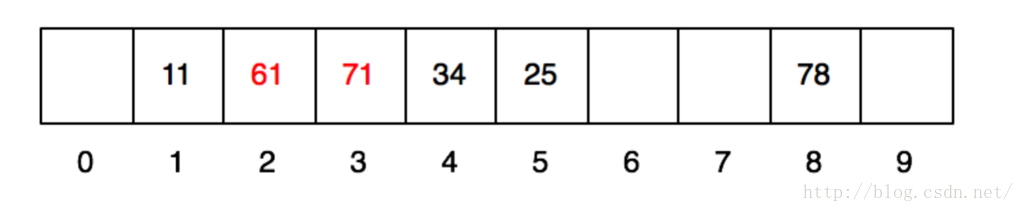
当再放入61的时候,他所需要的1号格子已经被11占领,这个时候怎么办呢?这个时候,他就顺着往后找,找到一个空的格子把自己放进去。同理,71也是。于是放完之后,格子就变成这样了:
那查找的时候,也是同样的方法,比如,我们要查找71,我们就先做hash运算,hash(71)->1。然后去1号格子找,发现住着11,不是71;接着找下一个格子,找到61,也不是;接着找,找到71,就是我们想要的。
因此,所谓线性探测,说白了,就是顺藤摸瓜,不见空格不罢休。
b、二次探测:这是稍微复杂一点的算法。其实也不难~~
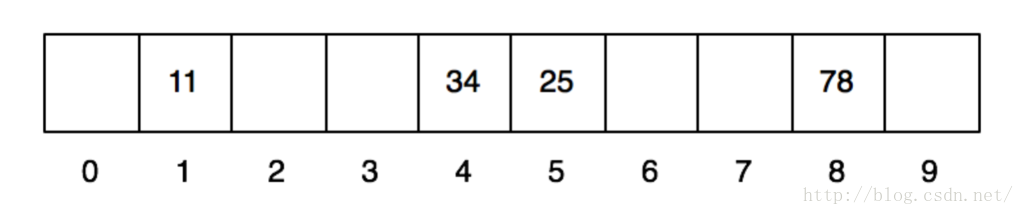
还是同样的hash值算法,我们也是10个格子。依次插入11、25、34、78、61、71这几个数。前4个插入以后,得到同样的效果:
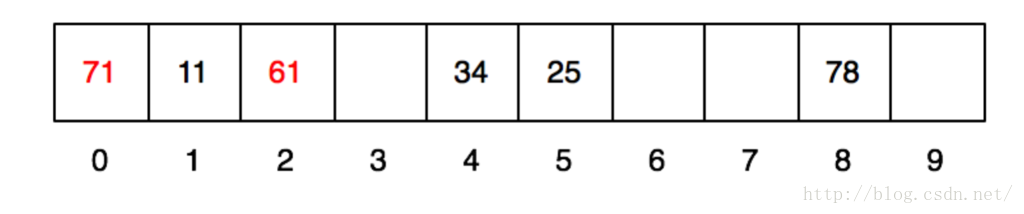
当第5个数61插入的时候,发现他要放入第一个格子中,这个时候就冲突了。怎么办呢?我们采用另外一个方式去做。就是将他的hash值,再做一次hash。每次做的时候加入一个变量,比如第一次就加入12,第二次就是22,第n次就是n2。(实际做的时候,可能会是1、-1、4、-4、9、-9……)于是,就结果就是hash(hash(61)+12) -> hash(1+12) -> 2。发现2号格子没有人存放,我们就放到2号格子。同理计算71,hash(71) -> 1,发现第一次冲突了,计算hash(hash(71) +12) -> hash(1+12) -> 2,也冲突了。那就再算:hash(hash(71) +22) ->hash(1+22) -> 5,继续冲突。再算:hash(hash(71)+32) -> hash(1+32) -> 0,终于找到0号格子住下。
查找的时候,使用同样的方法即可。
c、开链:这种方法是我们用的最多的一种方法。
线性探测和二次探测最大的问题,就是冲突后要不断的去寻找下一个位置,如果冲突了,还要不断的去寻找。直到找到这样一个空位,才能放下。如果冲突比较严重,我们插入和查找的时间都会比较长,甚至有可能出现O(n)的算法复杂度。这样就失去了hash的作用。
那开链提供了另外一种方式。就是冲突的时候,我不是去格子里寻找一个位置,而是在格子里挂载一个链式的结构,然后不断的往这个链式结构中放入hash值相同的元素。
我们具体来看看怎么操作的吧。
当我们再加入61的时候,他就应该放到第一个格子的链表中。如下图:
为啥要放到链的第一个,而不是最后一个呢?很简单,这样实现的时间复杂度是O(1),否则还要遍历这个链。
同理,我们把71也放入到这个链中:
好了。插入就是这样。剩下的查找就很简单了。我们先求出hash值,然后到对应的格子里去找到链表,遍历链表就可以了。
很多基础库也是这样实现的代码。不过我们仔细分析就会发现,如果某个hash值的链特别长的话,其实在链里查找元素一样是非常慢的。那还有没有方法改进呢?
答案是有的!(老王这样问,肯定是有解法的嘛~)
java1.8的HashMap,在实现的时候,就对这种做了优化。当链表长度大于等于8的时候,就将链表转化为了红黑树。那在这个红黑树里查找的速度,立马就从O(n)变成O(lgn)的复杂度。如果红黑树的结点个数少于等于6个,又重新变会链表。所以,老王看了java的这个实现,还是很佩服写JDK的码工们~