z-score 的基础概念
这种方法基于原始数据的均值(mean)和标准差(standard deviation)进行数据的标准化。
将A的原始值x使用z-score标准化到x’,
x′=x−μδ ,μ为数据的均值, δ为方差。
z-score标准化方法适用于属性A的最大值和最小值未知的情况,或有超出取值范围的离群数据的情况。
将数据按其属性(按列进行)减去其均值,然后除以其方差。
最后得到的结果是,对每个属性/每列来说所有数据都聚集在0附近,方差值为1。
Python使用平滑移动+z-score进行时序数据的异常值检测 (调参总结见代码注释及后续结果输出)
# -*- coding: utf-8 -*-
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import math
def smoothed_z_score_test(data):
""" 一点调参总结
平滑z-score 测试
:param y: 原DataFrame的数据列
:param lag: 滞后数(初始滑动窗口大小) , 建议设置为业务线的循环周期需要的天数, 看业务线的周期规律——估算出回归周期,乘上系数; 按天变化的设置为7*4天, 按周的设置为7*4*4天, 等
:param threshold: 阈值 = 当前值超出前面所有的值的平均水平的绝对值 除以 前面所有的值的标准差的倍数 的上限, 建议2倍
:param influence: 平滑系数,发生异常点时使用的平滑系数,(0,1),值越大越受当前值的影响,及异常值的折算系数,建议0.5左右
:return:
"""
input_id = 157 # 输入数据的id
output_id = 161 # 聚合并输出的数据的id
start_date = '2017-01-01' # 开始转换的时间
end_date = '2020-01-31' # 结束转换的时间
y = data[input_id]['data_value']
# 设置z-score参数
lag, threshold, influence = 8 * 2, 2, 0.5
signals = np.zeros(len(y))
filteredY = np.array(y)
avgFilter = [0] * len(y)
stdFilter = [0] * len(y)
avgFilter[lag - 1] = np.mean(y[0:lag])
stdFilter[lag - 1] = np.std(y[0:lag])
for i in range(lag, len(y)):
if abs(y[i] - avgFilter[i - 1]) > threshold * stdFilter[i - 1]:
if y[i] > avgFilter[i - 1]:
signals[i] = 1
else:
signals[i] = -1
filteredY[i] = influence * y[i] + (1 - influence) * filteredY[i - 1]
avgFilter[i] = np.mean(filteredY[(i - lag + 1):i + 1])
stdFilter[i] = np.std(filteredY[(i - lag + 1):i + 1])
else:
signals[i] = 0
filteredY[i] = y[i]
avgFilter[i] = np.mean(filteredY[(i - lag + 1):i + 1])
stdFilter[i] = np.std(filteredY[(i - lag + 1):i + 1])
series_dict = dict(signals=np.asarray(signals),
avgFilter=np.asarray(avgFilter),
stdFilter=np.asarray(stdFilter)
)
data[output_id] = data[input_id].copy()
data[output_id]['data_value'] = np.asarray(series_dict['signals'])
def paint(dfs=[], labels=[], title='暂无'):
assert len(dfs) == len(labels)
plt.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文标签
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(16, 8))
for i in range(0, len(dfs)):
plt.plot(dfs[i]['data_value'], label=labels[i])
plt.legend(loc='best')
plt.title(title)
plt.show()
if __name__ == '__main__':
idx = pd.date_range('2020-01-01', periods=90, freq='D')
cos_arr = np.arange(len(idx)) * np.pi / 8
for i in range(0, len(cos_arr)):
cos_arr[i] = math.cos(cos_arr[i])
# 人为制造两个异常点
cos_arr[24] -= 1
cos_arr[25] -= 2
cos_arr[32] += 1
data_value = pd.Series(cos_arr, index=idx)
# 设置z-score参数
df = pd.DataFrame({
'data_time': idx, # 时间列
'data_value': data_value # 数据列
})
data = {}
data[157] = df
data[161] = pd.DataFrame()
smoothed_z_score_test(data)
paint(dfs=[data[157], data[161]], labels=['origin', 'signal'])
输出绘图
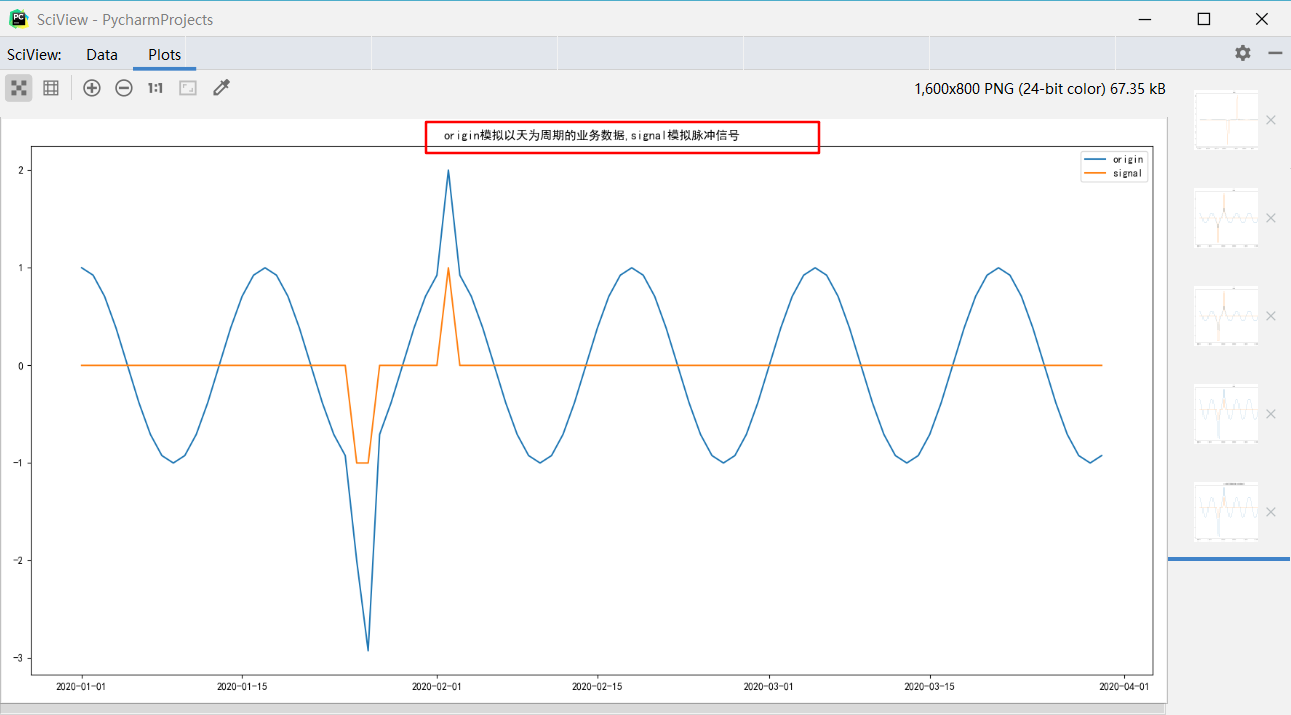
正弦函数模拟测试01 (上面的代码的直接输出)
- 输入数据特征: 回归周期为8*2天,阈值2倍, 异常值折算为0.5倍
- 对应使用的参数为lag, threshold, influence = 8 * 2, 2, 0.5
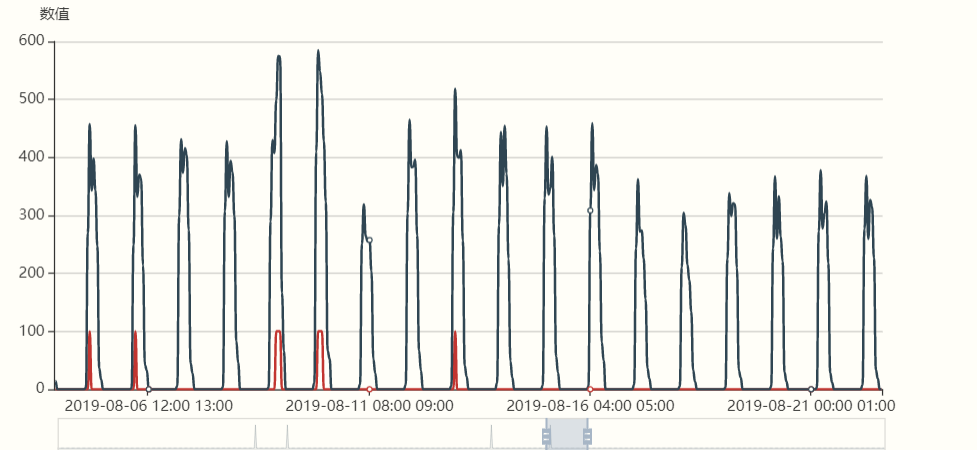
历史某业务线数据测试 (多次调整后)
- 输入数据特征: 回归周期为24小时(再74后就是一个月),阈值3倍, 异常值折算为0.5倍
- 使用参数为: lag, threshold, influence = 2474, 3, 0.5
- 蓝线为业务数据, 红线为 z-score计算出的脉冲数据乘以100倍
参考链接:
https://www.imooc.com/article/39419 python 数据标准化常用方法,z-scoremin-max标准化
https://zhuanlan.zhihu.com/p/39453139 Smoothed z-score algorithm简介配图
https://stackoverflow.com/questions/22583391/peak-signal-detection-in-realtime-timeseries-data/43512887#43512887 源代码、Smoothed z-score algorithm实践代码