cf486C Palindrome Transformation

C. Palindrome Transformation

time limit per test 1 second

memory limit per test 256 megabytes

input standard input

output standard output

Nam is playing with a string on his computer. The string consists of n lowercase English letters. It is meaningless, so Nam decided to make the string more beautiful, that is to make it be a palindrome by using 4 arrow keys: left, right, up, down.

There is a cursor pointing at some symbol of the string. Suppose that cursor is at position i (1 ≤ i ≤ n, the string uses 1-based indexing) now. Left and right arrow keys are used to move cursor around the string. The string is cyclic, that means that when Nam presses left arrow key, the cursor will move to position i - 1 if i > 1 or to the end of the string (i. e. position n) otherwise. The same holds when he presses the right arrow key (if i = n, the cursor appears at the beginning of the string).

When Nam presses up arrow key, the letter which the text cursor is pointing to will change to the next letter in English alphabet (assuming that alphabet is also cyclic, i. e. after 'z' follows 'a'). The same holds when he presses the down arrow key.

Initially, the text cursor is at position p.

Because Nam has a lot homework to do, he wants to complete this as fast as possible. Can you help him by calculating the minimum number of arrow keys presses to make the string to be a palindrome?

Input

The first line contains two space-separated integers n (1 ≤ n ≤ 105) and p (1 ≤ p ≤ n), the length of Nam's string and the initial position of the text cursor.

The next line contains n lowercase characters of Nam's string.

Output

Print the minimum number of presses needed to change string into a palindrome.

Sample test(s)

input

8 3
aeabcaez

output

6

Note

A string is a palindrome if it reads the same forward or reversed.

In the sample test, initial Nam's string is: 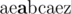 (cursor position is shown bold).

In optimal solution, Nam may do 6 following steps:

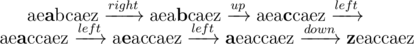
The result, 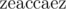, is now a palindrome.

题意是给一个长为n的串、一个初始位置，每次可以左移一格、右移一格、把当前这一格位置上的字母upcase、downcase，求把它变成回文串的最小步数

注意到回文串是对称的，所以你在i位置修改和在n-i+1位置修改是一样的，代价不变

所以只要考虑位置移动的代价就好了

显然只修改前半边的字母或者只修改后半边的字母是最优的

然后只要考虑一下从m出发先去l再去r优还是先去r再去l优，自己推一推就好了

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<queue>
#include<deque>
#include<set>
#include<map>
#include<ctime>
#define LL long long
#define inf 0x7ffffff
#define pa pair<int,int>
#define pi 3.1415926535897932384626433832795028841971
using namespace std;
int cost[1000010];
char c[1000010];
int n,m,l=inf,r=0,tot=0;
inline LL read()
{
    LL x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
void ex()
{
	printf("NO");
	exit(0);
}
int main()
{
	n=read();m=read();
	if (m>n/2)m=n-m+1;
	for (int i=1;i<=n;i++)
	{
		char ch=getchar();
		while (ch<'a'||ch>'z')ch=getchar();
		c[i]=ch;
	}
	for (int i=1;i<=n/2;i++)
	{
		cost[i]=min(abs(c[i]-c[n-i+1]),abs(c[i]+26-c[n-i+1]));
		cost[i]=min(cost[i],abs(c[i]-26-c[n-i+1]));
		tot+=cost[i];
	}
	for (int i=1;i<=n/2;i++)
	{
		if (cost[i])
		{
			l=min(l,i);
			r=max(r,i);
		}
	}
	if (tot==0)printf("0");
	else
	printf("%d
",tot+r-l+min(abs(m-r),abs(m-l)));
}