原文:http://www.cnblogs.com/graphics/archive/2009/11/28/1612832.html
如果您正在学习ArcBall技术或者您对于屏幕坐标到三维坐标的转换有些模糊,那么一定不要错过本篇。ScreenToVector函数是微软DXUT框架中AcrBall类中的一个函数,它的作用是完成二维屏幕坐标到三维球坐标的转换,先看一下函数定义
 代码
代码
2 {
3 // Scale to screen
4 FLOAT x = -( fScreenPtX - m_Offset.x - m_nWidth / 2 ) / ( m_fRadius * m_nWidth / 2 );
5 FLOAT y = ( fScreenPtY - m_Offset.y - m_nHeight / 2 ) / ( m_fRadius * m_nHeight / 2 );
6
7 FLOAT z = 0.0f;
8 FLOAT mag = x * x + y * y;
9
10 if( mag > 1.0f )
11 {
12 FLOAT scale = 1.0f / sqrtf( mag );
13 x *= scale;
14 y *= scale;
15 }
16 else
17 z = sqrtf( 1.0f - mag );
18
19 // Return vector
20 return D3DXVECTOR3( x, y, z );
21 }
函数的输入是屏幕坐标,输出是一个三维向量-这个向量位于ArcBall的球面上。为什么要分析这个函数?首先是它很重要,其次它比较难以理解,它的第一行代码让很多刚刚接触它的人都搞不明白,为什么要将x的值取反呢?我苦苦思索了很久,又苦苦搜索了很久,但是始终找不到满意的答案,于是就自己硬着头皮分析。经过好几周的苦战,终于有点眉目了,下面我就把自己的一点看法分享给大家。我不敢保证我的分析是正确的,只希望能给您一点启发,如果您发现了什么错误,或者您有更简单的方法,请一定告诉我,先谢过!
为了更好地便于大家理解,首先要强调几个知识点
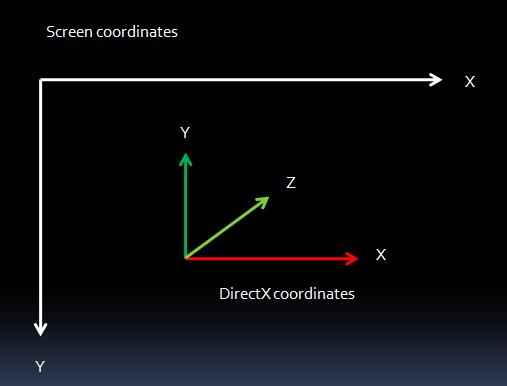
1. Windows屏幕/窗口坐标特点:以窗口左上角为原点,X值向右递增,Y值向下递增
2. DirectX使用的是左手系:X轴指向右,Y轴指向上,Z轴垂直屏幕指向内侧
3. Quaternion表示的旋转满足右手系-绕旋转轴逆时针旋转(对着旋转轴向原点看)
好了,上一张图,对比一下屏幕坐标与DirectX坐标的差异
下面开始分析代码,先看头两行代码,他们的作用是将屏幕坐标转换为[0-1]范围内的值,通常窗口的偏移量设置为0,而ArcBall的半径设置为1,所以这两行代码可以转化为下面的形式
 代码
代码
2 FLOAT y = ( fScreenPtY - m_nHeight / 2 ) / ( m_nHeight / 2 );
3
接下来的代码求z的值,如果x,y构成的二维向量的模>1,那么直接令z=0,否则的话计算z值,并使三维向量的模保持为1,这是为了方便后面求旋转角度和旋转轴的计算
为什么X的值取反?
首先:由z的计算过程知,z的值永远>=0,又因为DirectX使用左手系,所以,实际上这里是用的是屏幕内侧的半球来进行旋转的!这就要求ArcBall的旋转方向与鼠的标滑动方向相反,进而要求屏幕坐标的x,y值与ArcBall的x,y值相反,因为屏幕坐标无z值一说,所以z值不用考虑。
因为屏幕坐标的x轴和DirectX坐标系的x轴方向一致,所以将x值取反,而对于y轴来说,本来就是相反的,所以不用处理了。这里实际上包含了下面这个过程
注:这个图中的球是屏幕内部的半球,由于画的不好,效果不是很明显。
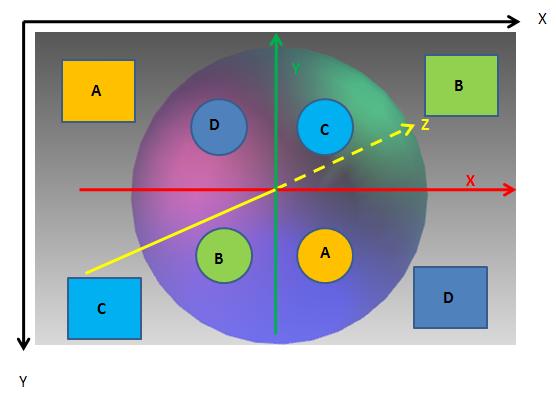
由上面的图可知,将x值取反后,实际上是将屏幕的左上区域映射到ArcBall的右下半球,右上区域映射到左下半球,左下区域映射到右上半球,右下区域映射到左上半球,哈哈,绕迷糊了吧,不过对着图还是比较好理解的,映射的方向由同种颜色的矩形到圆形表示。
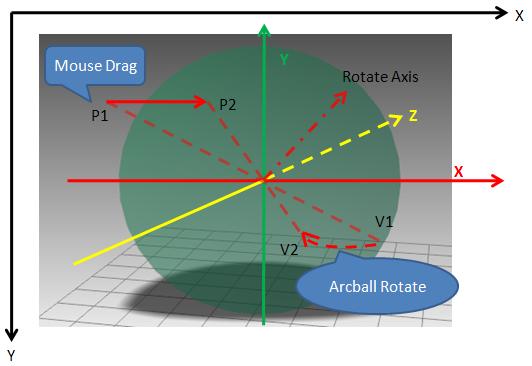
那么我们看看旋转是如何实现的,再看图
这个图表示,当用户在窗口左上区域向右拖动鼠标,起点和终点分别是P1和P2,那么将在ArcBall的右下区域产生两个向量,分别是V1和V2,而ArcBall旋转的方向则是从V1到V2,旋转轴是由V1和V2的叉积确定的。
有些时候为了追求简单,往往会将问题搞得更复杂,就像这个函数一样,可能是写这个函数的哥们为了简便将x的值取反,使我们理解起来如此困难,如果他能多写一个负号的话,那么问题就简单多了,为什么这么说呢?
因为使用屏幕内测的半球导致鼠标拖拽方向和ArcBall的旋转方向相反,如果我们使用屏幕外侧的半球不就简单了嘛!Yeah!you got it!
将x值保持不变,y,z的值都取反,代码变成下面这样
 代码
代码
2 FLOAT x = ( fScreenPtX - m_Offset.x - m_nWidth / 2 ) / ( m_fRadius * m_nWidth / 2 );
3 FLOAT y = -( fScreenPtY - m_Offset.y - m_nHeight / 2 ) / ( m_fRadius * m_nHeight / 2 );
4
5 FLOAT z = 0.0f;
6 FLOAT mag = x * x + y * y;
7
8 if( mag > 1.0f )
9 {
10 FLOAT scale = 1.0f / sqrtf( mag );
11 x *= scale;
12 y *= scale;
13 }
14 else
15 z = -sqrtf( 1.0f - mag );
16
这样窗口坐标的x,y轴就与DirectX坐标系的x,y轴重合了。而z值永远<=0保证了使用的是外侧的半球,这样鼠标的拖拽方向就和ArcBall的旋转方向一致了!上面的分析都是针对DirectX进行的,如果您使用的是OpenGL, 则情况恰好相反,OpenGL使用的是右手系,所以直接将y值取反就可以了。你明白了么?
Happy Coding!!!
== THE END ==