python学习笔记：线性回归

线性回归

1.一般形式

w叫做x的系数，b叫做偏置项。

2 如何计算

2.1 Loss Function--MSE（均方误差）

利用梯度下降法找到最小值点，也就是最小误差，最后把 w 和 b 给求出来。

3 过拟合、欠拟合如何解决

使用正则化项，也就是给loss function加上一个参数项，正则化项有L1正则化、L2正则化、ElasticNet

详细了解，可参考视频什么是 L1 L2 正规化

3.1 L1正则（lasso回归）

表示上面的 loss function ，在loss function的基础上加入w参数的绝对值惩罚项。

求解J0的过程可以画出等值线。同时L1正则化的函数也可以在w1w2的二维平面上画出来。如下图：

3.2 L2正则化(岭回归)

方程：

求解J0的过程可以画出等值线。同时L2正则化的函数L也可以在w1w2的二维平面上画出来

L1正则化(Lasso回归)可以使得一些特征的系数变小,甚至还使一些绝对值较小的系数直接变为0，从而增强模型的泛化能力 。对于高的特征数据,尤其是线性关系是稀疏的，就采用L1正则化(Lasso回归),或者是要在一堆特征里面找出主要的特征，那么L1正则化(Lasso回归)更是首选了。

3.3 ElasticNet（弹性网络回归）

ElasticNet综合了L1正则化项和L2正则化项，以下是它的公式：

$min(frac{1}{2m}[sum_{i=1}^{m}({y_i}{'}-y_i)^{2+lambdasum_{j=1}}{n} heta_j^{2]+lambdasum_{j=1}}{n}| heta|)$

ElasticNet在我们发现用Lasso回归太过(太多特征被稀疏为0),而岭回归也正则化的不够(回归系数衰减太慢)的时候，可以考虑使用ElasticNet回归来综合，得到比较好的结果。

4 几种回归模型的优缺点

机器学习中的五种回归模型及其优缺点

5 如何选择各种回归模型

你应该掌握的 7 种回归模型

6 线性回归-简单实现房屋价格预测

• 数据说明：
  数据主要包括2014年5月至2015年5月美国King County的房屋销售价格以及房屋的基本信息。
  数据分为训练数据和测试数据，分别保存在kc_train.csv和kc_test.csv两个文件中。
  其中训练数据主要包括10000条记录，14个字段，主要字段说明如下：
  第一列“销售日期”：2014年5月到2015年5月房屋出售时的日期
  第二列“销售价格”：房屋交易价格，单位为美元，是目标预测值
  第三列“卧室数”：房屋中的卧室数目
  第四列“浴室数”：房屋中的浴室数目
  第五列“房屋面积”：房屋里的生活面积
  第六列“停车面积”：停车坪的面积
  第七列“楼层数”：房屋的楼层数
  第八列“房屋评分”：King County房屋评分系统对房屋的总体评分
  第九列“建筑面积”：除了地下室之外的房屋建筑面积
  第十列“地下室面积”：地下室的面积
  第十一列“建筑年份”：房屋建成的年份
  第十二列“修复年份”：房屋上次修复的年份
  第十三列"纬度"：房屋所在纬度
  第十四列“经度”：房屋所在经度

• 数据下载：点击下载，密码：mfqy。

• 说明：只是测试跑通整个流程，未做指标筛选

# 导入相关python库
import os
import numpy as np
import pandas as pd

# 设定随机种子数，目的是每次随机选择出来的数据都是一样de
np.random.seed(35)

#使用matplotlib库画图
import matplotlib
import seaborn
import matplotlib.pyplot as plot

from sklearn import datasets

# 读取数据
train = pd.read_csv('kc_train.csv')
test = pd.read_csv('kc_test.csv')
train.head(5)

	20150302	545000	3	2.25	1670	6240	1	8	1240	430	1974	0	47.6413	-122.113
0	20150211	785000	4	2.50	3300	10514	2.0	10	3300	0	1984	0	47.6323	-122.036
1	20150107	765000	3	3.25	3190	5283	2.0	9	3190	0	2007	0	47.5534	-122.002
2	20141103	720000	5	2.50	2900	9525	2.0	9	2900	0	1989	0	47.5442	-122.138
3	20140603	449500	5	2.75	2040	7488	1.0	7	1200	840	1969	0	47.7289	-122.172
4	20150506	248500	2	1.00	780	10064	1.0	7	780	0	1958	0	47.4913	-122.318

# 查看是否有缺失值
# train.info()

# 由于第二列是需要预测的价格，我们新建一个dataframe先分离出来，为y
target = train.iloc[:,1]
target.head()

0    785000
1    765000
2    720000
3    449500
4    248500
Name: 545000, dtype: int64

# 剩下的字段组成x
train_x = train.drop(['545000','20150302'],axis=1)
train_x.head()

	3	2.25	1670	6240	1	8	1240	430	1974	0	47.6413	-122.113
0	4	2.50	3300	10514	2.0	10	3300	0	1984	0	47.6323	-122.036
1	3	3.25	3190	5283	2.0	9	3190	0	2007	0	47.5534	-122.002
2	5	2.50	2900	9525	2.0	9	2900	0	1989	0	47.5442	-122.138
3	5	2.75	2040	7488	1.0	7	1200	840	1969	0	47.7289	-122.172
4	2	1.00	780	10064	1.0	7	780	0	1958	0	47.4913	-122.318

# 特征缩放
from sklearn.preprocessing import MinMaxScaler

minmaxscaler = MinMaxScaler()
minmaxscaler.fit(train_x)
scaler_train_x = minmaxscaler.transform(train_x)
scaler_train_x = pd.DataFrame(scaler_train_x, columns=train_x.columns)
scaler_train_x.head()

/Users/zxx/anaconda3/lib/python3.7/site-packages/sklearn/preprocessing/data.py:334: DataConversionWarning: Data with input dtype int64, float64 were all converted to float64 by MinMaxScaler.
  return self.partial_fit(X, y)

	3	2.25	1670	6240	1	8	1240	430	1974	0	47.6413	-122.113
0	0.4	0.322581	0.306316	0.006023	0.4	0.7	0.343566	0.000000	0.730435	0.0	0.765001	0.401163
1	0.3	0.419355	0.294737	0.002854	0.4	0.6	0.330579	0.000000	0.930435	0.0	0.637393	0.429402
2	0.5	0.322581	0.264211	0.005423	0.4	0.6	0.296340	0.000000	0.773913	0.0	0.622513	0.316445
3	0.5	0.354839	0.173684	0.004190	0.0	0.4	0.095632	0.174274	0.600000	0.0	0.921236	0.288206
4	0.2	0.129032	0.041053	0.005750	0.0	0.4	0.046045	0.000000	0.504348	0.0	0.536956	0.166944

# 模型训练-简单线性回归
# 使用sklearn库的线性回归函数进行调用训练。梯度下降法获得误差最小值。最后使用均方误差法来评价模型的好坏程度，并画图进行比较。
from sklearn.linear_model import LinearRegression

LG = LinearRegression()
LG.fit(scaler_train_x,target)

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None,
         normalize=False)

# 使用均方误差用于评价模型好坏
from sklearn.metrics import mean_squared_error

LG_pre = LG.predict(scaler_train_x)
mse = mean_squared_error(LG_pre,target)
mse

48987685125.245766

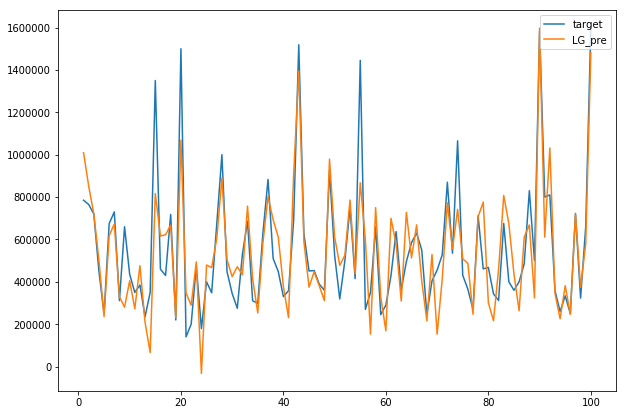
# 绘图进行比较
plot.figure(figsize=[10,7])
num = 100
x = np.arange(1,num+1)  # 取100个点进行比较
plot.plot(x,target[:num],label='target')
plot.plot(x,LG_pre[:num],label='LG_pre')
plot.legend(loc='upper right')
plot.show()

参考资料

一文通透优化算法：从随机梯度、随机梯度下降法到牛顿法、共轭梯度

一文看懂线性回归 网站还有各类算法通俗介绍

机器学习算法实践-标准与局部加权线性回归

LinearRegression

参数说明

sklearn.linear_model.LinearRegression(
fit_intercept=True #默认值为 True，表示计算随机变量，False 表示不计算随机变量

normalize=False #默认值为 False,表示在回归前是否对回归因子 X 进行归一化，True 表示是, copy_X=True)

LinearRegression 的属性有:coef_和 intercept_。coef_存储 w1 到 wp 的值，与 X 的维数一致。intercept_存储 w0 的值

from sklearn.linear_model import LinearRegression

x = [[0,1],[1,1],[2,2]]
y = [0,1,2]
clf = LinearRegression()
clf.fit(x,y)
print(clf.coef_)
print(clf.intercept_)
print(clf.predict([[3,3]]))
print(clf.score(x,y))

[1. 0.]
3.3306690738754696e-16
[3.]
1.0

Ridge Regression

from sklearn.linear_model import Ridge

Ridge回归（岭回归）

Ridge 回归用于解决两类问题:一是样本少于变量个数，二是变量间存在共线性,通过交叉验证来确定$alpha$ 的值

alpha=1.0 公式中$alpha$ 的值，默认为 1.0

max_iter=None #共轭梯度求解器的最大迭代次数

x = [[0,1],[1,1],[2,2]]
y = [0,1,2]
clf = Ridge()
clf.fit(x,y)
print(clf.coef_)
print(clf.intercept_)
print(clf.predict([[3,3]]))
print(clf.score(x,y))

[0.58333333 0.25      ]
0.08333333333333326
[2.58333333]
0.9097222222222223

用scikit-learn和pandas学习Ridge回归

RidgeCV:多个阿尔法，得出多个对应最佳的w,然后得到最佳的w及对应的阿尔法

from sklearn.linear_model import RidgeCV

x = [[0,1],[1,1],[2,2]]
y = [0,1,2]
clf = RidgeCV(alphas=[0.1,0.2,3,7,10,20])
clf.fit(x,y)
print(clf.coef_)
print(clf.intercept_)
print(clf.predict([[3,3]]))
print(clf.score(x,y))
print(clf.alpha_) # 表示0.1是上面几个中最好的

[0.87431694 0.16393443]
-0.09289617486341584
[3.02185792]
0.9958493833796188
0.1

Lasso Regression

估计稀疏系数的线性模型
适用于参数少的情况，因其产生稀疏矩阵，可用与特征提取

from sklearn.linear_model import Lasso

x = [[0,1],[1,1],[2,2]]
y = [0,1,2]
clf = Lasso(alpha=0.1)
clf.fit(x,y)
print(clf.coef_)
print(clf.intercept_)
print(clf.predict([[3,3]]))
print(clf.score(x,y))

[0.85 0.  ]
0.15000000000000002
[2.7]
0.9775

from sklearn.linear_model import LassoCV

x = [[0,1],[1,1],[2,2]]
y = [0,1,2]
clf = LassoCV(alphas=[0.1,0.2,1,2,5,7,10])
clf.fit(x,y)
print(clf.coef_)
print(clf.intercept_)
print(clf.predict([[3,3]]))
print(clf.score(x,y))

[0.85 0.  ]
0.15000000000000002
[2.7]
0.9775


/Users/zxx/anaconda3/lib/python3.7/site-packages/sklearn/model_selection/_split.py:2053: FutureWarning: You should specify a value for 'cv' instead of relying on the default value. The default value will change from 3 to 5 in version 0.22.
  warnings.warn(CV_WARNING, FutureWarning)