首先这是一道计数类DP,那我们得先推式子,经过瞎掰乱凑,经过认真分析,我们可以得到这样的方程
F(N)=F(0)+F(1)+....+F(N-M-1)
所有F初值为1,F(1)=2
ANS=F(N+M);
那显然我们有这样的代码:
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 const int M=1e9+7; 6 using namespace std; 7 inline int read(){ 8 char chr=getchar(); int f=1,ans=0; 9 while(!isdigit(chr)) {if(chr=='-') f=-1;chr=getchar();} 10 while(isdigit(chr)) {ans=(ans<<3)+(ans<<1);ans+=chr-'0';chr=getchar();} 11 return ans*f; 12 } 13 void write(int x){ 14 if(x<0) putchar('-'),x=-x; 15 if(x>9) write(x/10); 16 putchar(x%10+'0'); 17 }int n,m,f[10000005]; 18 int main(){ 19 n=read(),m=read(); 20 f[0]=1;f[1]=2; 21 for(int i=1;i<=n+m;i++){ 22 f[i]=1; 23 for(int j=0;j<=i-m-1;j++) 24 if(f[i]+f[j]>M) f[i]=f[i]+f[j]-M; 25 else f[i]=f[i]+f[j];//卡一波时间 26 }cout<<f[n+m]; 27 return 0; 28 }
显然这是O(n^2)的算法,然而面对N=1e18,这个算法可以去优化见鬼了,这样子由于语句比较简单,勉强可以过十万的数据大概30分
考虑优化:
我们先看一下上面的式子,尝试对这个式子变形...好吧,其实就是迭代,然后用鸽笼原理一通乱搞:
F(N)=F(N-1)+F(N-M-1)
ANS=F(N)
好了我们把这个东西优化得到了O(N)的算法:
期望得分:50pts
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 const int M=1e9+7; 6 using namespace std; 7 inline int read(){ 8 char chr=getchar(); int f=1,ans=0; 9 while(!isdigit(chr)) {if(chr=='-') f=-1;chr=getchar();} 10 while(isdigit(chr)) {ans=(ans<<3)+(ans<<1);ans+=chr-'0';chr=getchar();} 11 return ans*f; 12 } 13 void write(int x){ 14 if(x<0) putchar('-'),x=-x; 15 if(x>9) write(x/10); 16 putchar(x%10+'0'); 17 }int n,m,f[10000005]; 18 int main(){ 19 n=read(),m=read(); 20 f[0]=1;f[1]=2; 21 for(int i=2;i<=n;i++) 22 f[i]=(f[i-1]+f[max(i-m-1,0)])%M; 23 cout<<f[n]; 24 return 0; 25 }
考虑继续优化
某个大佬说过1e18的数据考虑logn的算法,比如快速幂。
这既然是DP,那自然往矩阵乘法考虑。
考虑构造矩阵:m这么小,而且递推式中出现的常量只有m,显然矩阵的大小要往m*m考虑
m=1的时候斐波那契,显然不用我推了
看一下其他情况: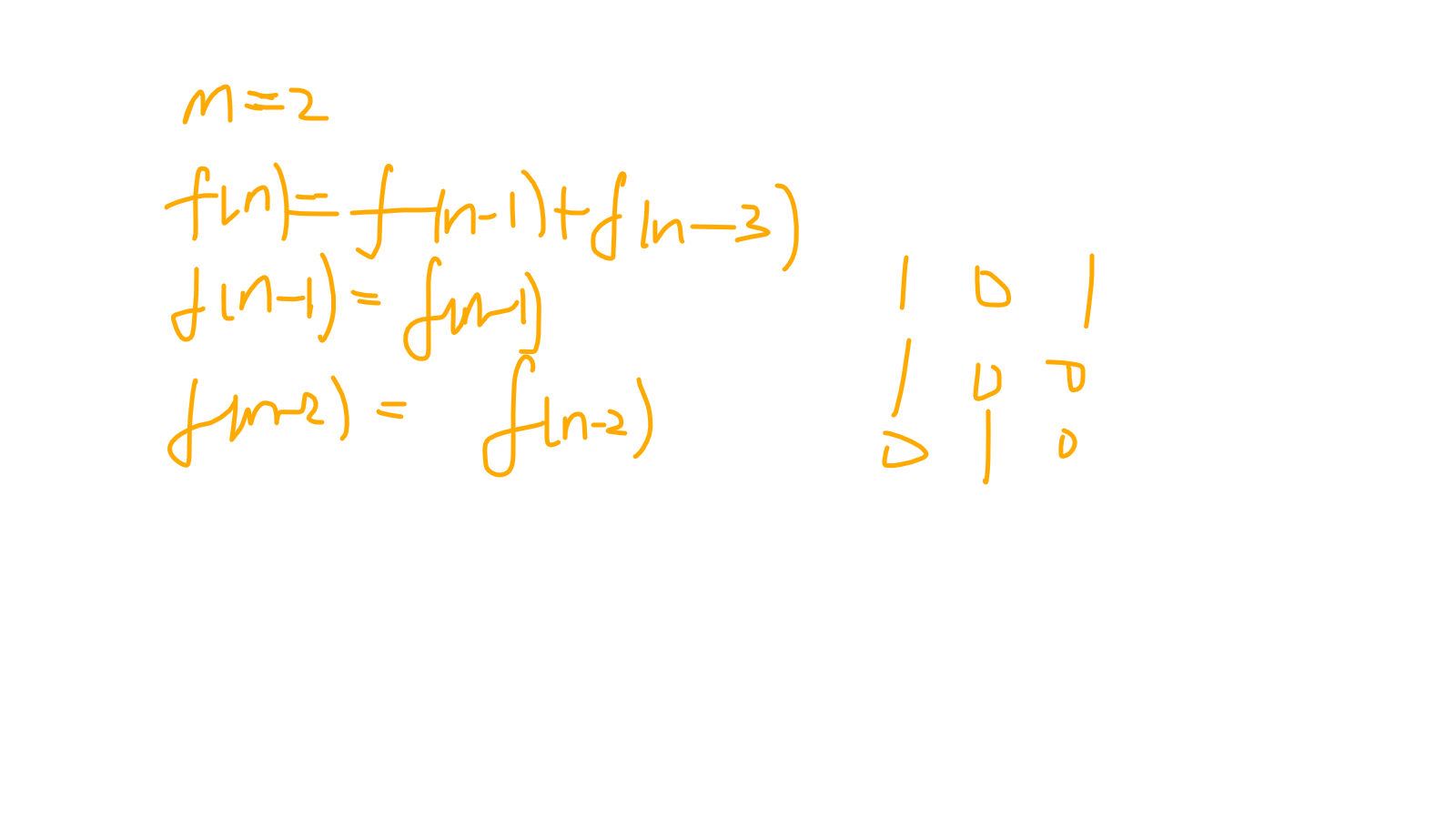

得到通式(写了的是1,其他是0):
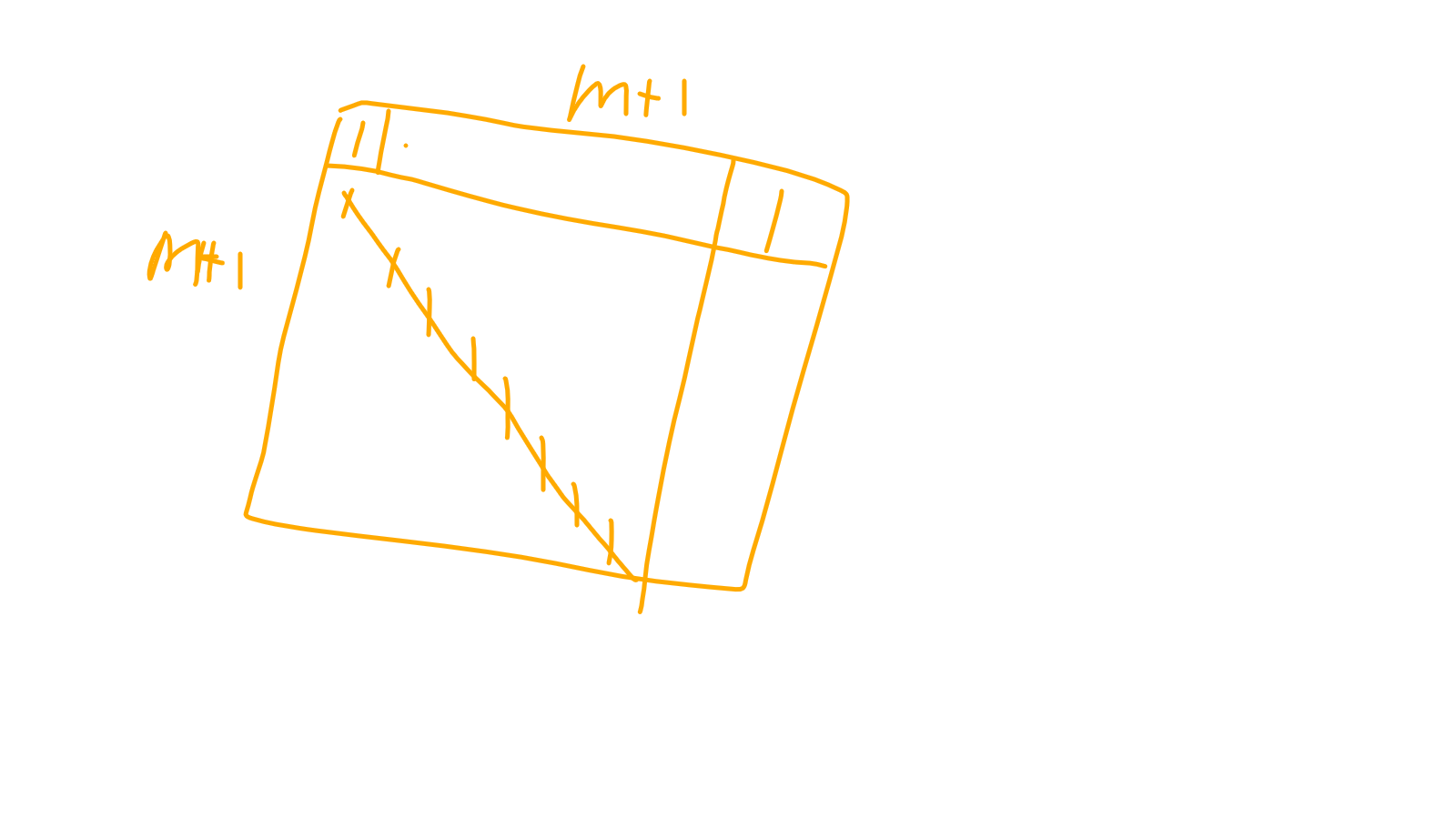
然后会矩阵加速的同学都知道该怎么做了吧...
1 // luogu-judger-enable-o2 2 #include<iostream> 3 #include<cstdio> 4 #include<cstring> 5 #include<algorithm> 6 #define int long long 7 const int M=1e9+7; 8 using namespace std; 9 inline int read(){ 10 char chr=getchar(); int f=1,ans=0; 11 while(!isdigit(chr)) {if(chr=='-') f=-1;chr=getchar();} 12 while(isdigit(chr)) {ans=(ans<<3)+(ans<<1);ans+=chr-'0';chr=getchar();} 13 return ans*f; 14 } 15 void write(int x){ 16 if(x<0) putchar('-'),x=-x; 17 if(x>9) write(x/10); 18 putchar(x%10+'0'); 19 }int n,m; 20 struct P{int a[20][20];P(){memset(a,0,sizeof(a));}}A,B; 21 P operator *(const P &x,const P &y){ 22 P ans; 23 for(int i=0;i<m;i++) 24 for(int k=0;k<m;k++) 25 for(int j=0;j<m;j++) 26 ans.a[i][j]=(ans.a[i][j]+x.a[i][k]*y.a[k][j])%M; 27 return ans; 28 } 29 void KSM(int n){ 30 while(n){ 31 if(n&1) B=B*A; 32 n>>=1;A=A*A; 33 } 34 } 35 inline void init(){ 36 n=read(),m=read();--n,++m; 37 A.a[m-1][m-1]=A.a[0][m-1]=1; 38 for(int i=0;i<m-1;i++) A.a[i+1][i]=1;//初始矩阵 39 for(int i=0;i<m;i++)B.a[0][i]=i+2; 40 } 41 signed main(){ 42 init();KSM(n); 43 write(B.a[0][0]); 44 return 0; 45 }