不难的一道题,就是码的时候出了点问题,看了其他巨佬的题解才发现问题所在...
题目大意:
给定一个有向图,n个点,m条边。请问,1号点到2号点有多少条路径?如果有无限多条,输出inf,如果有限,输出答案模1e9的余数。
首先是0的情况:
不存在1~2的路径,即图不一定联通(不这样特判也可以,但是常数会小一点)
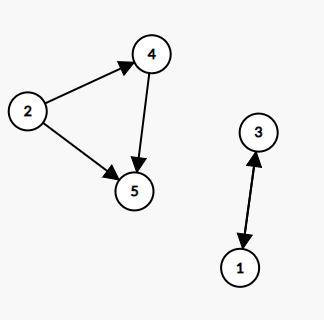
其次是inf的情况:
如果在1~2的某条路径中存在某个点属于某个强连通分量,那么这条路径就可以在这个强连通分量里无限走下去,答案就是inf
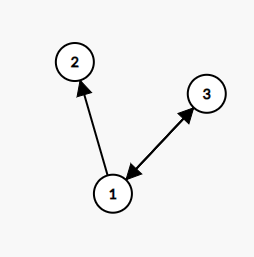
一般情况:
如果这条路径不属于第二种情况,那就考虑计数吧...
我们可以用一个dp数组计数,然后乱搞BFS即可,不用考虑是否vis,因为排除了第二种情况后显然是不会过度访问(RE)的
同时我们可以记录每一个节点的入度个数,在最后BFS,DP的时候,根据入度可以减少判断很多情况
同时:一个小问题:在考虑情况2的时候,我们需要建立反向边,以便判断1,2可达性(刚开始想当然了这个没判)
1 #pragma GCC optimize("Ofast") 2 #pragma GCC optimize(3) 3 #include<cstdio> 4 #include<iostream> 5 #include<cstring> 6 #include<queue> 7 #define ha 1000000000 8 using namespace std; 9 inline int read(){ 10 int ans=0,f=1;char chr=getchar(); 11 while(!isdigit(chr)){if(chr=='-') f=-1;chr=getchar();} 12 while(isdigit(chr)){ans=(ans<<3)+(ans<<1)+chr-48;chr=getchar();} 13 return ans*f; 14 }void write(int x){ 15 if(x<0) putchar('-'),x=-x; 16 if(x>9) write(x/10); 17 putchar(x%10+'0'); 18 }const int M=1e5+5; 19 int head[M],head1[M],ver1[M],nxt1[M],ver[M],nxt[M],tot,n,m,vis1[M],vis2[M],dfn[M],low[M],ins[M],sta[M],top,t,col,color[M],cnt[M],tot1,dp[M],in[M]; 20 inline void add(int x,int y){ver[++tot]=y;nxt[tot]=head[x];head[x]=tot;} 21 inline void add1(int x,int y){ver1[++tot1]=y;nxt1[tot1]=head1[x];head1[x]=tot1;} 22 void dfs1(int x){for(int i=head[x];i;i=nxt[i])if(in[ver[i]]++,!vis1[ver[i]])dfs1(ver[vis1[ver[i]]=1,i]);} 23 void dfs2(int x){for(int i=head1[x];i;i=nxt1[i])if(!vis2[ver1[i]])dfs2(ver1[vis2[ver1[i]]=1,i]);} 24 inline bool check_LT(){vis2[2]=1,dfs2(2);if(vis1[vis1[1]=1,dfs1(1),2]) return 0;return 1;} 25 void Tarjan(int x){ 26 sta[top++]=x;low[x]=dfn[x]=++t;ins[x]=1; 27 for(register int i=head[x];i;i=nxt[i]) 28 if(ins[ver[i]]==1) low[x]=min(low[x],dfn[ver[i]]); 29 else if(ins[ver[i]]==0) low[x]=min(low[Tarjan(ver[i]),x],low[ver[i]]); 30 low[x]==dfn[x]?++col:col; 31 if(low[x]==dfn[x])do{--top,color[sta[top]]=col,ins[sta[top]]=-1,++cnt[col];}while(sta[top]!=x); 32 }queue<int> q; 33 void BFS(){ 34 q.push(1);dp[1]=1; 35 while(!q.empty()){ 36 int x=q.front();q.pop(); 37 for(register int i=head[x];i;i=nxt[i]){ 38 if(!vis1[ver[i]]) continue; 39 dp[ver[i]]=(dp[ver[i]]+dp[x])%ha; 40 if(!--in[ver[i]]) q.push(ver[i]); 41 } 42 } 43 } 44 int main(){ 45 n=read(),m=read(); 46 for(register int i=1,x,y;i<=m;++i) x=read(),y=read(),add(x,y),add1(y,x); 47 if(check_LT()){return puts("0"),0;} 48 for(register int i=1;i<=n;++i) if(!dfn[i]) Tarjan(i); 49 for(register int i=1;i<=n;++i) 50 if(vis1[i]&&vis2[i]&&cnt[color[i]]>=2) 51 return puts("inf"),0; 52 return BFS(),write(dp[2]),0; 53 }