(不过个人感觉我讲的稍微更清楚一点)
题目就是让我们求图中满足数值大于等于B的连通块数量
然后我们可以尝试转换为求连通块两端所产生的“谷”的数量,显然一个连通块对谷可以贡献2的答案,最终答案就是谷的数量除以2
(下图为查询$B_i$大小为4时的情况,每一个箭头代表一个谷)
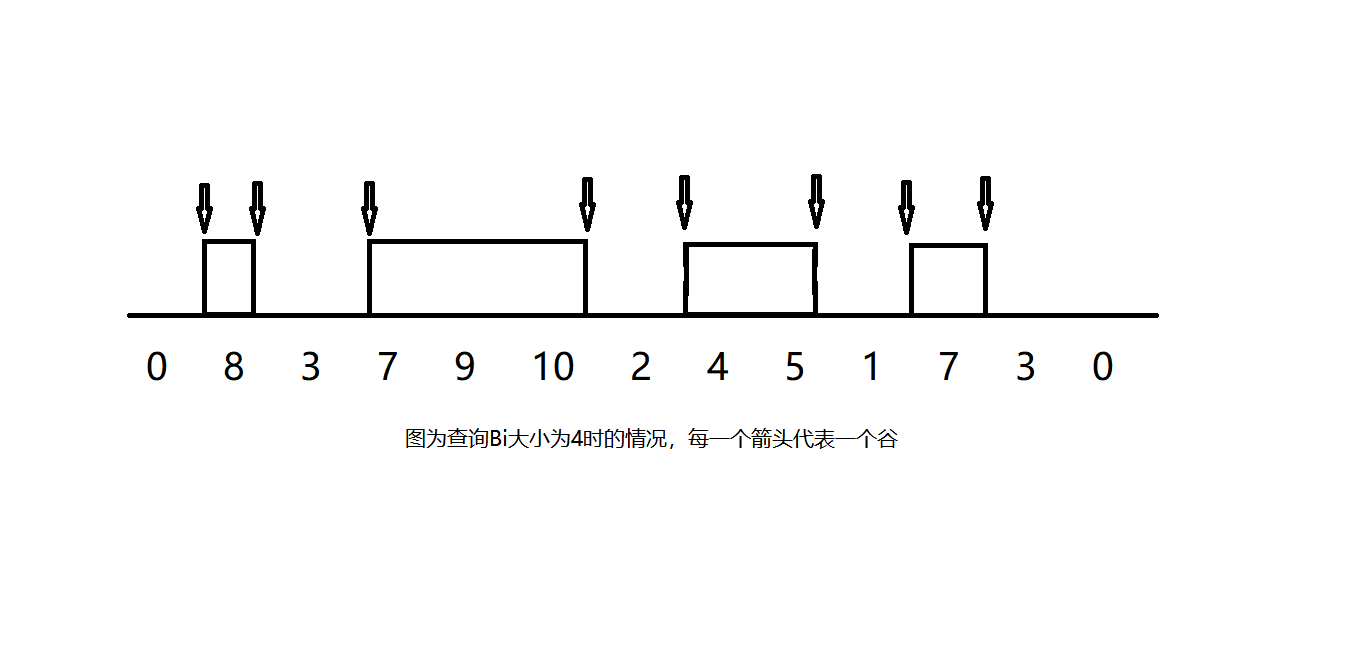
发现每两个数中间的空格都是有可能产生谷的,所以我们只需要维护有多少个空格满足产生谷的条件即可
记一个空格左边的数字为X,右边的数字为Y,当前询问为B,观察发现,当且仅当满足下列条件时,这个空格可以成为谷
$$min(X,Y)+1 leq B leq max(X,Y)$$
我们需要一种可以在$logn$的复杂度内维护满足上述条件点的数量,支持单点修改区间查询的数据结构,发现树状数组可以很好的满足这个要求、
我们把这个询问条件差分一下扔到树状数组里维护即可
一些注意点:
开始更新的时候要把0和n+1这两个节点也算进去,以免漏记录两端的“谷”
观察到$a_i$,$b_i$很大,我们需要进行必要的离散化
代码:
1 //hgs AK IOI,IMO,ICHO,IPHO 2 #include<bits/stdc++.h> 3 #define writeln(x) write(x),puts("") 4 #define writep(x) write(x),putchar(' ') 5 using namespace std; 6 inline int read(){ 7 int ans=0,f=1;char chr=getchar(); 8 while(!isdigit(chr)){if(chr=='-') f=-1;chr=getchar();} 9 while(isdigit(chr)){ans=(ans<<3)+(ans<<1)+chr-48;chr=getchar();} 10 return ans*f; 11 }void write(int x){ 12 if(x<0) putchar('-'),x=-x; 13 if(x>9) write(x/10); 14 putchar(x%10+'0'); 15 }const int M= 6e5+5; 16 int s[M],n,m,x,y,z,b[M],len,v[M]; 17 struct P{int opt,x,y;}q[M]; 18 #define low(x) (x&-x) 19 inline int GetNum(int x){return lower_bound(b+1,b+len+1,x)-b;} 20 inline void Update(int x,int y){for(++x;x<=n*3;x+=low(x))s[x]+=y;} 21 inline int Query(int x){int ans=0;for(++x;x;x-=low(x))ans+=s[x];return ans;} 22 inline void Init(){int tot=0;//离散化 + 树状数组初始化 23 for(int i=1;i<=n;i++)b[++tot]=v[i]; 24 for(int i=1;i<=m;i++)if(q[i].opt==1)b[++tot]=q[i].x;else b[++tot]=q[i].y; 25 sort(b+1,b+tot+1),len=unique(b+1,b+tot+1)-b-1; 26 for(int i=1;i<=n;i++)v[i]=GetNum(v[i]); 27 for(int i=1;i<=m;i++)if(q[i].opt==1)q[i].x=GetNum(q[i].x);else q[i].y=GetNum(q[i].y); 28 for(int i=1;i<=n+1;i++){ 29 int l=v[i-1],r=v[i]; 30 if(l>r)swap(l,r); 31 Update(++l,1),Update(++r,-1); 32 } 33 } 34 inline void Add(int x,int y){ 35 int l=v[x-1],r=v[x]; 36 if(l>r)swap(l,r); 37 Update(++l,y),Update(r+1,-y); 38 l=v[x],r=v[x+1]; 39 if(l>r)swap(l,r); 40 Update(++l,y),Update(r+1,-y); 41 } 42 inline void Solve(){ 43 for(int i=1;i<=m;i++) 44 if(q[i].opt==1)printf("%d ",Query(q[i].x)/2); 45 else Add(q[i].x,-1),v[q[i].x]=q[i].y,Add(q[i].x,1); 46 } 47 int main(){ 48 n=read(),m=read(); 49 for(int i=1;i<=n;i++)v[i]=read(); 50 for(int x,y,z,i=1;i<=m;i++){ 51 if((x=read())==1)q[i].opt=1,q[i].x=read(); 52 else q[i].opt=2,q[i].x=read(),q[i].y=read(); 53 }Init();Solve(); 54 return 0; 55 }