算法目的:对一个正整数分解质因数
一、算法分析:
1、建立整数列表,保存求到的因数。
2、声明整数i=2,用以递增取模;整数m,用于临时保存n
3、建立while循环,i小于等于整数m时,判断m%i,如果等于0,可以被整除,则令 m = m/i 将 i添加到 整数列表;如果m%i不等于0,i++
4、判断整数列表长度,如果长度为1,则认定n是质数;否则为合数并打印列表
5.加入n的开方值比较,如果i 递增到n的开方值但整数列表的大小仍为0,则认为此数是质数
二、运算结果抢先看
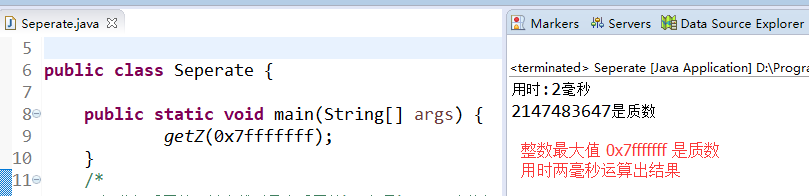
三、基础程序
package fundamental; import java.util.ArrayList; import java.util.List; public class Seperate { public static void main(String[] args) { getZ(102039); } /* 对n分解质因数,首先找到最小质因数k,如果k==n,直接打印退出。 n<>k,继续k+1对n进行分解 */ public static void getZ(int n){ List<Integer> l = new ArrayList<Integer>(); int i = 2,m = n; long start = System.currentTimeMillis(); while(i<=m){ // i<=m 与 i<=n 在运算合数时,效率差很多 if(m%i==0){ m=m/i; l.add(i); }else i++; } long end = System.currentTimeMillis(); // 0x7fffffff 是 质数,所以i值会累加到 0x7fffffff,比较耗时。但不会超过9秒,因为i值最多累加到0x7fffffff // 运算时长与n值大小无关,与最大因数有关。 // 最大因数越大,运算越慢,反之越快。 System.out.println("用时:"+(end-start)+"毫秒"); if(l.size()==1) System.out.println(n+"是质数"); else System.out.println(l.toString()); } }
四、优化算法
加入开方值比较,减少时间复杂度
package fundamental; import java.util.ArrayList; import java.util.List; public class Seperate { public static void main(String[] args) { getZ(0x7fffffff); } /* 对n分解质因数,首先找到最小质因数k,如果k==n,直接打印退出。 n<>k,继续k+1对n进行分解 */ public static void getZ(int n){ List<Integer> l = new ArrayList<Integer>(); int i = 2,m = n; long start = System.currentTimeMillis(); // sqrt 用以减少比较时间 int sqrt = (int) Math.sqrt(n); while(i<=m ){ // i<=m 与 i<=n 在运算合数时,效率差很多 if(m%i==0){ m=m/i; l.add(i); }else i++; /* 以下一行是优化算法: 如果 i 超过 sqrt 还没有因数存在,则认为是质数,跳出循环 因为 n 如果是两个质数的乘积,i值需要递增到sqrt才能判断出n是否为质数 */
if(i>sqrt) {
if(l.size()==0) System.out.println(n+"是质数");
else l.add(m);
break;
} } long end = System.currentTimeMillis(); // 0x7fffffff 是 质数,所以i值会累加到 0x7fffffff,比较耗时。但不会超过9秒,因为i值最多累加到0x7fffffff // 运算时长与n值大小无关,与最大因数有关。 // 最大因数越大,运算越慢,反之越快。 System.out.println("用时:"+(end-start)+"毫秒"); if(l.size()==0) System.out.println(n+"是质数"); else System.out.println(l.toString()); } }