分治思想：合并排序和快速排序

分治思想：合并排序和快速排序

　　分治思想(Divide-and-conquer):

　　作为程序设计的一种方法，有时为了解决一个给定的问题，算法要一次或多次地递归调用自身来解决相关的子问题。这些算法通常采用分子的策略：将一个问题划分成n个规模更小并且结构和原问题相似的子问题；递归地解决这些子问题，然后再合并其结果，就得到原问题的解。

　　一般采用分治方法解决问题，按如下三个步骤不断循环：

• 分解(  Divide  ): 将原问题分解成许多个规模更小并且和原问题结构相似的小问题
• 控制(Conquer): 从小问题的层次上着手解决问题。(在递归层面上:1. 小问题如何解决 2. 做下一层递归的条件如何设置)
• 合并(Combine): 将子问题得到的解如何归并成原问题的解。

　　快速排序(Quick sort)

　　基本思想:

　　选择一个数组中一个元素作为主元(pivot), 以该主元作为标杆将数组的元素分为大于(或大于等于)主元和小于(或小于等于)主元的两部分(区分的同时也进行位置调换操作)。这时形成的两个子数组在结构形式上和原数组相同，再寻找它们的主元，以此再分。如此不断循环，原数组被分割成许多小数组，当小数组的元素小于等于三个时，按照分割的标准这时已经形成了有序的排列。当这些小数组有序时，合并形成的大数组就是有序的。

　　用分治的思想描述(从小到大排序):

　　分解: 选择一个主元A[p], 将数组A[p,..r]划分成两个子数组A[p,..q-1]和A[q+1,..r](通过原地操作实现位置调换), 使得A[p,..q-1]全部小于等于A[p]和A[q+1,..r]全部大于等于A[p]，下标p也在这个划分过程中计算。

　　控制：通过递归调用，对两个子数组排序

　　合并：因为两个子数组是就地排序，对他们进行合并不需要操作，整个数组已实现排序。

　　复杂度：

　　最佳情况：每次划分形成子数组的大小都相同或者相差一个，这时时间复杂度为O(nlgn)

　　最坏情况：每次划分形成的子数组大小为1和n-1，这时时间复杂度为Θ(x²)。

　　快速排序的C代码如下：

　　

void swap(int *a,int *b)
{
    int temp;
    temp=*a;
    *a=*b;
    *b=temp;
}

int partiotion(int A[],int p,int r)
{
    int pivot;
    int i,j;

    /**   划分数组的数随机产生版本
    int randnum;
    //使用时间作为随机种子
    srand(time(NULL));

    //产生p-r之间的随机数
    randnum=rand()%(r-p)+p;

    swap(&A[randnum],&A[r]);
    **/
    pivot=A[r];

    i=p-1;

    for(j=p;j<r;j++)
        if(A[j]<=pivot)
        {
            i=i+1;
            swap(&A[i],&A[j]);
        }

    swap(&A[i+1],&A[r]);
        
    return i;
}

void quickSort(int A[],int p, int r)
{
    int temp;

    if(p<r)
    {
        temp=partiotion(A,p,r);
        //划分成2个子数组，再使用递归调用
        quickSort(A,p,temp);
        quickSort(A,temp+1,r);
    }

}

　　合并排序(Merge Sort)：

　　基本思想：

　　对两个已经排序的数组，合并成一个有序的数组时间复杂度为θ(n)和 n 个额外的存储空间。对一个数组排序，首先将数组划分成单个元素，两两实行合并，再对合并形成的小数组合并，如此不断循环。如图1 实例所示：

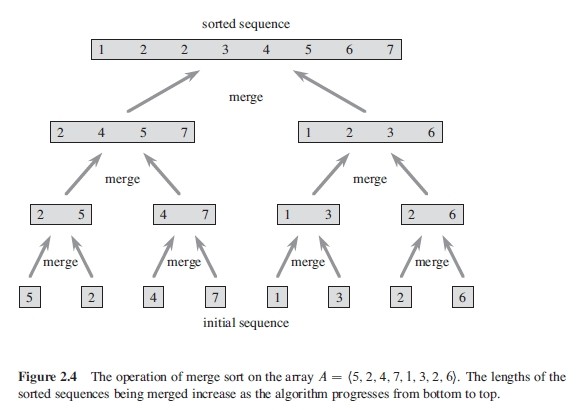
图 1. 合并排序的一个实例(图片来源《算法导论》)

　　分治思想(从小到大排序)：

　　分解：将原数组化分成两个子数组

　　控制：将子数组实现合并到一个数组形成有序序列

　　合并：采用递归调用时，将上次合并的结果作为这次的输入。由于递归最底层的数组大小为1， 可以确保两个数的合并是有序的。这样每次递归调用返回的结果也是有序的。最终形成的数组自然是有序的。

　　复杂度：输入的结果对时间复杂度影响不大，只和排序的规模有关。时间复杂度为Θ(nlgn)。另外需要O(n)个额外的存储空间。

　　合并排序的代码如下(从小到大)：　　

void combine(int A[],int p, int q, int r)
{
    
    int *temp1;
    int *temp2;
    int i,j,k;

    temp1=(int *)malloc(sizeof(int)*(q-p+2));
    temp2=(int *)malloc(sizeof(int)*(r-q+2));

    //注意子数组的长度
    for(i=0;i<q-p;i++)
    {
        temp1[i]=A[p+i];
    }

    //哨兵元素：很巧妙，本来应该设置一个无限大的数，这里只取一个实数
    temp1[i]=357834;
    
    for(j=0;j<r-q+1;j++)
    {
        temp2[j]=A[q+j];
    }

    //哨兵元素
    temp2[j]=357834;

    i=0;
    j=0;

    for(k=p;k<=r;k++)
        if(temp1[i]<temp2[j])
        {
            A[k]=temp1[i];
            i++;
        }
        else
        {
            A[k]=temp2[j];
            j++;
        }

}



void mergeSort(int A[],int p,int q)
{
    if(p<q)
    {
        int pi=(int)((p+q)/2);
        mergeSort(A,p,pi);
        mergeSort(A,pi+1,q);

        combine(A,p,pi+1,q);
    }

}

　　合并排序和快速排序递归差异：

　　合并排序递归是通过将更深一层次递归的结果作为这一次的输入（上浮），而快速排序递归是将这次操作为下次递归做准备，作为下次操作的输入（下沉）。