zoukankan html css js c++ java

文件压缩与解压：霍夫曼编码

文件压缩与解压：霍夫曼编码

　　由于计算机的存储空间，文件传输时间成本等条件的限制，产生了对文件进行压缩从而减少文件大小的需求，各种压缩算法及其技术应运而生。其中的霍夫曼编码作为无损压缩当中最好的方法，受到了广泛的应用。

　　霍夫曼编码(Huffman Coding)：

　　霍夫曼编码是一种无损压缩算法，于1952年由Divid A. Huffman在其博士论文《A Method for the Construction of Minimum-Redundancy Codes》提出。基本原理是利用二进制位代替原先字符进行存储，减少文件计算机存储的总位数从而减少文件的大小。下面用一个实例来说明其原理。

　　实例：

　　输入一个文本文件，根据Huffman算法原理对文件进行压缩，将压缩后的所有字符输入到另外一个文件上。

　　注意：实际要对文件进行压缩需要使用二进制的方式读取文件，构造Huaffman树，接着求出每个字符对应的Huffman编码，得到的编码是二进制是0和1,，而非字符型的0和1。为了说明Huffman编码的原理在本文中我使用的是字符型的0和1（下面会有解释说明）。

　　Huffman 编码是一种前缀编码，即频率越高的字符对应的编码长度越短。相对于等长度的编码来讲，大多数情况下总编码长度要短的多。对上文给的实例，其实现主要有以下几个步骤：

遍历所有字符

　　遍历文件所有的字符，并统计文件中不相同的字符即其出现的个数。

　　代码如下：　

 1 /**
 2     读取文本文件，遍历文件中所有的字符，统计每个字符出现的频率，将字符和其对应的频数存储
 3     在huffmantable结构体中，并且返回不同字符的个数
 4 **/
 5 int readfile(char *filename,huffmantable *node)
 6 {
 7 
 8     char temp;
 9     int length,i;
10     FILE *file;
11     errno_t err;
12 
13     length=0;
14 
15     err=fopen_s(&file,filename,"r");
16 
17     if(err!=0)
18     {
19         printf("the file can not open!
");
20     }
21     else
22     {
23         while((temp=fgetc(file))!=EOF)
24         {
25             if(length==0)
26             {
27                 node[0].character=temp;
28                 node[0].count=1;
29                 length++;
30                 
31             }
32             else
33             {
34                 for(i=0;i<length;i++)
35                 {
36                     if(node[i].character==temp)
37                     {
38                         
39                         node[i].count=node[i].count+1;//特别注意node.count没有初始化
40                         break;                          //break:执行break后不执行其后的语句
41                     }
42                 }
43                     if(i==length)
44                     {
45                         node[length].character=temp;
46                         node[length].count=1;
47                         length++;
48                     }
49             }            
50         }
51     }
52 
53     fclose(file);
54     return length;
55 }

读取文件，遍历字符

　　2. 生产霍夫曼树

　　对于怎样产生霍夫曼树，引用算法导论的实例。如下图所示：

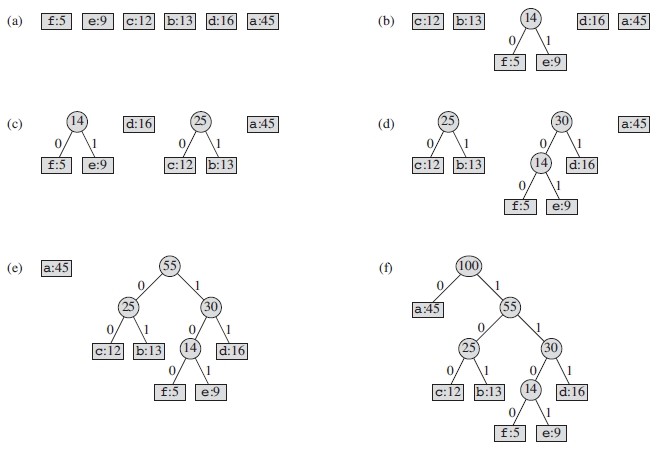
图片来源：《算法导论》

　　从该图中可以看到，这是一棵满二叉树，所有的字符信息都存储在叶子节点中，而且出现次数越小的字符越底层，即对应的路径就越长，这和频繁度越高编码越短的原则是一致的。这样总编码长度应该是所有树种最优的。

　　前缀编码：前缀编码是指任何一个字符的编码都不是其他字符编码的前缀。霍夫曼编码一定是前缀编码的原因：在霍夫曼树种没有一个字符所在的节点是其他字符的父节点。

　　代码如下：

 1 //从所有未加入霍夫曼树中选择频率最小的字符
 2 int chooseMin(huffmantable *priTree, int length)
 3 {
 4     //huffmantable temp;
 5     int min=6555334;
 6     int minpoint=0;
 7     int i;
 8 
 9     for(i=0;i<length;i++)
10         if(priTree[i].count!=-2  && priTree[i].count<min  )
11         {
12             min=priTree[i].count;
13             minpoint=i;
14         }    
15         
16         return minpoint;
17         
18 }
19 
20 /*  构建霍夫曼树  */
21 huffmantable *createHuffmanTree(huffmantable *node, int length)
22 {
23     int i;
24     int m;
25     int Fmin,Smin;
26     int count1;
27     int count2;
28 
29     huffmantable *priArray;
30 
31     //霍夫曼树中节点总数
32     m=2*length-1;
33 
34     //对结构体数组进行扩充
35     priArray=(huffmantable *)malloc(sizeof(huffmantable)*m);
36 
37     //复制读取文件后取得信息到新数组
38     for(i=0;i<length;i++)
39     {
40         //memcpy(&priArray[i],&node[i],sizeof(huffmantable));
41         priArray[i].character=node[i].character;
42         priArray[i].count=node[i].count;
43         priArray[i].lchild=-1;
44         priArray[i].rchild=-1;
45         priArray[i].parent=-1;
46         //priArray
47     }
48 
49     //对非叶子节点进行初始化操作
50     for(i=length;i<m;i++)
51     {
52         priArray[i].count=-1;
53         priArray[i].lchild=-1;
54         priArray[i].rchild=-1;
55         priArray[i].parent=-1;
56     }
57 
58     
59 
60     for(i=0;i<length-1;i++)
61     {
62         //选择第一小频率节点，
63         Fmin=chooseMin(priArray,length+i);
64         count1=priArray[Fmin].count;
65         priArray[Fmin].count=-2;
66         
67         //选择第二小频率节点
68         Smin=chooseMin(priArray,length+i);
69         count2=priArray[Smin].count;
70         priArray[Smin].count=-2;
71         
72         //分别链接到左子节点和右子节点
73         priArray[length+i].lchild=Fmin;
74         priArray[length+i].rchild=Smin;
75         priArray[length+i].count=count1+count2;
76         
77         
78         
79         
80         priArray[Fmin].parent=length+i;
81         priArray[Smin].parent=length+i;
82     }
83 
84     return priArray;
85 
86 }

构造霍夫曼树

　　3. 进行编码

　　按照生成的霍夫曼树按照左0右1的原则，从根节点开始到每个叶子节点所走的路径形成的二进制序列即为霍夫曼编码。

 1 /**
 2     对已经构建好了霍夫曼树（以二叉链表形式存储）遍历，生成霍夫曼编码
 3 **/
 4 huffmancode *huffmancoding(int length,huffmantable *priarray)
 5 {
 6     huffmancode *coding;
 7     char *temp;
 8     int i;
 9     int clen;
10     int m;
11 
12     coding=(huffmancode *)malloc(sizeof(huffmancode)*length);
13     temp=(char *)malloc(sizeof(char)*length);
14 
15     for(i=0;i<length;i++)
16     {
17         coding[i].character=priarray[i].character;
18     }
19 
20 
21     for(i=0;i<2*length-1;i++)
22     {
23         priarray[i].count=0;
24     }
25 
26     m=2*length-2;
27     
28     clen=0;
29 
30     /* 采用DFS算法进行遍历： 0表示未遍历状态；1表示遍历了左子节点，未遍历右子节点；2 表示遍历了双节点 */
31     while(m!=-1)
32     {
33         if(priarray[m].count==0)
34         {
35             priarray[m].count=1;
36             if(priarray[m].lchild!=-1)
37             {    
38                 
39                 m=priarray[m].lchild;
40                 temp[clen++]='0';
41             }
42             else 
43             {
44                 coding[m].codeString=(char *)malloc(sizeof(char)*clen);
45                 for(i=0;i<clen;i++)
46                 {
47                     coding[m].codeString[i]=temp[i];    
48                 }
49                 coding[m].codeString[clen]='';//表面该叶子节点的字符对应的编码序列结束
50 
51             }
52             
53         }
54         else if( priarray[m].count==1)
55         {
56             priarray[m].count=2;
57             if(priarray[m].rchild!=-1)
58             {
59                 
60                 m=priarray[m].rchild;
61                 temp[clen++]='1';
62             }
63         
64         }
65         else
66         {
67             priarray[m].count=0;
68             m=priarray[m].parent;
69             --clen;
70         }
71 
72     }
73 
74     return coding;
75 }

依据霍夫曼树生产霍夫曼编码

　　4. 霍夫曼编码替换字符

　　上文讲过，为了展现霍夫曼编码原理，该实例中我们用字符型的0和1替代二进制位的0和1，所以我们程序中使用的就是每个字符对应的字符型编码输入到另外一个文件中。(一个字符型的'0' 或者 '1' 有8位二进制的0或者1 组成，而文本文件中一个字符也对应8位，汉字对应2个字符即16位，如果我们用字符型的 '0' 和 '1' 表示霍夫曼编码实际上将字符长度扩充了8倍，所以实际用霍夫曼编码算法实现压缩不会像下文的程序中所示（但原理基本一样），而是使用二进制的0和1)。

　　代码如下：

 1 /**
 2     使用两个文件操作符，一边读取字符，一边对照霍夫曼编码将对应的编码输入到另一个文件中    
 3 **/
 4 
 5 void zipfunc(huffmancode *code,int length)
 6 {
 7     FILE *wcpp,*rcpp;
 8     errno_t err1,err2;
 9     char temp;
10     int i;
11 
12     err1=fopen_s(&wcpp,"zip.txt","w");
13     err2=fopen_s(&rcpp,"test.txt","r");
14 
15     if(err2!=0)
16     {
17         printf("The resourse file can not be found
!");
18     }
19     else
20     {
21         if(err1!=0)
22         {
23             printf("The write file can not be found!
");
24         }
25         else
26         {
27             while((temp=fgetc(rcpp))!=EOF)
28             {
29                 for(i=0;i<length;i++)
30                     if(code[i].character==temp)
31                         break;
32                 fprintf(wcpp,"%s",code[i].codeString);
33             }
34         }
35 
36     }
37     fclose(wcpp);
38     fclose(rcpp);
39 }

对文件进行压缩操作

　　霍夫曼解码

　　有压缩必然有解压操作。霍夫曼解码的原理很简单：将文件中形成霍夫曼编码序列和霍夫曼树对应，从树的根结点开始，如果为0则转导左子节点，如果为1 则转到右子节点，一直按照这样的对应关系进行操作，直到遇到霍夫曼树的叶子结点，将叶子结点中的字符输出，再定位到树的根结点开始遍历，如此反复，直到文件中霍夫曼编码序列遍历完为止。

　　代码如下：

 1 void unzipfunc(huffmantable *codetable,int length)
 2 {
 3     FILE *rcpp,*wcpp;
 4     errno_t err1,err2;
 5     int tempnode;
 6     char temp;
 7     int i;
 8 
 9     
10 
11     err1=fopen_s(&rcpp,"zip.txt","r");
12     err2=fopen_s(&wcpp,"unzip.txt","w");
13 
14 
15     if(err1!=0)
16     {
17         printf("The resource file can not be open!
");
18     }
19     else
20     {
21         tempnode=length-1;
22         while((temp=fgetc(rcpp))!=EOF)
23         {
24             //temp=fgetc(rcpp);
25             if(temp=='0')
26             {
27                 tempnode=codetable[tempnode].lchild;
28             }
29             else if(temp=='1')
30             {
31                 tempnode=codetable[tempnode].rchild;
32             }
33             if(codetable[tempnode].lchild==-1 && codetable[tempnode].rchild==-1 )
34             {
35                 fputc(codetable[tempnode].character,wcpp);
36                 tempnode=length-1;
37             }
38             
39 
40         }
41     }
42     fclose(wcpp);
43     fclose(rcpp);
44 
45 }

霍夫曼解码

　　整个实例的实现代码如下：

  1 #include <stdio.h>
  2 #include <tchar.h>
  3 #include <stdlib.h>
  4 #include <string.h>
  5 
  6  struct huffmantable
  7 {
  8     char character;
  9     int count;
 10     int parent;
 11     int lchild;
 12     int rchild;
 13 };
 14 
 15  struct huffmancode
 16  {
 17      char character;
 18      char *codeString;
 19  };
 20 
 21 char *stringdata=NULL;
 22 long Length;
 23 
 24 
 25 int chooseMin(huffmantable *priTree, int length);
 26 int readfile(char *filename,huffmantable *node);
 27 huffmantable *createHuffmanTree(huffmantable *node, int length);
 28 huffmancode *huffmancoding(huffmantable *priTree,int length,huffmantable *priarray);
 29 int chooseMin(huffmantable *priTree, int length);
 30 
 31 /**
 32     读取文本文件，遍历文件中所有的字符，统计每个字符出现的频率，将字符和其对应的频数存储
 33     在huffmantable结构体中，并且返回不同字符的个数
 34 **/
 35 int readfile(char *filename,huffmantable *node)
 36 {
 37 
 38     char temp;
 39     int length,i;
 40     FILE *file;
 41     errno_t err;
 42 
 43     length=0;
 44 
 45     err=fopen_s(&file,filename,"r");
 46 
 47     if(err!=0)
 48     {
 49         printf("the file can not open!
");
 50     }
 51     else
 52     {
 53         while((temp=fgetc(file))!=EOF)
 54         {
 55             if(length==0)
 56             {
 57                 node[0].character=temp;
 58                 node[0].count=1;
 59                 length++;
 60                 
 61             }
 62             else
 63             {
 64                 for(i=0;i<length;i++)
 65                 {
 66                     if(node[i].character==temp)
 67                     {
 68                         
 69                         node[i].count=node[i].count+1;//特别注意node.count没有初始化
 70                         break;                          //break:执行break后不执行其后的语句
 71                     }
 72                 }
 73                     if(i==length)
 74                     {
 75                         node[length].character=temp;
 76                         node[length].count=1;
 77                         length++;
 78                     }
 79             }            
 80         }
 81     }
 82 
 83     fclose(file);
 84     return length;
 85 }
 86 
 87 
 88 
 89 //从所有未加入霍夫曼树中选择频率最小的字符
 90 int chooseMin(huffmantable *priTree, int length)
 91 {
 92     //huffmantable temp;
 93     int min=6555334;
 94     int minpoint=0;
 95     int i;
 96 
 97     for(i=0;i<length;i++)
 98         if(priTree[i].count!=-2  && priTree[i].count<min  )
 99         {
100             min=priTree[i].count;
101             minpoint=i;
102         }    
103         
104         return minpoint;
105         
106 }
107 
108 /*  构建霍夫曼树  */
109 huffmantable *createHuffmanTree(huffmantable *node, int length)
110 {
111     int i;
112     int m;
113     int Fmin,Smin;
114     int count1;
115     int count2;
116 
117     huffmantable *priArray;
118 
119     //霍夫曼树中节点总数
120     m=2*length-1;
121 
122     //对结构体数组进行扩充
123     priArray=(huffmantable *)malloc(sizeof(huffmantable)*m);
124 
125     //复制读取文件后取得信息到新数组
126     for(i=0;i<length;i++)
127     {
128         //memcpy(&priArray[i],&node[i],sizeof(huffmantable));
129         priArray[i].character=node[i].character;
130         priArray[i].count=node[i].count;
131         priArray[i].lchild=-1;
132         priArray[i].rchild=-1;
133         priArray[i].parent=-1;
134         //priArray
135     }
136 
137     //对非叶子节点进行初始化操作
138     for(i=length;i<m;i++)
139     {
140         priArray[i].count=-1;
141         priArray[i].lchild=-1;
142         priArray[i].rchild=-1;
143         priArray[i].parent=-1;
144     }
145 
146     
147 
148     for(i=0;i<length-1;i++)
149     {
150         //选择第一小频率节点，
151         Fmin=chooseMin(priArray,length+i);
152         count1=priArray[Fmin].count;
153         priArray[Fmin].count=-2;
154         
155         //选择第二小频率节点
156         Smin=chooseMin(priArray,length+i);
157         count2=priArray[Smin].count;
158         priArray[Smin].count=-2;
159         
160         //分别链接到左子节点和右子节点
161         priArray[length+i].lchild=Fmin;
162         priArray[length+i].rchild=Smin;
163         priArray[length+i].count=count1+count2;
164         
165         
166         
167         
168         priArray[Fmin].parent=length+i;
169         priArray[Smin].parent=length+i;
170     }
171 
172     return priArray;
173 
174 }
175 
176 /**
177     对已经构建好了霍夫曼树（以二叉链表形式存储）遍历，生成霍夫曼编码
178 **/
179 huffmancode *huffmancoding(int length,huffmantable *priarray)
180 {
181     huffmancode *coding;
182     char *temp;
183     int i;
184     int clen;
185     int m;
186 
187     coding=(huffmancode *)malloc(sizeof(huffmancode)*length);
188     temp=(char *)malloc(sizeof(char)*length);
189 
190     for(i=0;i<length;i++)
191     {
192         coding[i].character=priarray[i].character;
193     }
194 
195 
196     for(i=0;i<2*length-1;i++)
197     {
198         priarray[i].count=0;
199     }
200 
201     m=2*length-2;
202     
203     clen=0;
204 
205     /* 采用DFS算法进行遍历： 0表示未遍历状态；1表示遍历了左子节点，未遍历右子节点；2 表示遍历了双节点 */
206     while(m!=-1)
207     {
208         if(priarray[m].count==0)
209         {
210             priarray[m].count=1;
211             if(priarray[m].lchild!=-1)
212             {    
213                 
214                 m=priarray[m].lchild;
215                 temp[clen++]='0';
216             }
217             else 
218             {
219                 coding[m].codeString=(char *)malloc(sizeof(char)*clen);
220                 for(i=0;i<clen;i++)
221                 {
222                     coding[m].codeString[i]=temp[i];    
223                 }
224                 coding[m].codeString[clen]='';//表面该叶子节点的字符对应的编码序列结束
225 
226             }
227             
228         }
229         else if( priarray[m].count==1)
230         {
231             priarray[m].count=2;
232             if(priarray[m].rchild!=-1)
233             {
234                 
235                 m=priarray[m].rchild;
236                 temp[clen++]='1';
237             }
238         
239         }
240         else
241         {
242             priarray[m].count=0;
243             m=priarray[m].parent;
244             --clen;
245         }
246 
247     }
248 
249     return coding;
250 }
251 
252 /**
253     使用两个文件操作符，一边读取字符，一边对照霍夫曼编码将对应的编码输入到另一个文件中    
254 **/
255 
256 void zipfunc(huffmancode *code,int length)
257 {
258     FILE *wcpp,*rcpp;
259     errno_t err1,err2;
260     char temp;
261     int i;
262 
263     err1=fopen_s(&wcpp,"zip.txt","w");
264     err2=fopen_s(&rcpp,"test.txt","r");
265 
266     if(err2!=0)
267     {
268         printf("The resourse file can not be found
!");
269     }
270     else
271     {
272         if(err1!=0)
273         {
274             printf("The write file can not be found!
");
275         }
276         else
277         {
278             while((temp=fgetc(rcpp))!=EOF)
279             {
280                 for(i=0;i<length;i++)
281                     if(code[i].character==temp)
282                         break;
283                 fprintf(wcpp,"%s",code[i].codeString);
284             }
285         }
286 
287     }
288     fclose(wcpp);
289     fclose(rcpp);
290 }
291 
292 
293 void unzipfunc(huffmantable *codetable,int length)
294 {
295     FILE *rcpp,*wcpp;
296     errno_t err1,err2;
297     int tempnode;
298     char temp;
299     int i;
300 
301     
302 
303     err1=fopen_s(&rcpp,"zip.txt","r");
304     err2=fopen_s(&wcpp,"unzip.txt","w");
305 
306 
307     if(err1!=0)
308     {
309         printf("The resource file can not be open!
");
310     }
311     else
312     {
313         tempnode=length-1;
314         while((temp=fgetc(rcpp))!=EOF)
315         {
316             //temp=fgetc(rcpp);
317             if(temp=='0')
318             {
319                 tempnode=codetable[tempnode].lchild;
320             }
321             else if(temp=='1')
322             {
323                 tempnode=codetable[tempnode].rchild;
324             }
325             if(codetable[tempnode].lchild==-1 && codetable[tempnode].rchild==-1 )
326             {
327                 fputc(codetable[tempnode].character,wcpp);
328                 tempnode=length-1;
329             }
330             
331 
332         }
333     }
334     fclose(wcpp);
335     fclose(rcpp);
336 
337 }
338 
339 
340 int main()
341 {
342     
343     int i;
344     int length;
345     huffmantable *knode;
346 
347     Length=128;
348 
349     int min;
350 
351     huffmantable *table;
352     huffmancode *result;
353 
354     knode=(huffmantable *)malloc(sizeof(huffmantable)*Length);
355 
356     for(i=0;i<Length;i++)
357     {
358         knode[i].count=0;
359         knode[i].lchild=-1;
360         knode[i].rchild=-1;
361         knode[i].parent=-1;
362     }
363 
364 
365     length=readfile("test.txt",knode);
366     
367     for(i=0;i<length;i++)
368         printf("%c	%d
",knode[i].character,knode[i].count);
369     printf("
");
370 
371 
372     table=createHuffmanTree(knode,length);
373 
374     result=huffmancoding(length,table);
375 
376     zipfunc(result,length);
377     
378     unzipfunc(table,2*length-1);
379 
380     printf("character	huffmancoding
");
381     for(i=0;i<length;i++)
382         printf("%c	%s
",result[i].character,result[i].codeString);
383     printf("
");
384 
385 
386     return 0;
387 }

完整程序代码如下

查看全文

相关阅读:
pg_dump后数据导入报错 -- invalid byte sequence for encoding "UTF8": 0xe5 0xb1
mysql中的read_only和super_read_only
pg_repack安装和使用
 winform 使用Thread.Sleep界面卡死使用 Application.DoEvents 方法防止UI假死
 mysql 使用ifnull 来对应 sql server isnull函数
 计算两个经纬度的距离
 .net framework webapi添加swagger
LINQto实体中不支持指定类型成员“Date”
html5跳转小程序wx-open-launch-weapp踩坑
 vue同时校验两个表单

原文地址：https://www.cnblogs.com/zhengyou/p/3598387.html