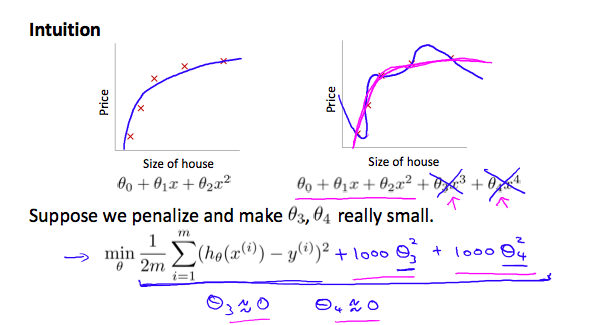
如果我们有过从我们的假设函数,我们可以降低权重,再函数中的增加一些项来增加他们的成本。
比如我们要使下面的函数二次项的权重增大:
![]()
我们要减小θ3x3和θ4x4的影响。实际上,如果不排除这些特性或改变我们假设的形式,我们可以修改我们的成本函数:
![]()
我们已经对最后的θ3和θ4增加了额外的成本。现在,为了使成本函数尽量的接近0,我们将不得不减少θ3和θ4值使他们接近零。
这将大大地减少θ3x3和θ4x4再成本函数中的开销。因此,我们看到,新的假设(由粉红色曲线的描绘)看起来像一个二次函数拟合数据,但是拟合的更好因为额外减少了θ3x3和θ4x4的值。
我们可以把所有θ规范成一个式子:
![]()
λ,是正则化参数。它决定了我们θ参数的成本是多少。
对成本函数使用一个额外的开销总和,我们可以光滑我们的假设函数来降低过拟合。
如果λ的选择太大,可以光滑我们的函数造成欠拟合。
因此,如果λ= 0或太小,会发生什么?