一.数据产生
1 from sklearn.datasets import make_classification, make_blobs 2 from matplotlib.colors import ListedColormap 3 from sklearn.datasets import load_breast_cancer 4 from adspy_shared_utilities import load_crime_dataset 5 6 cmap_bold = ListedColormap(['#FFFF00', '#00FF00', '#0000FF','#000000']) 7 8 #make_regression:随机产生回归模型的数据 9 #参数:n_samples : 数据个数 10 #n_features:数据中变量个数 11 #n_informative:有关变量个数 12 #bias:线性模型中的偏差项 13 #noise:高斯分布的标准差 14 #random_state:随机数的种子生成器 15 16 # 简单(一个参数)的回归数据 17 from sklearn.datasets import make_regression 18 plt.figure() 19 plt.title('Sample regression problem with one input variable') 20 X_R1, y_R1 = make_regression(n_samples = 100, n_features=1, 21 n_informative=1, bias = 150.0, 22 noise = 30, random_state=0) 23 plt.scatter(X_R1, y_R1, marker= 'o', s=50) 24 plt.show() 25 26 27 # 复杂(多参)的回归数据产生 28 from sklearn.datasets import make_friedman1 29 plt.figure() 30 plt.title('Complex regression problem with one input variable') 31 X_F1, y_F1 = make_friedman1(n_samples = 100, 32 n_features = 7, random_state=0) 33 34 plt.scatter(X_F1[:, 2], y_F1, marker= 'o', s=50) 35 plt.show() 36 37 # 分类模型的数据生成 38 plt.figure() 39 plt.title('Sample binary classification problem with two informative features') 40 X_C2, y_C2 = make_classification(n_samples = 100, n_features=2, 41 n_redundant=0, n_informative=2, 42 n_clusters_per_class=1, flip_y = 0.1, 43 class_sep = 0.5, random_state=0) 44 plt.scatter(X_C2[:, 0], X_C2[:, 1], c=y_C2, 45 marker= 'o', s=50, cmap=cmap_bold) 46 plt.show() 47 48 49 # more difficult synthetic dataset for classification (binary) 50 # with classes that are not linearly separable 51 X_D2, y_D2 = make_blobs(n_samples = 100, n_features = 2, centers = 8, 52 cluster_std = 1.3, random_state = 4) 53 y_D2 = y_D2 % 2 54 plt.figure() 55 plt.title('Sample binary classification problem with non-linearly separable classes') 56 plt.scatter(X_D2[:,0], X_D2[:,1], c=y_D2, 57 marker= 'o', s=50, cmap=cmap_bold) 58 plt.show() 59 60 61 # 乳腺癌分类数据集 62 cancer = load_breast_cancer() 63 (X_cancer, y_cancer) = load_breast_cancer(return_X_y = True) 64 65 66 # Communities and Crime dataset 67 (X_crime, y_crime) = load_crime_dataset()




KNN分类
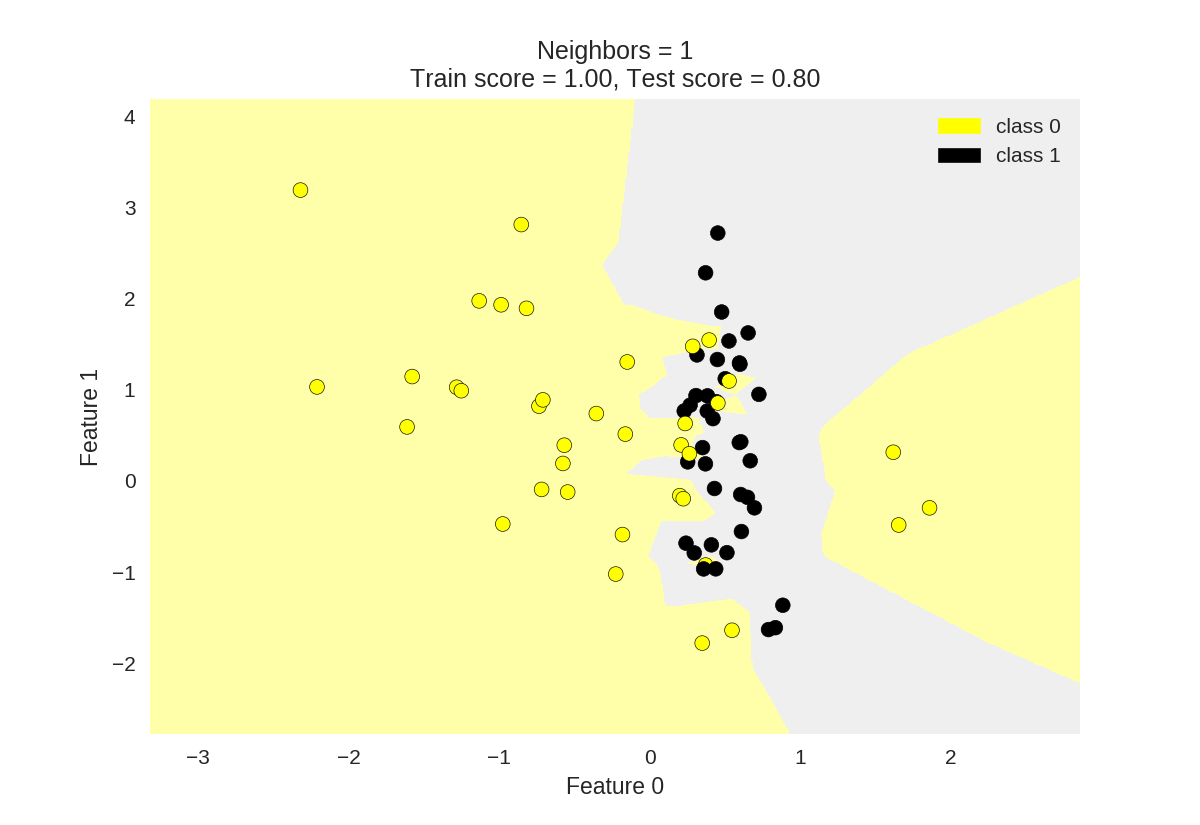
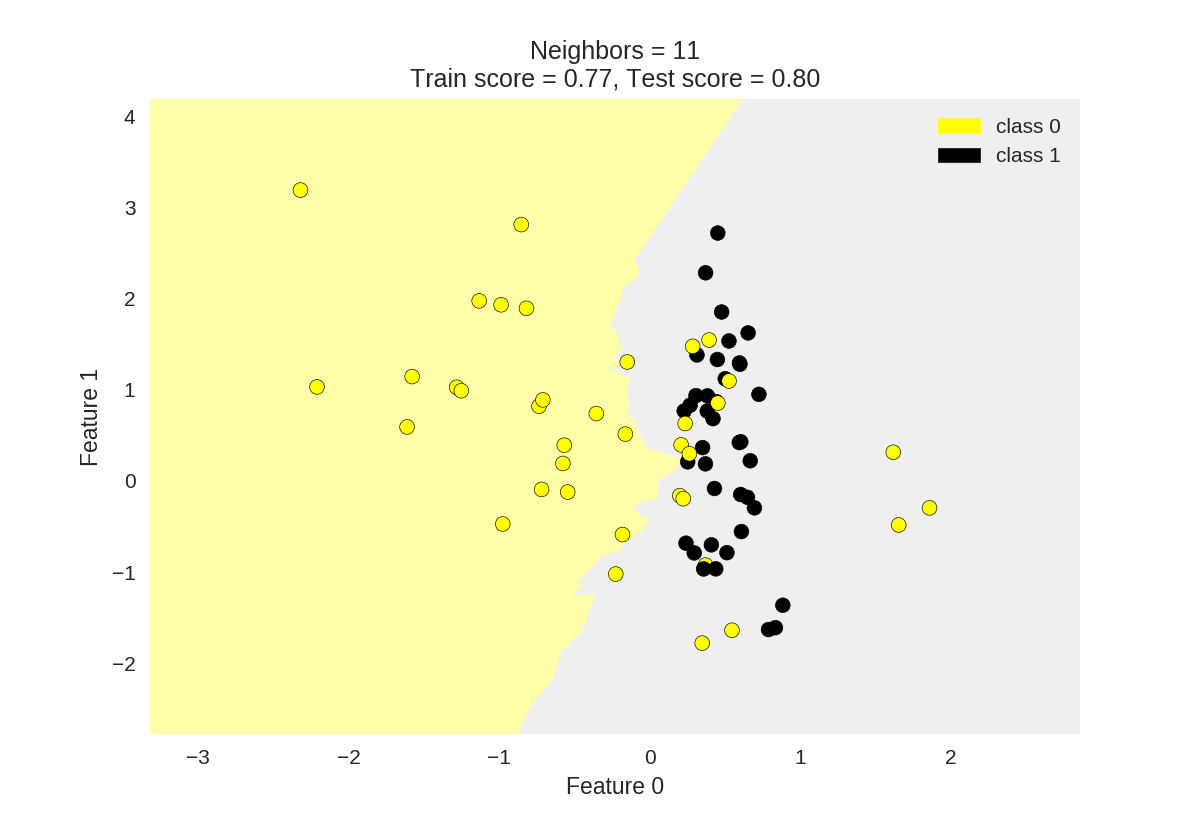
1 from adspy_shared_utilities import plot_two_class_knn 2 3 X_train, X_test, y_train, y_test = train_test_split(X_C2, y_C2, 4 random_state=0) 5 6 #k为knn所选最近邻居个数 7 plot_two_class_knn(X_train, y_train, 1, 'uniform', X_test, y_test) 8 plot_two_class_knn(X_train, y_train, 3, 'uniform', X_test, y_test) 9 plot_two_class_knn(X_train, y_train, 11, 'uniform', X_test, y_test)

KNN回归预测
1 from sklearn.neighbors import KNeighborsRegressor 2 3 X_train, X_test, y_train, y_test = train_test_split(X_R1, y_R1, random_state = 0) 4 5 knnreg = KNeighborsRegressor(n_neighbors = 5).fit(X_train, y_train) 6 7 print(knnreg.predict(X_test)) 8 print('R-squared test score: {:.3f}' 9 .format(knnreg.score(X_test, y_test)))
[ 231.71 148.36 150.59 150.59 72.15 166.51 141.91 235.57 208.26 102.1 191.32 134.5 228.32 148.36 159.17 113.47 144.04 199.23 143.19 166.51 231.71 208.26 128.02 123.14 141.91] R-squared test score: 0.425
#检验k对KNN预测模型结果的影响
1 fig, subaxes = plt.subplots(1, 2, figsize=(8,4)) 2 X_predict_input = np.linspace(-3, 3, 50).reshape(-1,1) 3 X_train, X_test, y_train, y_test = train_test_split(X_R1[0::5], y_R1[0::5], random_state = 0) 4 5 for thisaxis, K in zip(subaxes, [1, 3]): 6 knnreg = KNeighborsRegressor(n_neighbors = K).fit(X_train, y_train) 7 y_predict_output = knnreg.predict(X_predict_input) 8 thisaxis.set_xlim([-2.5, 0.75]) 9 thisaxis.plot(X_predict_input, y_predict_output, '^', markersize = 10, 10 label='Predicted', alpha=0.8) 11 thisaxis.plot(X_train, y_train, 'o', label='True Value', alpha=0.8) 12 thisaxis.set_xlabel('Input feature') 13 thisaxis.set_ylabel('Target value') 14 thisaxis.set_title('KNN regression (K={})'.format(K)) 15 thisaxis.legend() 16 plt.tight_layout()

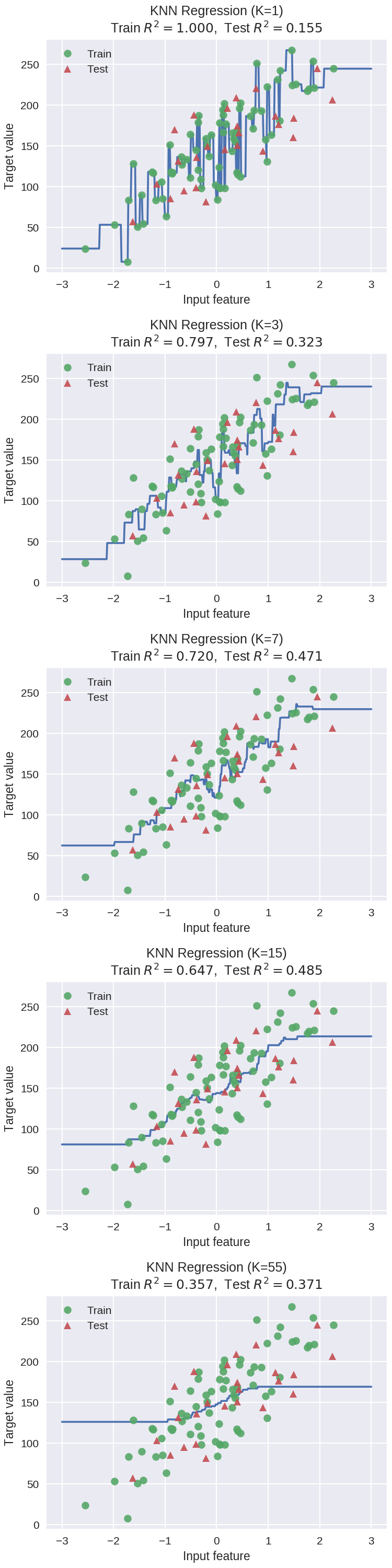
1 # plot k-NN regression on sample dataset for different values of K 2 fig, subaxes = plt.subplots(5, 1, figsize=(5,20))
#生成(-3,3)区间内500个数据 3 X_predict_input = np.linspace(-3, 3, 500).reshape(-1,1) 4 X_train, X_test, y_train, y_test = train_test_split(X_R1, y_R1, 5 random_state = 0) 6 7 for thisaxis, K in zip(subaxes, [1, 3, 7, 15, 55]): 8 knnreg = KNeighborsRegressor(n_neighbors = K).fit(X_train, y_train) 9 y_predict_output = knnreg.predict(X_predict_input) 10 train_score = knnreg.score(X_train, y_train) 11 test_score = knnreg.score(X_test, y_test)
#通过下面这个plot画出线条(其实是离散的点较密形成的) 12 thisaxis.plot(X_predict_input, y_predict_output) 13 thisaxis.plot(X_train, y_train, 'o', alpha=0.9, label='Train') 14 thisaxis.plot(X_test, y_test, '^', alpha=0.9, label='Test') 15 thisaxis.set_xlabel('Input feature') 16 thisaxis.set_ylabel('Target value') 17 thisaxis.set_title('KNN Regression (K={}) 18 Train $R^2 = {:.3f}$, Test $R^2 = {:.3f}$' 19 .format(K, train_score, test_score)) 20 thisaxis.legend() 21 plt.tight_layout(pad=0.4, w_pad=0.5, h_pad=1.0)
KNN参数k对回归预测的影响
线性回归预测模型
1 from sklearn.linear_model import LinearRegression 2 3 X_train, X_test, y_train, y_test = train_test_split(X_R1, y_R1, 4 random_state = 0) 5 linreg = LinearRegression().fit(X_train, y_train) 6 7 #coef_:偏置参数 8 print('linear model coeff (w): {}' 9 .format(linreg.coef_)) 10 #intercept_:各个参数前面的权重 11 #(intercept_[0]*x[0]+...+intercept_[n]*x[n] = y 12 print('linear model intercept (b): {:.3f}' 13 .format(linreg.intercept_)) 14 print('R-squared score (training): {:.3f}' 15 .format(linreg.score(X_train, y_train))) 16 print('R-squared score (test): {:.3f}' 17 .format(linreg.score(X_test, y_test)))
linear model coeff (w): [ 45.71] linear model intercept (b): 148.446 R-squared score (training): 0.679 R-squared score (test): 0.492
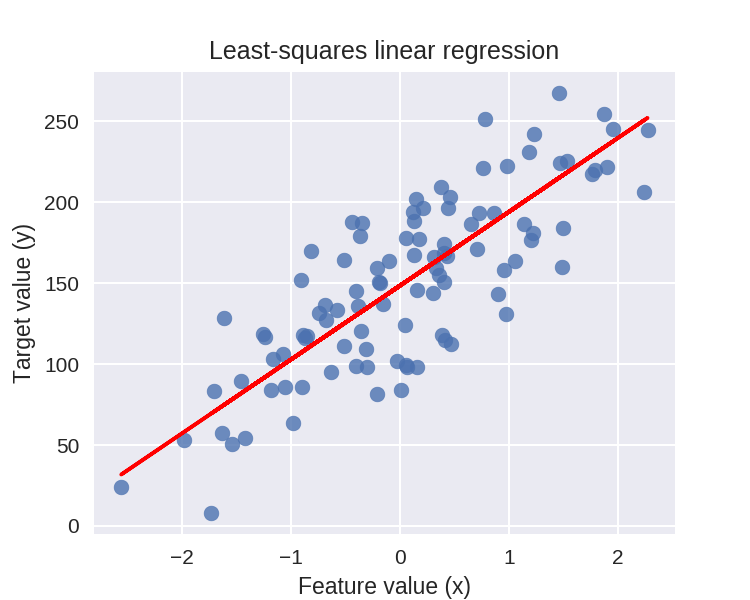
线性回归图示
1 plt.figure(figsize=(5,4)) 2 plt.scatter(X_R1, y_R1, marker= 'o', s=50, alpha=0.8) 3 #画出拟合出来的直线 4 plt.plot(X_R1, linreg.coef_ * X_R1 + linreg.intercept_, 'r-') 5 plt.title('Least-squares linear regression') 6 plt.xlabel('Feature value (x)') 7 plt.ylabel('Target value (y)') 8 plt.show()
多元线性回归预测
1 X_train, X_test, y_train, y_test = train_test_split(X_crime, y_crime, 2 random_state = 0) 3 linreg = LinearRegression().fit(X_train, y_train) 4 5 print('Crime dataset') 6 print('linear model intercept: {}' 7 .format(linreg.intercept_)) 8 print('linear model coeff: {}' 9 .format(linreg.coef_)) 10 print('R-squared score (training): {:.3f}' 11 .format(linreg.score(X_train, y_train))) 12 print('R-squared score (test): {:.3f}' 13 .format(linreg.score(X_test, y_test)))
linear model intercept: 3861.708902399444 linear model coeff: [ 1.62e-03 -1.03e+02 1.61e+01 -2.94e+01 -1.92e+00 -1.47e+01 -2.41e-03 1.46e+00 -1.46e-02 -1.08e+01 4.35e+01 -6.92e+00 4.95e+00 -4.11e+00 -3.63e+00 8.98e-03 8.33e-03 4.84e-03 -5.25e+00 -1.59e+01 7.47e+00 2.31e+00 -2.48e-01 1.22e+01 -2.90e+00 -1.49e+00 4.96e+00 5.21e+00 1.82e+02 1.15e+01 1.54e+02 -3.40e+02 -1.22e+02 2.75e+00 -2.87e+01 2.39e+00 9.44e-01 3.18e+00 -1.17e+01 -5.46e-03 4.24e+01 -1.10e-03 -9.23e-01 5.13e+00 -4.69e+00 1.13e+00 -1.70e+01 -5.00e+01 5.64e+01 -2.94e+01 3.42e-01 -3.10e+01 2.89e+01 -5.46e+01 6.75e+02 8.54e+01 -3.35e+02 -3.17e+01 2.96e+01 7.07e+00 7.46e+01 2.01e-02 -3.96e-01 3.15e+01 1.00e+01 -1.60e+00 -5.63e-01 2.82e+00 -2.96e+01 1.08e+11 -1.01e-03 -1.08e+11 1.08e+11 -3.13e+08 -4.95e-01 3.13e+08 -3.13e+08 1.47e+00 -2.78e+00 1.12e+00 -3.70e+01 1.09e-01 3.07e-01 2.06e+01 9.24e-01 -6.05e-01 -1.92e+00 5.88e-01] R-squared score (training): 0.668 R-squared score (test): 0.520
岭回归
1 from sklearn.linear_model import Ridge 2 X_train, X_test, y_train, y_test = train_test_split(X_crime, y_crime, 3 random_state = 0) 4 #alpha为岭回归的正则化系数 5 linridge = Ridge(alpha=20.0).fit(X_train, y_train) 6 7 print('Crime dataset') 8 print('ridge regression linear model intercept: {}' 9 .format(linridge.intercept_)) 10 print('ridge regression linear model coeff: {}' 11 .format(linridge.coef_)) 12 print('R-squared score (training): {:.3f}' 13 .format(linridge.score(X_train, y_train))) 14 print('R-squared score (test): {:.3f}' 15 .format(linridge.score(X_test, y_test))) 16 print('Number of non-zero features: {}' 17 .format(np.sum(linridge.coef_ != 0)))
Crime dataset ridge regression linear model intercept: -3352.4230358464793 ridge regression linear model coeff: [ 1.95e-03 2.19e+01 9.56e+00 -3.59e+01 6.36e+00 -1.97e+01 -2.81e-03 1.66e+00 -6.61e-03 -6.95e+00 1.72e+01 -5.63e+00 8.84e+00 6.79e-01 -7.34e+00 6.70e-03 9.79e-04 5.01e-03 -4.90e+00 -1.79e+01 9.18e+00 -1.24e+00 1.22e+00 1.03e+01 -3.78e+00 -3.73e+00 4.75e+00 8.43e+00 3.09e+01 1.19e+01 -2.05e+00 -3.82e+01 1.85e+01 1.53e+00 -2.20e+01 2.46e+00 3.29e-01 4.02e+00 -1.13e+01 -4.70e-03 4.27e+01 -1.23e-03 1.41e+00 9.35e-01 -3.00e+00 1.12e+00 -1.82e+01 -1.55e+01 2.42e+01 -1.32e+01 -4.20e-01 -3.60e+01 1.30e+01 -2.81e+01 4.39e+01 3.87e+01 -6.46e+01 -1.64e+01 2.90e+01 4.15e+00 5.34e+01 1.99e-02 -5.47e-01 1.24e+01 1.04e+01 -1.57e+00 3.16e+00 8.78e+00 -2.95e+01 -2.34e-04 3.14e-04 -4.13e-04 -1.80e-04 -5.74e-01 -5.18e-01 -4.21e-01 1.53e-01 1.33e+00 3.85e+00 3.03e+00 -3.78e+01 1.38e-01 3.08e-01 1.57e+01 3.31e-01 3.36e+00 1.61e-01 -2.68e+00] R-squared score (training): 0.671 R-squared score (test): 0.494 Number of non-zero features: 88
岭回归使用归一化变量
1 from sklearn.preprocessing import MinMaxScaler 2 scaler = MinMaxScaler() 3 4 from sklearn.linear_model import Ridge 5 X_train, X_test, y_train, y_test = train_test_split(X_crime, y_crime, 6 random_state = 0) 7 8 #数据归一化 9 X_train_scaled = scaler.fit_transform(X_train) 10 X_test_scaled = scaler.transform(X_test) 11 12 linridge = Ridge(alpha=20.0).fit(X_train_scaled, y_train) 13 14 print('Crime dataset') 15 print('ridge regression linear model intercept: {}' 16 .format(linridge.intercept_)) 17 print('ridge regression linear model coeff: {}' 18 .format(linridge.coef_)) 19 print('R-squared score (training): {:.3f}' 20 .format(linridge.score(X_train_scaled, y_train))) 21 print('R-squared score (test): {:.3f}' 22 .format(linridge.score(X_test_scaled, y_test))) 23 print('Number of non-zero features: {}' 24 .format(np.sum(linridge.coef_ != 0)))
Crime dataset
ridge regression linear model intercept: 933.3906385044113
ridge regression linear model coeff:
[ 88.69 16.49 -50.3 -82.91 -65.9 -2.28 87.74 150.95 18.88
-31.06 -43.14 -189.44 -4.53 107.98 -76.53 2.86 34.95 90.14
52.46 -62.11 115.02 2.67 6.94 -5.67 -101.55 -36.91 -8.71
29.12 171.26 99.37 75.07 123.64 95.24 -330.61 -442.3 -284.5
-258.37 17.66 -101.71 110.65 523.14 24.82 4.87 -30.47 -3.52
50.58 10.85 18.28 44.11 58.34 67.09 -57.94 116.14 53.81
49.02 -7.62 55.14 -52.09 123.39 77.13 45.5 184.91 -91.36
1.08 234.09 10.39 94.72 167.92 -25.14 -1.18 14.6 36.77
53.2 -78.86 -5.9 26.05 115.15 68.74 68.29 16.53 -97.91
205.2 75.97 61.38 -79.83 67.27 95.67 -11.88]
R-squared score (training): 0.615
R-squared score (test): 0.599
Number of non-zero features: 88
正则化参数的岭回归的影响
1 print('Ridge regression: effect of alpha regularization parameter ') 2 #改变alpha(正则化参数) 3 for this_alpha in [0, 1, 10, 20, 50, 100, 1000]: 4 linridge = Ridge(alpha = this_alpha).fit(X_train_scaled, y_train) 5 r2_train = linridge.score(X_train_scaled, y_train) 6 r2_test = linridge.score(X_test_scaled, y_test) 7 num_coeff_bigger = np.sum(abs(linridge.coef_) > 1.0) 8 print('Alpha = {:.2f} num abs(coeff) > 1.0: {}, 9 r-squared training: {:.2f}, r-squared test: {:.2f} ' 10 .format(this_alpha, num_coeff_bigger, r2_train, r2_test))
Ridge regression: effect of alpha regularization parameter Alpha = 0.00 num abs(coeff) > 1.0: 87, r-squared training: 0.67, r-squared test: 0.50 Alpha = 1.00 num abs(coeff) > 1.0: 87, r-squared training: 0.66, r-squared test: 0.56 Alpha = 10.00 num abs(coeff) > 1.0: 87, r-squared training: 0.63, r-squared test: 0.59 Alpha = 20.00 num abs(coeff) > 1.0: 88, r-squared training: 0.61, r-squared test: 0.60 Alpha = 50.00 num abs(coeff) > 1.0: 86, r-squared training: 0.58, r-squared test: 0.58 Alpha = 100.00 num abs(coeff) > 1.0: 87, r-squared training: 0.55, r-squared test: 0.55 Alpha = 1000.00 num abs(coeff) > 1.0: 84, r-squared training: 0.31, r-squared test: 0.30
Lasso 回归
1 from sklearn.linear_model import Lasso 2 from sklearn.preprocessing import MinMaxScaler 3 scaler = MinMaxScaler() 4 5 X_train, X_test, y_train, y_test = train_test_split(X_crime, y_crime, 6 random_state = 0) 7 8 X_train_scaled = scaler.fit_transform(X_train) 9 X_test_scaled = scaler.transform(X_test) 10 11 linlasso = Lasso(alpha=2.0, max_iter = 10000).fit(X_train_scaled, y_train) 12 13 print('Crime dataset') 14 print('lasso regression linear model intercept: {}' 15 .format(linlasso.intercept_)) 16 print('lasso regression linear model coeff: {}' 17 .format(linlasso.coef_)) 18 print('Non-zero features: {}' 19 .format(np.sum(linlasso.coef_ != 0))) 20 print('R-squared score (training): {:.3f}' 21 .format(linlasso.score(X_train_scaled, y_train))) 22 print('R-squared score (test): {:.3f} ' 23 .format(linlasso.score(X_test_scaled, y_test))) 24 print('Features with non-zero weight (sorted by absolute magnitude):') 25 26 for e in sorted (list(zip(list(X_crime), linlasso.coef_)), 27 key = lambda e: -abs(e[1])): 28 if e[1] != 0: 29 print(' {}, {:.3f}'.format(e[0], e[1]))
Crime dataset
lasso regression linear model intercept: 1186.6120619985809
lasso regression linear model coeff:
[ 0. 0. -0. -168.18 -0. -0. 0. 119.69
0. -0. 0. -169.68 -0. 0. -0. 0.
0. 0. -0. -0. 0. -0. 0. 0.
-57.53 -0. -0. 0. 259.33 -0. 0. 0.
0. -0. -1188.74 -0. -0. -0. -231.42 0.
1488.37 0. -0. -0. -0. 0. 0. 0.
0. 0. -0. 0. 20.14 0. 0. 0.
0. 0. 339.04 0. 0. 459.54 -0. 0.
122.69 -0. 91.41 0. -0. 0. 0. 73.14
0. -0. 0. 0. 86.36 0. 0. 0.
-104.57 264.93 0. 23.45 -49.39 0. 5.2 0. ]
Non-zero features: 20
R-squared score (training): 0.631
R-squared score (test): 0.624
Features with non-zero weight (sorted by absolute magnitude):
PctKidsBornNeverMar, 1488.365
PctKids2Par, -1188.740
HousVacant, 459.538
PctPersDenseHous, 339.045
NumInShelters, 264.932
MalePctDivorce, 259.329
PctWorkMom, -231.423
pctWInvInc, -169.676
agePct12t29, -168.183
PctVacantBoarded, 122.692
pctUrban, 119.694
MedOwnCostPctIncNoMtg, -104.571
MedYrHousBuilt, 91.412
RentQrange, 86.356
OwnOccHiQuart, 73.144
PctEmplManu, -57.530
PctBornSameState, -49.394
PctForeignBorn, 23.449
PctLargHouseFam, 20.144
PctSameCity85, 5.198
k(正则化系数)对Lasso回归的影响
1 print('Lasso regression: effect of alpha regularization 2 parameter on number of features kept in final model ') 3 4 for alpha in [0.5, 1, 2, 3, 5, 10, 20, 50]: 5 linlasso = Lasso(alpha, max_iter = 10000).fit(X_train_scaled, y_train) 6 r2_train = linlasso.score(X_train_scaled, y_train) 7 r2_test = linlasso.score(X_test_scaled, y_test) 8 9 print('Alpha = {:.2f} Features kept: {}, r-squared training: {:.2f}, 10 r-squared test: {:.2f} ' 11 .format(alpha, np.sum(linlasso.coef_ != 0), r2_train, r2_test))
Lasso regression: effect of alpha regularization parameter on number of features kept in final model Alpha = 0.50 Features kept: 35, r-squared training: 0.65, r-squared test: 0.58 Alpha = 1.00 Features kept: 25, r-squared training: 0.64, r-squared test: 0.60 Alpha = 2.00 Features kept: 20, r-squared training: 0.63, r-squared test: 0.62 Alpha = 3.00 Features kept: 17, r-squared training: 0.62, r-squared test: 0.63 Alpha = 5.00 Features kept: 12, r-squared training: 0.60, r-squared test: 0.61 Alpha = 10.00 Features kept: 6, r-squared training: 0.57, r-squared test: 0.58 Alpha = 20.00 Features kept: 2, r-squared training: 0.51, r-squared test: 0.50 Alpha = 50.00 Features kept: 1, r-squared training: 0.31, r-squared test: 0.30
多元回归
1 from sklearn.linear_model import LinearRegression 2 from sklearn.linear_model import Ridge 3 from sklearn.preprocessing import PolynomialFeatures 4 5 6 X_train, X_test, y_train, y_test = train_test_split(X_F1, y_F1, 7 random_state = 0) 8 linreg = LinearRegression().fit(X_train, y_train) 9 10 print('linear model coeff (w): {}' 11 .format(linreg.coef_)) 12 print('linear model intercept (b): {:.3f}' 13 .format(linreg.intercept_)) 14 print('R-squared score (training): {:.3f}' 15 .format(linreg.score(X_train, y_train))) 16 print('R-squared score (test): {:.3f}' 17 .format(linreg.score(X_test, y_test))) 18 19 print('对参数开方,使参数变成平方的表示形式') 20 poly = PolynomialFeatures(degree=2) 21 X_F1_poly = poly.fit_transform(X_F1) 22 23 X_train, X_test, y_train, y_test = train_test_split(X_F1_poly, y_F1, 24 random_state = 0) 25 linreg = LinearRegression().fit(X_train, y_train) 26 27 print('(poly deg 2) linear model coeff (w): {}' 28 .format(linreg.coef_)) 29 print('(poly deg 2) linear model intercept (b): {:.3f}' 30 .format(linreg.intercept_)) 31 print('(poly deg 2) R-squared score (training): {:.3f}' 32 .format(linreg.score(X_train, y_train))) 33 print('(poly deg 2) R-squared score (test): {:.3f} ' 34 .format(linreg.score(X_test, y_test))) 35 36 print('使用平方的参数,会很容易导致过拟合,通过对平方参数加上 37 正则化,减少过拟合情况,类似岭回归') 38 39 X_train, X_test, y_train, y_test = train_test_split(X_F1_poly, y_F1, 40 random_state = 0) 41 linreg = Ridge().fit(X_train, y_train) 42 43 print('(poly deg 2 + ridge) linear model coeff (w): {}' 44 .format(linreg.coef_)) 45 print('(poly deg 2 + ridge) linear model intercept (b): {:.3f}' 46 .format(linreg.intercept_)) 47 print('(poly deg 2 + ridge) R-squared score (training): {:.3f}' 48 .format(linreg.score(X_train, y_train))) 49 print('(poly deg 2 + ridge) R-squared score (test): {:.3f}' 50 .format(linreg.score(X_test, y_test)))
linear model coeff (w): [ 4.42 6. 0.53 10.24 6.55 -2.02 -0.32] linear model intercept (b): 1.543 R-squared score (training): 0.722 R-squared score (test): 0.722 对参数开方,使参数变成平方的表示形式 (poly deg 2) linear model coeff (w): [ 3.41e-12 1.66e+01 2.67e+01 -2.21e+01 1.24e+01 6.93e+00 1.05e+00 3.71e+00 -1.34e+01 -5.73e+00 1.62e+00 3.66e+00 5.05e+00 -1.46e+00 1.95e+00 -1.51e+01 4.87e+00 -2.97e+00 -7.78e+00 5.15e+00 -4.65e+00 1.84e+01 -2.22e+00 2.17e+00 -1.28e+00 1.88e+00 1.53e-01 5.62e-01 -8.92e-01 -2.18e+00 1.38e+00 -4.90e+00 -2.24e+00 1.38e+00 -5.52e-01 -1.09e+00] (poly deg 2) linear model intercept (b): -3.206 (poly deg 2) R-squared score (training): 0.969 (poly deg 2) R-squared score (test): 0.805 使用平方的参数,会很容易导致过拟合,通过对平方参数加上 正则化,减少过拟合情况,类似岭回归 (poly deg 2 + ridge) linear model coeff (w): [ 0. 2.23 4.73 -3.15 3.86 1.61 -0.77 -0.15 -1.75 1.6 1.37 2.52 2.72 0.49 -1.94 -1.63 1.51 0.89 0.26 2.05 -1.93 3.62 -0.72 0.63 -3.16 1.29 3.55 1.73 0.94 -0.51 1.7 -1.98 1.81 -0.22 2.88 -0.89] (poly deg 2 + ridge) linear model intercept (b): 5.418 (poly deg 2 + ridge) R-squared score (training): 0.826 (poly deg 2 + ridge) R-squared score (test): 0.825
线性模型用于分类
逻辑回归
使用高度,跨度作为参数进行水果类型分类
1 from sklearn.linear_model import LogisticRegression 2 from adspy_shared_utilities import ( 3 plot_class_regions_for_classifier_subplot) 4 5 fig, subaxes = plt.subplots(1, 1, figsize=(7, 5)) 6 y_fruits_apple = y_fruits_2d == 1 # make into a binary problem: apples vs everything else #as_matrix()把表格转化成矩阵,方便计算
7 X_train, X_test, y_train, y_test = ( 8 train_test_split(X_fruits_2d.as_matrix(), 9 y_fruits_apple.as_matrix(), 10 random_state = 0)) 11 12 clf = LogisticRegression(C=100).fit(X_train, y_train) 13 plot_class_regions_for_classifier_subplot(clf, X_train, y_train, None, 14 None, 'Logistic regression 15 for binary classification Fruit dataset: Apple vs others', 16 subaxes) 17 18 h = 6 19 w = 8 20 print('A fruit with height {} and width {} is predicted to be: {}' 21 .format(h,w, ['not an apple', 'an apple'][clf.predict([[h,w]])[0]])) 22 23 h = 10 24 w = 7 25 print('A fruit with height {} and width {} is predicted to be: {}' 26 .format(h,w, ['not an apple', 'an apple'][clf.predict([[h,w]])[0]])) 27 subaxes.set_xlabel('height') 28 subaxes.set_ylabel('width') 29 30 print('Accuracy of Logistic regression classifier on training set: {:.2f}' 31 .format(clf.score(X_train, y_train))) 32 print('Accuracy of Logistic regression classifier on test set: {:.2f}' 33 .format(clf.score(X_test, y_test)))

A fruit with height 6 and width 8 is predicted to be: an apple A fruit with height 10 and width 7 is predicted to be: not an apple Accuracy of Logistic regression classifier on training set: 0.77 Accuracy of Logistic regression classifier on test set: 0.73
1 from sklearn.linear_model import LogisticRegression 2 from adspy_shared_utilities import ( 3 plot_class_regions_for_classifier_subplot) 4 5 6 X_train, X_test, y_train, y_test = train_test_split(X_C2, y_C2, 7 random_state = 0) 8 9 fig, subaxes = plt.subplots(1, 1, figsize=(7, 5)) 10 clf = LogisticRegression().fit(X_train, y_train) 11 title = 'Logistic regression, simple synthetic dataset C = {:.3f}'.format(1.0) 12 plot_class_regions_for_classifier_subplot(clf, X_train, y_train, 13 None, None, title, subaxes) 14 15 print('Accuracy of Logistic regression classifier on training set: {:.2f}' 16 .format(clf.score(X_train, y_train))) 17 print('Accuracy of Logistic regression classifier on test set: {:.2f}' 18 .format(clf.score(X_test, y_test))) 19
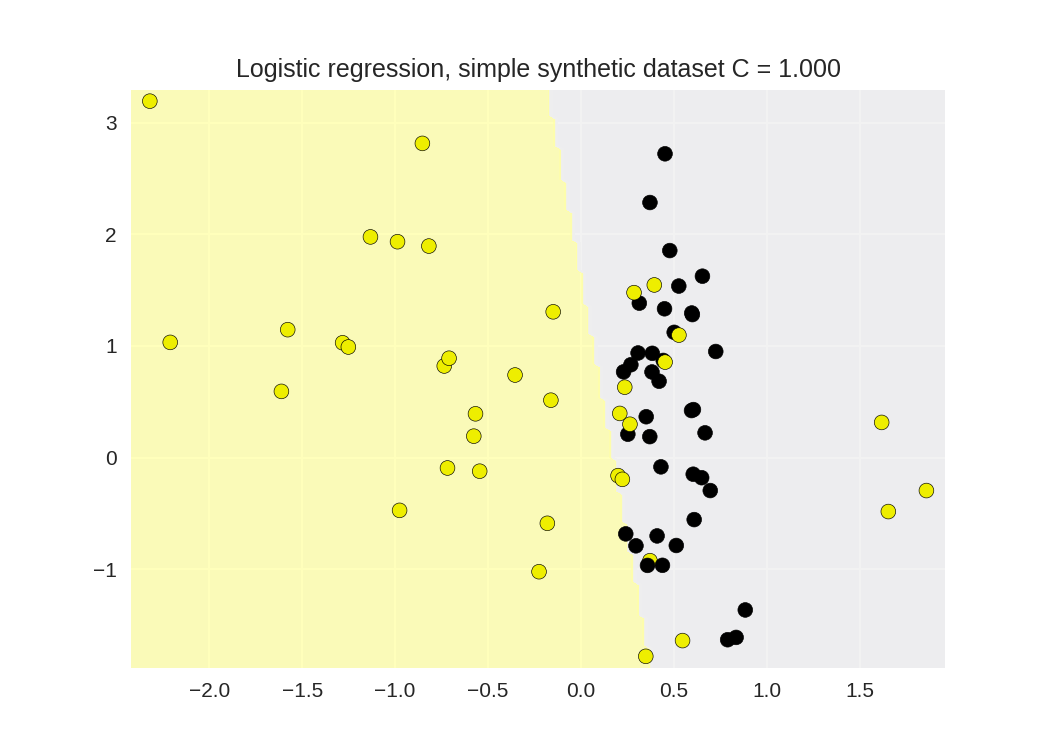
Accuracy of Logistic regression classifier on training set: 0.80 Accuracy of Logistic regression classifier on test set: 0.80
逻辑回归正则化参数的影响
1 X_train, X_test, y_train, y_test = ( 2 train_test_split(X_fruits_2d.as_matrix(), 3 y_fruits_apple.as_matrix(), 4 random_state=0)) 5 6 fig, subaxes = plt.subplots(3, 1, figsize=(4, 10)) 7 8 for this_C, subplot in zip([0.1, 1, 100], subaxes): 9 clf = LogisticRegression(C=this_C).fit(X_train, y_train) 10 title ='Logistic regression (apple vs rest), C = {:.3f}'.format(this_C) 11 12 plot_class_regions_for_classifier_subplot(clf, X_train, y_train, 13 X_test, y_test, title, 14 subplot) 15 plt.tight_layout()
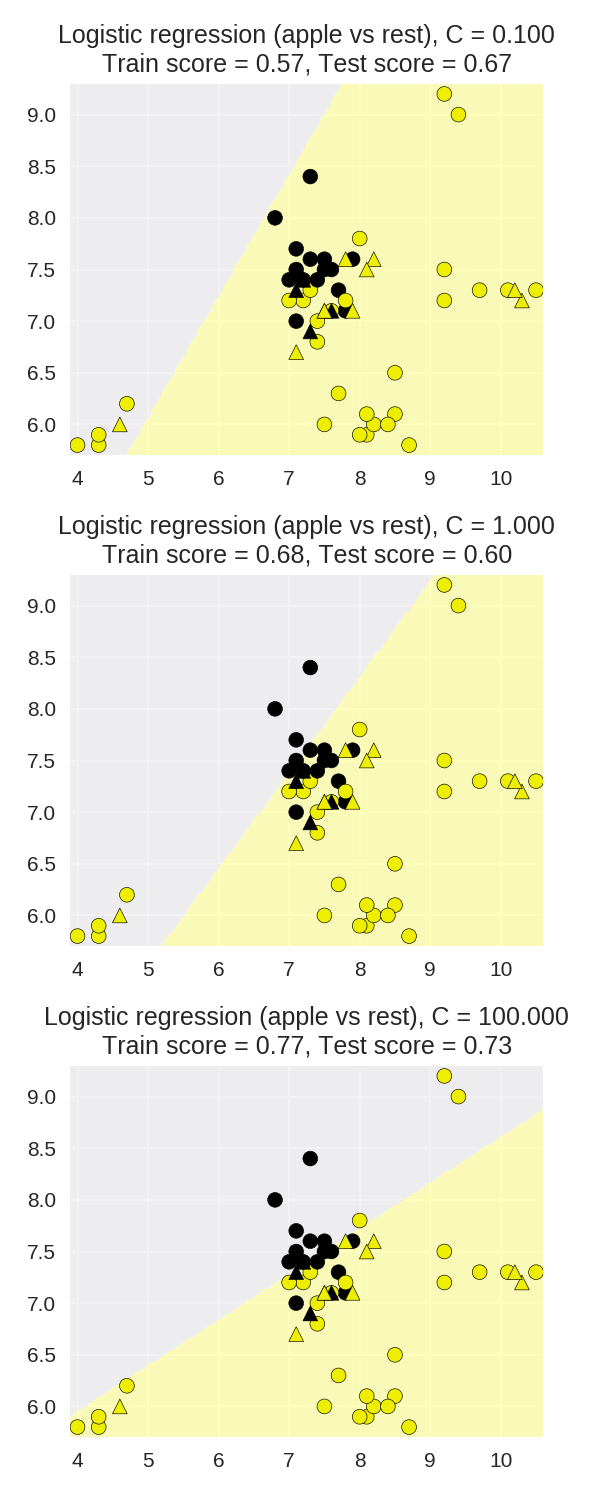
应用于真实数据
1 from sklearn.linear_model import LogisticRegression 2 3 X_train, X_test, y_train, y_test = train_test_split(X_cancer, y_cancer, random_state = 0) 4 5 clf = LogisticRegression().fit(X_train, y_train) 6 print('Breast cancer dataset') 7 print('Accuracy of Logistic regression classifier on training set: {:.2f}' 8 .format(clf.score(X_train, y_train))) 9 print('Accuracy of Logistic regression classifier on test set: {:.2f}' 10 .format(clf.score(X_test, y_test)))
Breast cancer dataset Accuracy of Logistic regression classifier on training set: 0.96 Accuracy of Logistic regression classifier on test set: 0.96
SVM
线性SVM
1 from sklearn.svm import SVC 2 from adspy_shared_utilities import plot_class_regions_for_classifier_subplot 3 4 5 X_train, X_test, y_train, y_test = train_test_split(X_C2, y_C2, random_state = 0) 6 7 fig, subaxes = plt.subplots(1, 1, figsize=(7, 5)) 8 this_C = 1.0 9 #线性核函数 10 clf = SVC(kernel = 'linear', C=this_C).fit(X_train, y_train) 11 title = 'Linear SVC, C = {:.3f}'.format(this_C) 12 plot_class_regions_for_classifier_subplot(clf, X_train, y_train, None, None, title, subaxes)
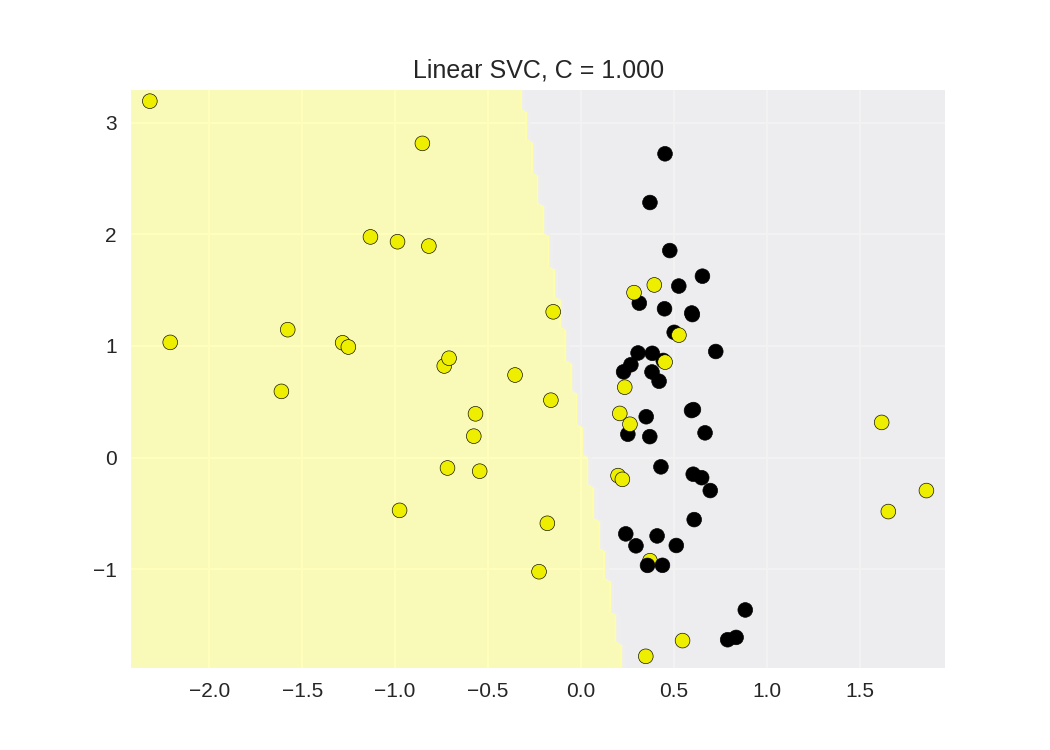
Linear Support Vector Machine: C parameter
1 from sklearn.svm import LinearSVC 2 from adspy_shared_utilities import plot_class_regions_for_classifier 3 4 X_train, X_test, y_train, y_test = train_test_split(X_C2, y_C2, random_state = 0) 5 fig, subaxes = plt.subplots(1, 2, figsize=(8, 4)) 6 7 for this_C, subplot in zip([0.00001, 100], subaxes): 8 clf = LinearSVC(C=this_C).fit(X_train, y_train) 9 title = 'Linear SVC, C = {:.5f}'.format(this_C) 10 plot_class_regions_for_classifier_subplot(clf, X_train, y_train, 11 None, None, title, subplot) 12 plt.tight_layout()
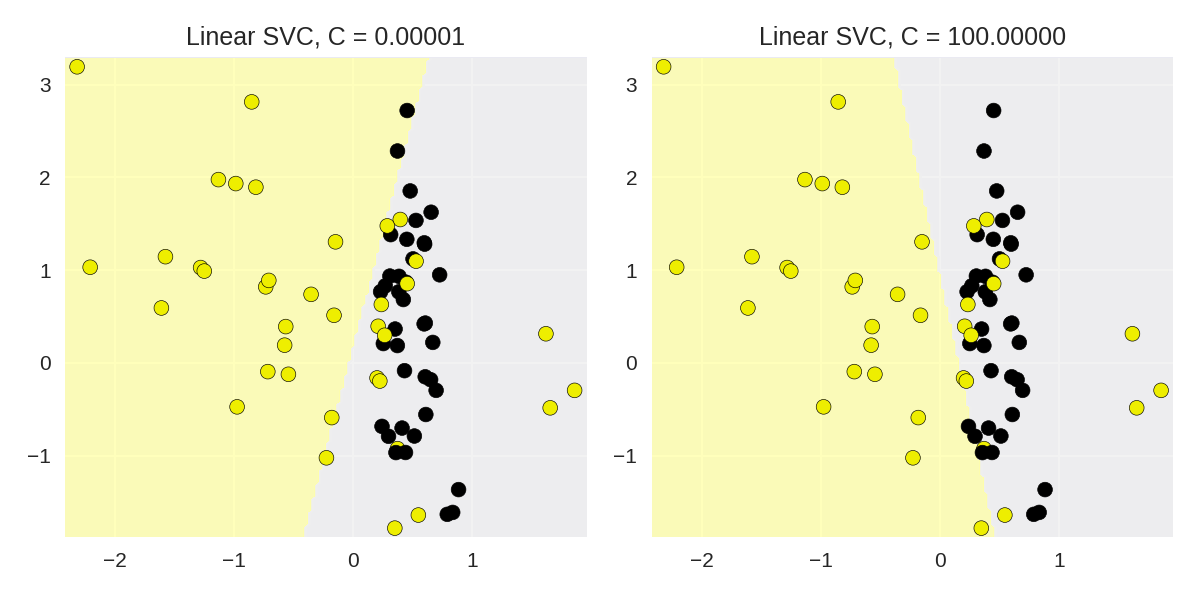
线性SVM使用于真实数据
1 from sklearn.svm import LinearSVC 2 X_train, X_test, y_train, y_test = train_test_split(X_cancer, y_cancer, random_state = 0) 3 4 clf = LinearSVC().fit(X_train, y_train) 5 print('Breast cancer dataset') 6 print('Accuracy of Linear SVC classifier on training set: {:.2f}' 7 .format(clf.score(X_train, y_train))) 8 print('Accuracy of Linear SVC classifier on test set: {:.2f}' 9 .format(clf.score(X_test, y_test)))
Breast cancer dataset Accuracy of Linear SVC classifier on training set: 0.74 Accuracy of Linear SVC classifier on test set: 0.74
使用线性模型进行多分类任务
1 from sklearn.svm import LinearSVC 2 3 X_train, X_test, y_train, y_test = train_test_split(X_fruits_2d, y_fruits_2d, random_state = 0) 4 5 clf = LinearSVC(C=5, random_state = 67).fit(X_train, y_train) 6 print('Coefficients: ', clf.coef_) 7 print('Intercepts: ', clf.intercept_)
Coefficients: [[-0.26 0.71] [-1.63 1.16] [ 0.03 0.29] [ 1.24 -1.64]] Intercepts: [-3.29 1.2 -2.72 1.16]
在水果数据集上使用多分类
1 plt.figure(figsize=(6,6)) 2 colors = ['r', 'g', 'b', 'y'] 3 cmap_fruits = ListedColormap(['#FF0000', '#00FF00', '#0000FF','#FFFF00']) 4 5 plt.scatter(X_fruits_2d[['height']], X_fruits_2d[['width']], 6 c=y_fruits_2d, cmap=cmap_fruits, edgecolor = 'black', alpha=.7) 7 8 x_0_range = np.linspace(-10, 15) 9 10 for w, b, color in zip(clf.coef_, clf.intercept_, ['r', 'g', 'b', 'y']): 11 # Since class prediction with a linear model uses the formula y = w_0 x_0 + w_1 x_1 + b, 12 # and the decision boundary is defined as being all points with y = 0, to plot x_1 as a 13 # function of x_0 we just solve w_0 x_0 + w_1 x_1 + b = 0 for x_1: 14 plt.plot(x_0_range, -(x_0_range * w[0] + b) / w[1], c=color, alpha=.8) 15 16 plt.legend(target_names_fruits) 17 plt.xlabel('height') 18 plt.ylabel('width') 19 plt.xlim(-2, 12) 20 plt.ylim(-2, 15) 21 plt.show()
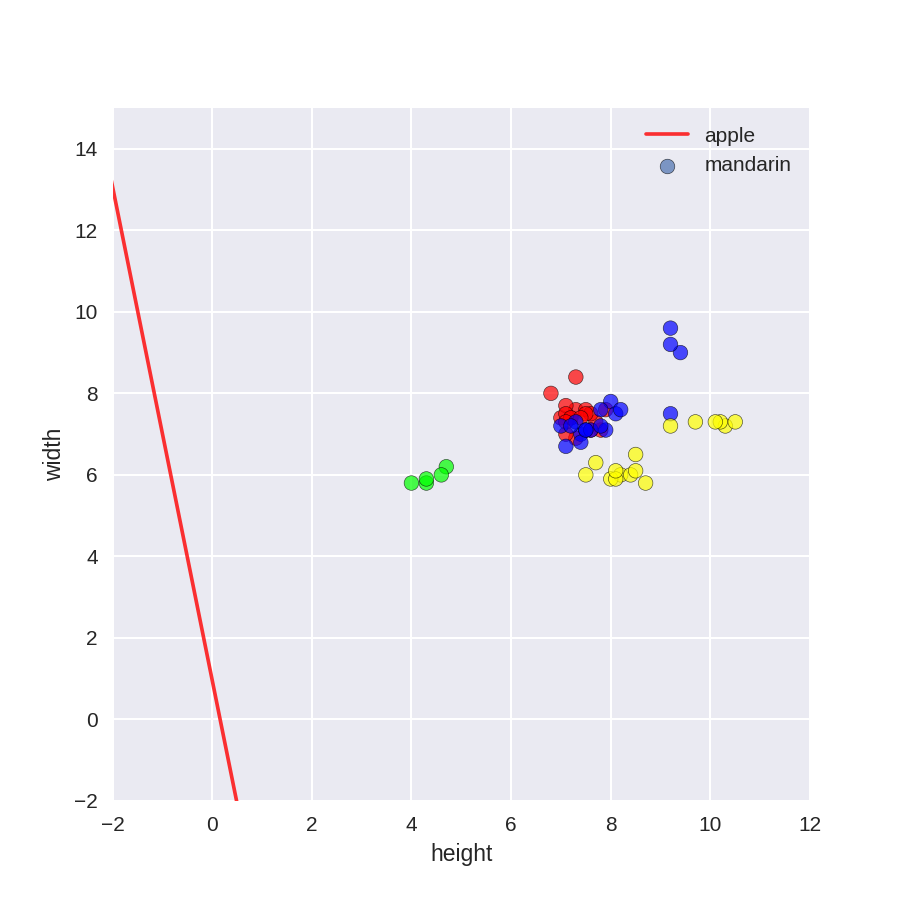
核化SVM
分类模型
1 from sklearn.svm import SVC 2 from adspy_shared_utilities import plot_class_regions_for_classifier 3 4 X_train, X_test, y_train, y_test = train_test_split(X_D2, y_D2, random_state = 0) 5 6 # RBF核函数 7 plot_class_regions_for_classifier(SVC().fit(X_train, y_train), 8 X_train, y_train, None, None, 9 'Support Vector Classifier: RBF kernel') 10 11 # 多项式核函数polynomial kernel, degree = 3 12 plot_class_regions_for_classifier(SVC(kernel = 'poly', degree = 3) 13 .fit(X_train, y_train), X_train, 14 y_train, None, None, 15 'Support Vector Classifier: Polynomial kernel, degree = 3')
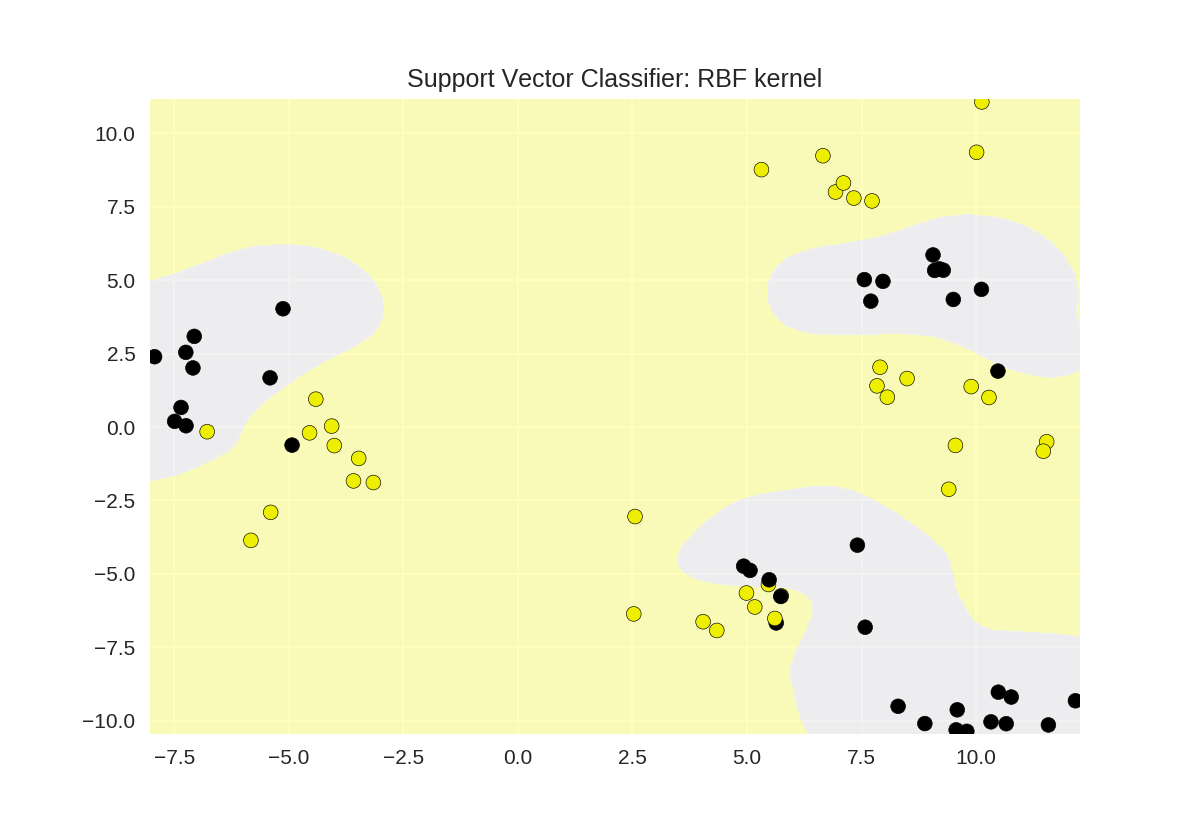

γ参数对RBF核函数SVM的影响
1 from adspy_shared_utilities import plot_class_regions_for_classifier 2 3 X_train, X_test, y_train, y_test = train_test_split(X_D2, y_D2, random_state = 0) 4 fig, subaxes = plt.subplots(3, 1, figsize=(4, 11)) 5 6 for this_gamma, subplot in zip([0.01, 1.0, 10.0], subaxes): 7 clf = SVC(kernel = 'rbf', gamma=this_gamma).fit(X_train, y_train) 8 title = 'Support Vector Classifier: RBF kernel, gamma = {:.2f}'.format(this_gamma) 9 plot_class_regions_for_classifier_subplot(clf, X_train, y_train, 10 None, None, title, subplot) 11 plt.tight_layout()
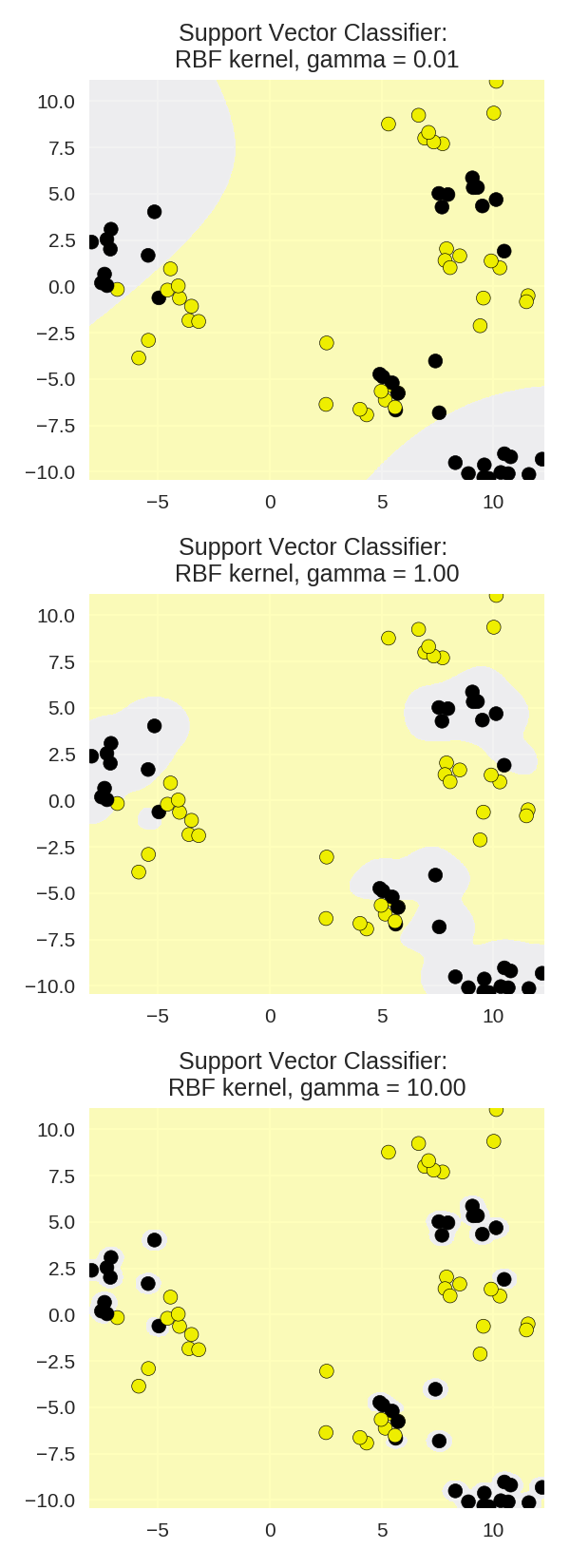
γ和C对RBP核函数SVM的影响
1 from sklearn.svm import SVC 2 from adspy_shared_utilities import plot_class_regions_for_classifier_subplot 3 4 from sklearn.model_selection import train_test_split 5 6 7 X_train, X_test, y_train, y_test = train_test_split(X_D2, y_D2, random_state = 0) 8 fig, subaxes = plt.subplots(3, 4, figsize=(15, 10), dpi=50) 9 10 for this_gamma, this_axis in zip([0.01, 1, 5], subaxes): 11 12 for this_C, subplot in zip([0.1, 1, 15, 250], this_axis): 13 title = 'gamma = {:.2f}, C = {:.2f}'.format(this_gamma, this_C) 14 clf = SVC(kernel = 'rbf', gamma = this_gamma, 15 C = this_C).fit(X_train, y_train) 16 plot_class_regions_for_classifier_subplot(clf, X_train, y_train, 17 X_test, y_test, title, 18 subplot) 19 plt.tight_layout(pad=0.4, w_pad=0.5, h_pad=1.0)

非标准化数据应用于SVM
1 from sklearn.svm import SVC 2 X_train, X_test, y_train, y_test = train_test_split(X_cancer, y_cancer, 3 random_state = 0) 4 5 clf = SVC(C=10).fit(X_train, y_train) 6 print('Breast cancer dataset (unnormalized features)') 7 print('Accuracy of RBF-kernel SVC on training set: {:.2f}' 8 .format(clf.score(X_train, y_train))) 9 print('Accuracy of RBF-kernel SVC on test set: {:.2f}' 10 .format(clf.score(X_test, y_test)))
Breast cancer dataset (unnormalized features) Accuracy of RBF-kernel SVC on training set: 1.00 Accuracy of RBF-kernel SVC on test set: 0.63
SVM应用于标准化数据
1 from sklearn.preprocessing import MinMaxScaler 2 scaler = MinMaxScaler() 3 X_train_scaled = scaler.fit_transform(X_train) 4 X_test_scaled = scaler.transform(X_test) 5 6 clf = SVC(C=10).fit(X_train_scaled, y_train) 7 print('Breast cancer dataset (normalized with MinMax scaling)') 8 print('RBF-kernel SVC (with MinMax scaling) training set accuracy: {:.2f}' 9 .format(clf.score(X_train_scaled, y_train))) 10 print('RBF-kernel SVC (with MinMax scaling) test set accuracy: {:.2f}' 11 .format(clf.score(X_test_scaled, y_test)))
Breast cancer dataset (normalized with MinMax scaling) RBF-kernel SVC (with MinMax scaling) training set accuracy: 0.98 RBF-kernel SVC (with MinMax scaling) test set accuracy: 0.96
交叉验证
1 from sklearn.model_selection import cross_val_score 2 3 clf = KNeighborsClassifier(n_neighbors = 5) 4 X = X_fruits_2d.as_matrix() 5 y = y_fruits_2d.as_matrix() 6 #进行交叉验证 7 cv_scores = cross_val_score(clf, X, y) 8 9 print('Cross-validation scores (3-fold):', cv_scores) 10 print('Mean cross-validation score (3-fold): {:.3f}' 11 .format(np.mean(cv_scores)))
Cross-validation scores (3-fold): [ 0.77 0.74 0.83] Mean cross-validation score (3-fold): 0.781
验证曲线
1 from sklearn.svm import SVC 2 from sklearn.model_selection import validation_curve 3 4 param_range = np.logspace(-3, 3, 4) 5 train_scores, test_scores = validation_curve(SVC(), X, y, 6 param_name='gamma', 7 param_range=param_range, cv=3)
1 print(train_scores)
[[ 0.49 0.42 0.41] [ 0.84 0.72 0.76] [ 0.92 0.9 0.93] [ 1. 1. 0.98]]
1 print(test_scores)
[[ 0.45 0.32 0.33] [ 0.82 0.68 0.61] [ 0.41 0.84 0.67] [ 0.36 0.21 0.39]]
1 # This code based on scikit-learn validation_plot example 2 # See: http://scikit-learn.org/stable/auto_examples/model_selection/plot_validation_curve.html 3 plt.figure() 4 5 train_scores_mean = np.mean(train_scores, axis=1) 6 train_scores_std = np.std(train_scores, axis=1) 7 test_scores_mean = np.mean(test_scores, axis=1) 8 test_scores_std = np.std(test_scores, axis=1) 9 10 plt.title('Validation Curve with SVM') 11 plt.xlabel('$gamma$ (gamma)') 12 plt.ylabel('Score') 13 plt.ylim(0.0, 1.1) 14 lw = 2 15 16 plt.semilogx(param_range, train_scores_mean, label='Training score', 17 color='darkorange', lw=lw) 18 19 plt.fill_between(param_range, train_scores_mean - train_scores_std, 20 train_scores_mean + train_scores_std, alpha=0.2, 21 color='darkorange', lw=lw) 22 23 plt.semilogx(param_range, test_scores_mean, label='Cross-validation score', 24 color='navy', lw=lw) 25 26 plt.fill_between(param_range, test_scores_mean - test_scores_std, 27 test_scores_mean + test_scores_std, alpha=0.2, 28 color='navy', lw=lw) 29 30 plt.legend(loc='best') 31 plt.show()
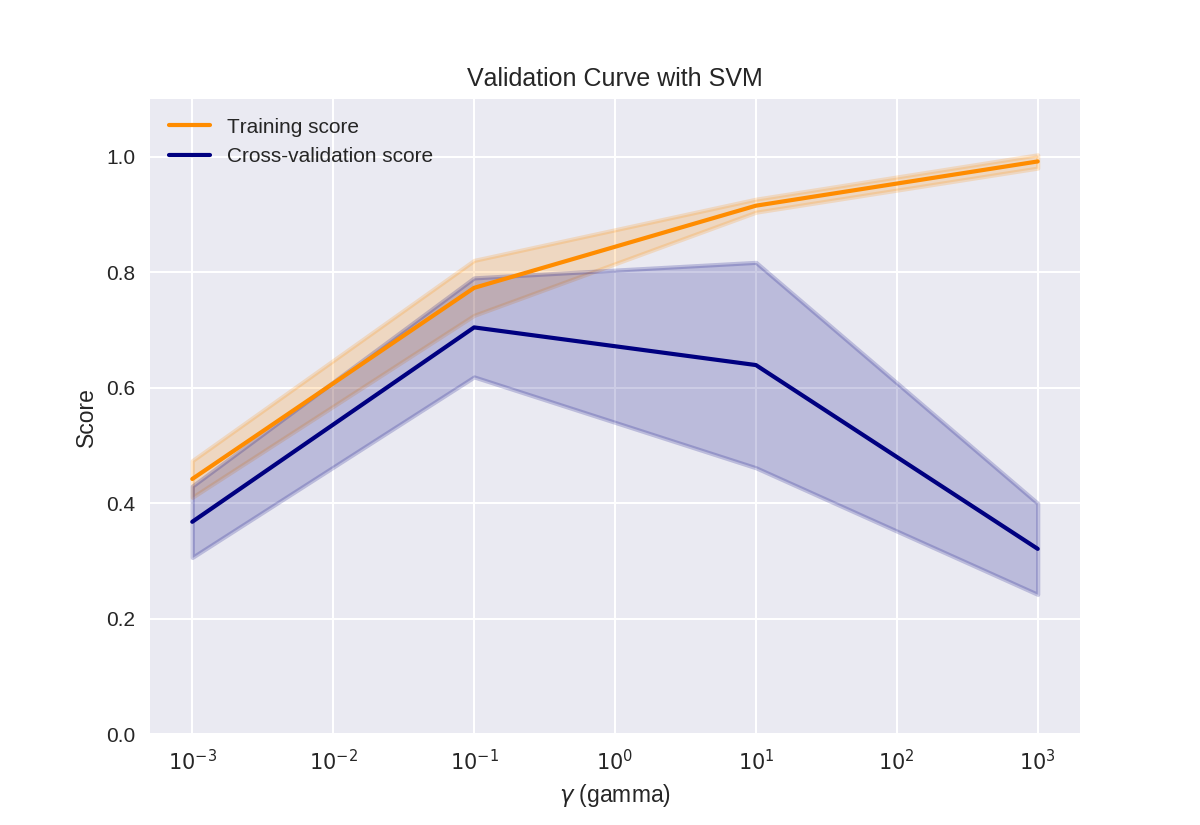
决策树
1 from sklearn.datasets import load_iris 2 from sklearn.tree import DecisionTreeClassifier 3 from adspy_shared_utilities import plot_decision_tree 4 from sklearn.model_selection import train_test_split 5 6 7 iris = load_iris() 8 9 X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state = 3) 10 clf = DecisionTreeClassifier().fit(X_train, y_train) 11 12 print('Accuracy of Decision Tree classifier on training set: {:.2f}' 13 .format(clf.score(X_train, y_train))) 14 print('Accuracy of Decision Tree classifier on test set: {:.2f}' 15 .format(clf.score(X_test, y_test)))
设置树的深度避免过拟合
#max_depth设置决策树的最大深度
1 clf2 = DecisionTreeClassifier(max_depth = 3).fit(X_train, y_train) 2 3 print('Accuracy of Decision Tree classifier on training set: {:.2f}' 4 .format(clf2.score(X_train, y_train))) 5 print('Accuracy of Decision Tree classifier on test set: {:.2f}' 6 .format(clf2.score(X_test, y_test)))
Accuracy of Decision Tree classifier on training set: 0.98 Accuracy of Decision Tree classifier on test set: 0.97
可视化决策树
1 plot_decision_tree(clf, iris.feature_names, iris.target_names)
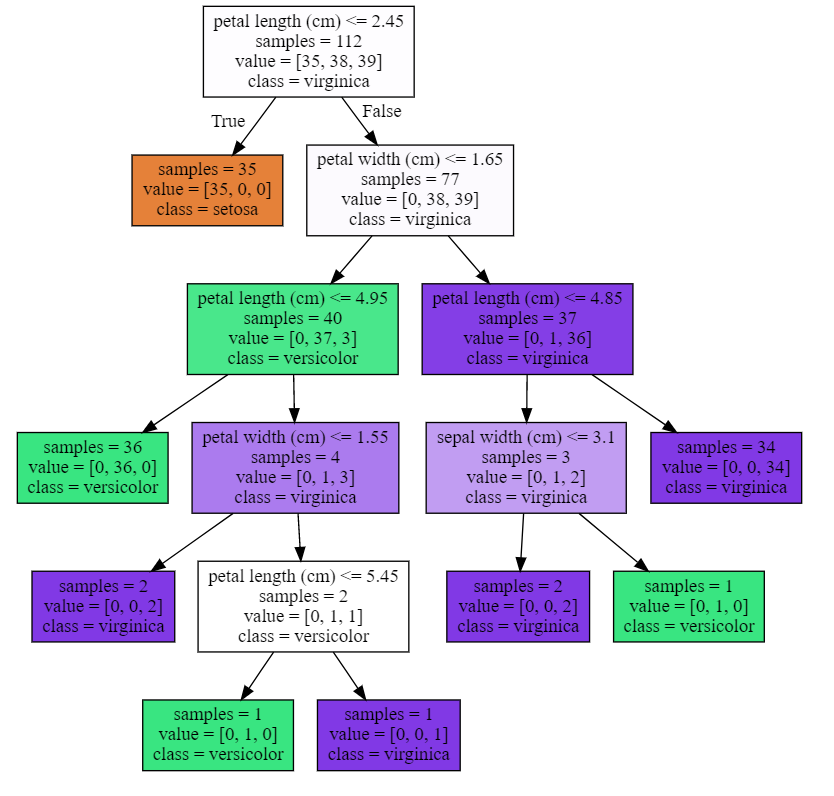
1 #决策树的最大深度为3 2 plot_decision_tree(clf2, iris.feature_names, iris.target_names)

变量的重要性
1 from adspy_shared_utilities import plot_feature_importances 2 3 plt.figure(figsize=(10,4), dpi=80) 4 plot_feature_importances(clf, iris.feature_names) 5 plt.show() 6 7 print('Feature importances: {}'.format(clf.feature_importances_))
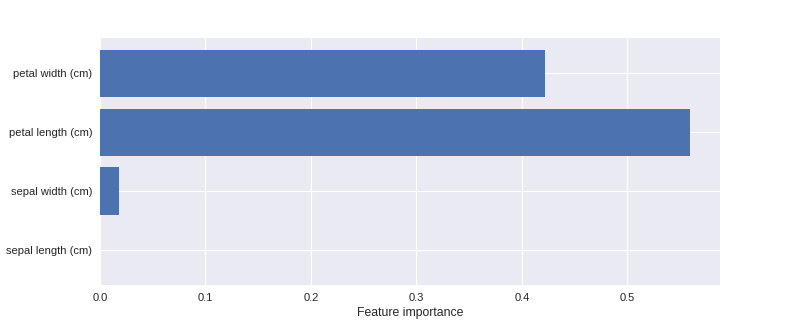
Feature importances: [ 0. 0.02 0.56 0.42]
1 from sklearn.tree import DecisionTreeClassifier 2 from adspy_shared_utilities import plot_class_regions_for_classifier_subplot 3 4 X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state = 0) 5 fig, subaxes = plt.subplots(6, 1, figsize=(6, 32)) 6 7 pair_list = [[0,1], [0,2], [0,3], [1,2], [1,3], [2,3]] 8 tree_max_depth = 4 9 10 for pair, axis in zip(pair_list, subaxes): 11 X = X_train[:, pair] 12 y = y_train 13 14 clf = DecisionTreeClassifier(max_depth=tree_max_depth).fit(X, y) 15 title = 'Decision Tree, max_depth = {:d}'.format(tree_max_depth) 16 plot_class_regions_for_classifier_subplot(clf, X, y, None, 17 None, title, axis, 18 iris.target_names) 19 20 axis.set_xlabel(iris.feature_names[pair[0]]) 21 axis.set_ylabel(iris.feature_names[pair[1]]) 22 23 plt.tight_layout() 24 plt.show()

决策树应用于真实数据
1 from sklearn.tree import DecisionTreeClassifier 2 from adspy_shared_utilities import plot_decision_tree 3 from adspy_shared_utilities import plot_feature_importances 4 5 X_train, X_test, y_train, y_test = train_test_split(X_cancer, y_cancer, random_state = 0) 6 7 clf = DecisionTreeClassifier(max_depth = 4, min_samples_leaf = 8, 8 random_state = 0).fit(X_train, y_train) 9 10 plot_decision_tree(clf, cancer.feature_names, cancer.target_names)

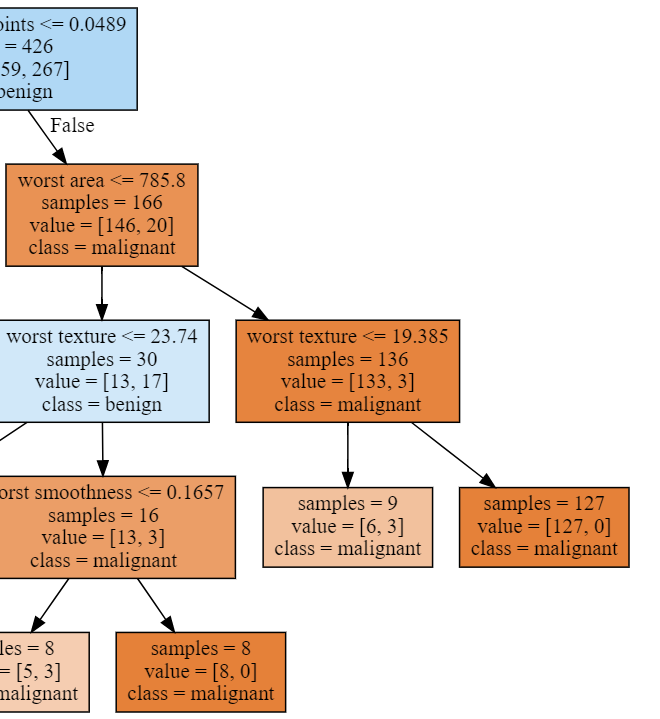
1 print('Breast cancer dataset: decision tree') 2 print('Accuracy of DT classifier on training set: {:.2f}' 3 .format(clf.score(X_train, y_train))) 4 print('Accuracy of DT classifier on test set: {:.2f}' 5 .format(clf.score(X_test, y_test))) 6 7 plt.figure(figsize=(10,6),dpi=80) 8 plot_feature_importances(clf, cancer.feature_names) 9 plt.tight_layout() 10 11 plt.show()
Breast cancer dataset: decision tree Accuracy of DT classifier on training set: 0.96 Accuracy of DT classifier on test set: 0.94
