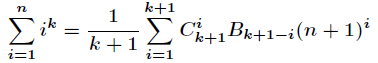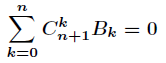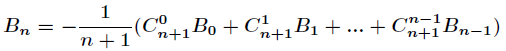求自然数幂和,就是一条公式,然后用代码实现;
公式描述如下:
可以看出只要我们预处理出每一项,就可以在线性时间内求得自然数的幂和。前面的倒数可以用递推法求逆元
预处理,组合数也可以预处理,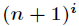
伯努利数满足条件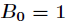
那么继续得到
这就是伯努利数的递推式,逆元部分同样可以预处理。
代码:
typedef long long ll;
typedef unsigned long long ull;
const ll N=2005;
const ll mod=1e9+7;
ll inv[N],B[N];
ll C[N][N];
ll tmp[N];
ll n,k;
void init()
{
//预处理组合数
for(int i=0;i<N;i++)
{
C[i][0]=1;
for(int j=1;j<=i;j++)
C[i][j]=(C[i-1][j]%mod+C[i-1][j-1]%mod)%mod;
}
//预处理逆元
inv[1]=1;
for(int i=2;i<N;i++)
inv[i]=(mod-mod/i)*inv[mod%i]%mod;
;
// 预处理伯努利数
B[0]=1;
for(int i=1;i<N;i++)
{
ll ans=0;
if(i==N-1)break;
for(int j=0;j<i;j++)
{
ans+=C[i+1][j]*B[j];
ans%=mod;
}
ans*=-inv[i+1];
ans=(ans%mod+mod)%mod;
B[i]=ans;
}
}
ll work(ll k)
{
ll ans=inv[k+1];
ll sum=0;
for(int i=1;i<=k+1;i++)
{
sum+=C[k+1][i]*tmp[i]%mod*B[k+1-i]%mod;
sum%=mod;
}
ans*=sum;
ans%=mod;
return ans;
}
ll sum(ll n,ll k)
{
if(n<0)return 0;
n%=mod;
tmp[0]=1;
for(int i=1;i<N;i++)
tmp[i]=tmp[i-1]*(n+1)%mod;
return work(k);
}
参考博客:https://blog.csdn.net/acdreamers/article/details/38929067