和为S的两个数字
题目一:输入一个递增排序的数组和一个数字s,在数组中查找两个数,使得他们的和正好是S,如果有多对数字的和等于s,输出任意一对即可。
解题思路:首先想到的方法是O(n^2)的方法,也就是先在数组中固定一个数字,再一次判断数组中其余的n-1个数字与它的和是不是等于s,面试官会告诉我们这不是最好的办法。不过没关系,至少面试官知道我们的思维还是比较敏捷的。
快速解答方式:
我们以数组{1、2、4、7、11、15}及期待的和15为例详细分析一下这个过程。首先定义两个指针,第一个指针指向数组的第一个(也是最小的)数字1,第二个指针指向数组的最后一个(也是最大的)数字15.这两个数字的和16大于15,因此我们把第二个指针向前移动一个数字,让它指向11.这个时候两个数字1与11的和是12,雄安与15.接下来我们把第一个指针向后移动一个数字指向2.此时两个数字2与11的和13,还是小于15.我们再一次向后移动第一个指针,让他指向数字4.数字4、11的和是15,正是我们期待的结果。过程如下表所示:
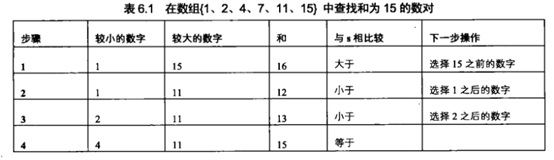
题目二:输入一个整数s,打印出所有和为s的连续正数序列(至少含有两个数)。例如输入15,由于1+2+3+4+5=4+5+6=7+8=15,所以结果打印出3个连续序列1-5,4-6和7-8.
解题思路:以求和为9的所有连续序列为例,我们先把small初始化为1,big初始化为2.此时介于small和big之间的序列是{1,2},序列的和为3,小于9,所以我们下一步要让序列包含更多的数字。我们把big增加1变成3.此时序列为{1,2,3}.由于序列的和是6,仍然小于9,我们接下来再增加big变成4,介于small和big之间的序列也随之变成{1,2,3,4}.由于序列的和10大于9,我们要删去去序列中的一些数字,于是我们增加small变成2,此时得到的序列是{2,3,4},序列的和正好是9.我们找到了第一个和为9的连续序列,把它打印出来。接下来我们再增加big,重复前面的过程,可以找到第二个和为9的连续序列{4,5},可以用下表总结过程:
