线性回归
回归是一种极易理解的模型,就相当于y=f(x),表明自变量 x 和因变量 y 的关系。最常见问题有如 医生治病时的望、闻、问、切之后判定病人是否生了什么病,其中的望闻问切就是获得自变量x,即特征数据,判断是否生病就相当于获取因变量y,即预测分类。
最简单的回归是线性回归,如图1.a所示,X为数据点——肿瘤的大小,Y为观测值——是否是恶性肿瘤。通过构建线性回归模型,如 hθ (x) 所示,构建线性回归模型后,可以根据肿瘤大小,预测是否为恶性肿瘤。h θ (x)≥.05为恶性,h θ (x)<0.5为良性:

然而线性回归的鲁棒性很差,例如在图1.b的数据集上建立回归,因最右边噪点的存在,使回归模型在训练集上表现都很差。这主要是由于线性回归在整个实数域内敏感度一致,而分类范围,需要在[0,1]。
线性回归的应用场合大多是回归分析,一般不用在分类问题上,原因可以概括为一下两个:
1)回归模型是连续模型,即预测出的值都是连续值(实数值),非离散值;
2)预测结果受样本噪声的影响比较大。
逻辑回归
逻辑回归就是一种减小预测范围,将预测值限定为[0,1]间的一种回归模型,其回归方程与回归曲线如图2所示。逻辑曲线在z=0时,十分敏感,在z>>0或z<<0处,都不敏感,将预测值限定为(0,1)。
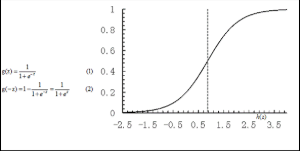
图2 逻辑方程与逻辑曲线
逻辑回归其实仅为在线性回归的基础上,套用了一个逻辑函数,
线性函数的值越接近于正无穷大,概率值就越近1;反之,其值越接近于负无穷,概率值就越接近于0,这样的模型就是LR模型。
LR本质上还是线性回归,只是特征到结果的映射过程中加了一层函数映射,即sigmoid函数,即先把特征线性求和,然后使用sigmoid函数将线性和约束至(0,1)之间,结果值用于二分或回归预测。
Logistic回归虽然名字里带“回归”,但是它实际上是一种分类方法,主要用于两分类问题(即输出只有两种,分别代表两个类别),但也就由于这个逻辑函数,逻辑回归成为了机器学习领域一颗耀眼的明星,更是计算广告学的核心。对于多元逻辑回归,可用如下公式似合分类,其中公式(4)的变换,将在逻辑回归模型参数估计时,化简公式带来很多益处,y={0,1}为分类结果

对于训练数据集,特征数据x={x 1 , x 2 , … , x m }和对应的分类数据y={y 1 , y 2 , … , y m }。构建逻辑回归模型f(θ),最典型的构建方法便是应用极大似然估计。首先,对于单个样本,其后验概率为:
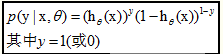
那么,极大似然函数为(后验概率的连乘):

log似然是:
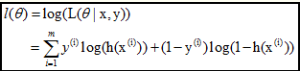
2、梯度下降法
由第1节可知,求逻辑回归模型l(θ),等价于:

采用梯度下降法:

从而迭代θ至收敛即可:

3 模型评估
对于LR分类模型的评估,常用AUC来评估
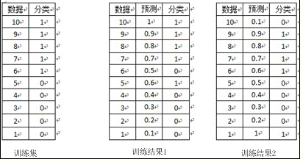
对于训练集的分类,训练方法1和训练方法2分类正确率都为80%,但明显可以感觉到训练方法1要比训练方法2好。因为训练方法1中,5和6两数据分类错误,但这两个数据位于分类面附近,而训练方法2中,将10和1两个数据分类错误,但这两个数据均离分类面较远。
AUC正是衡量分类正确度的方法,将训练集中的label看两类{0,1}的分类问题,分类目标是将预测结果尽量将两者分开。将每个0和1看成一个pair关系,团中的训练集共有5*5=25个pair关系,只有将所有pair关系一至时,分类结果才是最好的,而auc为1。在训练方法1中,与10相关的pair关系完全正确,同样9、8、7的pair关系也完全正确,但对于6,其pair关系(6,5)关系错误,而与4、3、2、1的关系正确,故其auc为(25-1)/25=0.96;对于分类方法2,其6、7、8、9的pair关系,均有一个错误,即(6,1)、(7,1)、(8,1)、(9,1),对于数据点10,其正任何数据点的pair关系,都错误,即(10,1)、(10,2)、(10,3)、(10,4)、(10,5),故方法2的auc为(25-4-5)/25=0.64,因而正如直观所见,分类方法1要优于分类方法2。
回归问题的条件/前提:
1) 收集的数据
2) 假设的模型,即一个函数,这个函数里含有未知的参数,通过学习,可以估计出参数。然后利用这个模型去预测/分类新的数据。
常见的问题:
1、线性回归求未知参数的方法?
假设 特征 和 结果 都满足线性。即不大于一次方。这个是针对 收集的数据而言。
收集的数据中,每一个分量,就可以看做一个特征数据。每个特征至少对应一个未知的参数。这样就形成了一个线性模型函数,向量表示形式:
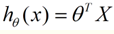
这个就是一个组合问题,已知一些数据,如何求里面的未知参数,给出一个最优解。 一个线性矩阵方程,直接求解,很可能无法直接求解。有唯一解的数据集,微乎其微。
基本上都是解不存在的超定方程组。因此,需要退一步,将参数求解问题,转化为求最小误差问题,求出一个最接近的解,这就是一个松弛求解。
求一个最接近解,直观上,就能想到,误差最小的表达形式。仍然是一个含未知参数的线性模型,一堆观测数据,其模型与数据的误差最小的形式,模型与数据差的平方和最小:
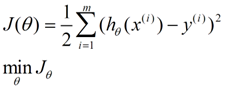
这就是损失函数的来源。接下来,就是求解这个函数的方法,有最小二乘法,梯度下降法。
最小二乘法
是一个直接的数学求解公式,不过它要求X是列满秩的,

梯度下降法
分别有梯度下降法,批梯度下降法,增量梯度下降。本质上,都是偏导数,步长/最佳学习率,更新,收敛的问题。这个算法只是最优化原理中的一个普通的方法,可以结合最优化原理来学,就容易理解了。
2、逻辑回归和线性回归的联系、异同?
逻辑回归的模型 是一个非线性模型,sigmoid函数,又称逻辑回归函数。但是它本质上又是一个线性回归模型,因为除去sigmoid映射函数关系,其他的步骤,算法都是线性回归的。可以说,逻辑回归,都是以线性回归为理论支持的。
只不过,线性模型,无法做到sigmoid的非线性形式,sigmoid可以轻松处理0/1分类问题。
另外它的推导含义:仍然与线性回归的最大似然估计推导相同,最大似然函数连续积(这里的分布,可以使伯努利分布,或泊松分布等其他分布形式),求导,得损失函数。
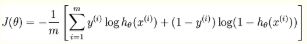
逻辑回归函数
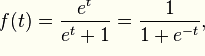
表现了0,1分类的形式
损失函数:损失函数越小,模型就越好,而且损失函数 尽量 是一个凸函数,便于收敛计算。
线性回归,采用的是平方损失函数。而逻辑回归采用的是 对数 损失函数。
应用举例:
是否垃圾邮件分类?
是否肿瘤、癌症诊断?
是否金融欺诈?
3、过拟合问题问题起源?如何解决?
模型太复杂,参数过多,特征数目过多。
方法: 1) 减少特征的数量,有人工选择,或者采用模型选择算法
2) 正则化,即保留所有特征,但降低参数的值的影响。正则化的优点是,特征很多时,每个特征都会有一个合适的影响因子。
为防止过度拟合的模型出现(过于复杂的模型),在损失函数里增加一个每个特征的惩罚因子。这个就是正则化。如正则化的线性回归 的 损失函数
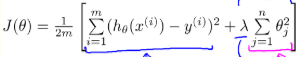
lambda就是惩罚因子;
正则化是模型处理的典型方法。也是结构风险最小的策略。在经验风险(误差平方和)的基础上,增加一个惩罚项/正则化项
从贝叶斯估计来看,正则化项对应模型的先验概率,复杂模型有较大先验概率,简单模型具有较小先验概率。
4、概率解释:线性回归中为什么选用平方和作为误差函数?
假设模型结果与测量值 误差满足,均值为0的高斯分布,即正态分布。这个假设是靠谱的,符合一般客观统计规律。
数据x与y的条件概率
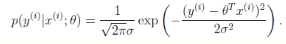
若使 模型与测量数据最接近,那么其概率积就最大。概率积,就是概率密度函数的连续积,这样,就形成了一个最大似然函数估计。对最大似然函数估计进行推导,就得出了求导后结果: 平方和最小公式
5、经验风险、期望风险、经验损失、结构风险之间的区别与联系?
期望风险(真实风险),可理解为 模型函数固定时,数据 平均的 损失程度,或“平均”犯错误的程度。 期望风险是依赖损失函数和概率分布的。只有样本,是无法计算期望风险的
所以,采用经验风险,对期望风险进行估计,并设计学习算法,使其最小化。即经验风险最小化(Empirical Risk Minimization)ERM,而经验风险是用损失函数来评估的、计算的。对于分类问题,经验风险,就训练样本错误率。对于函数逼近,拟合问题,经验风险就是平方训练误差。对于概率密度估计问题,ERM,就是最大似然估计法。
而经验风险最小,并不一定就是期望风险最小,无理论依据。只有样本无限大时,经验风险就逼近了期望风险。如何解决这个问题? 统计学习理论SLT,支持向量机SVM就是专门解决这个问题的。有限样本条件下,学习出一个较好的模型。由于有限样本下,经验风险Remp[f]无法近似期望风险R[f] 。因此,统计学习理论给出了二者之间的关系:R[f] <= ( Remp[f] + e )
而右端的表达形式就是结构风险,是期望风险的上界。而e = g(h/n)是置信区间,是VC维h的增函数,也是样本数n的减函数。VC维的定义在 SVM,SLT中有详细介绍。e依赖h和n,若使期望风险最小,只需关心其上界最小,即e最小化。所以,需要选择合适的h(核函数)和n(样本数)。这就是结构风险最小化Structure Risk Minimization,SRM. SVM就是SRM的近似实现,SVM中的概念另有一大筐。就此打住。
6、核函数的物理意义?
映射到高维,使其变得线性可分。什么是高维?如一个一维数据特征x,转换为(x,x^2, x^3),就成为了一个三维特征,且线性无关。一个一维特征线性不可分的特征,在高维,就可能线性可分了。
Regression问题的常规步骤为:
- 寻找h函数(即hypothesis);
- 构造J函数(损失函数);
- 想办法使得J函数最小并求得回归参数(θ)
7、LR的优缺点
优点:
1)预测结果是介于0和1之间的概率
2)可以适用于连续性和类别性自变量
3)容易使用和解释
缺点:
1)对模型中自变量多重共线性较为敏感,例如两个高度相关自变量同时放入模型,可能导致较弱的一个自变量回归符号不符合预期,符号被扭转。需要利用因子分析或者变量聚类分析等手段来选择代表性的自变量,以减少候选变量之间的相关性;
2)预测结果呈“S”型,因此从kog(odds)向概率转化的过程是非线性的,在两端随着log(odds)值的变化,概率变化很小,边际值太小,slope太小,而中间概率的变化很大,很敏感,导致很多区间的变量变化对目标概率的影响没有区分度,无法确定阈值。
8、LR和SVM
1)LR采用log损失,SVM采用合页损失
2)LR对异常值敏感,SVM对异常值不敏感
3)在训练集较小时,SVM较适用,而LR需要较多的样本
4)LR模型找到的超平面,是尽量让所有点都远离他,而SVM寻找的超平面是只让最靠近中间分割线的支持向量远离他,即只用到了支持向量样本。
5)对非线性问题的处理方式不同,LR主要靠特征构造,必须组合交叉特征,特征离散化。SVM也可以这样,但是主要通过核函数
6)SVM更多的属于非参数模型,而LR是参数模型,本质不同。
9、那怎么根据特征数量和样本量来选择SVM和LR模型呢?
1)如果特征的数量很大,跟样本量差不多,这时候选用LR或者是Linear Kernel的SVM
2)如果特征的数量比较小,样本数量一般,不算大也不算小,选用SVM+Gassian Kernel
3)如果特征的数量比较小,而样本数量很多,需要手工添加一些特征变成第一种情况。
注意:LR和不带核函数的SVM比较类似