本次赛题需要利用历史某3年的汽车日上牌数据,预测某2年每天的汽车上牌数。初赛将挑选出5个汽车品牌,给出这些品牌每天的上牌数,当天是星期几,来预测5个汽车品牌未来每天的上牌总数。
数据说明
1、数据分成训练数据(train.txt)和测试数据(test.txt)。其中

前3个字段是特征变量,”cnt“是目标变量
2、数据经过严格脱敏,所以选手看到的”cnt”并非真值;字段“date”,“brand”用数字替代;字段“day_of_week”是真实的数据
3、排名结果依据预测结果的MSE
选手需要提交测试数据的预测结果,共2列:
【题目分析】
首先,本次比赛的题目是一个预测问题,从过去数据中找到某种规则并对之后的事件进行预测。
其次,从训练集可以看到,每条样本有四个属性,date是从1到n的连续值;day_of_week是一个离散属性,属性值包含1到7;brand也是一个离散属性,属性值包含1到5;cnt即为我们的目标属性也就是当天的汽车上牌量(整数)
请注意:提交结果只需要预测当天物种测量的总上牌量即可,而 并不需要预测出5中车辆相应的上牌量。
【本文方法】
通过探索性分析找出样本潜在属性来替代date,将预测问题转化为一个回归问题,将最后的预测值取整得到结果
一般数据挖掘流程
1、定义问题:即分析问题,确定问题的属性
2、收集数据:本次竞赛已经给出数据集,在网站下载即可
3、数据清洗:经数据集中的缺失项、异常值进行优化处理,保证后续工作正常展开
4、进行探索性分析(EDA):通过图形化数据分析找出潜在问题
5、模型选择:即选择与问题相匹配的机器学习算法
6、模型拟合与优化处理
【探索性分析】
1、先将同一天的汽车上上牌数量求出来;这一步将得到一个表格,每个样本只有三个属性 ,即date、day_of_week、cnt(当天上牌数总量)
2、接下来将该表格每天的上牌量进行散点图展示,利用matplotlib库中的scatter函数,散点结果如下:
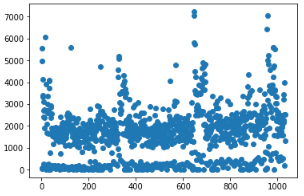
可以看出由于训练集是收集了三年的上牌信息,所以数据呈现一定的周期性
3、与此同时,数据也呈现了一定的断层,也就是500以下有一部分样本,1000以上有一部分样本,考虑到周末与工作日节假日的区别,这些区别可能是导致了上牌量的极端分布,因此做了将工作日和周六周日进行分开散点,散点如下:
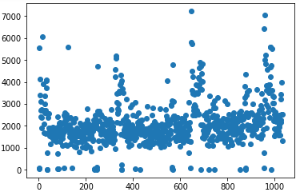
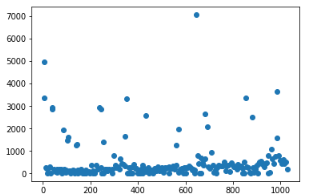
可以看到,工作日与周六周日的影响因素确实很大,但在某些点也出现了异常点,也就是三年内有几个工作日上牌量极少,而有几个周六或者周日上牌量特别高,考虑到我国国情,有三八妇女节、五一劳动节、六一儿童节,十一国庆七天假、清明中秋等传统节日以及圣诞节等国外节日所在星期不固定所导致以上情况。
4、由于箱型图信息量大,对异常值敏感等优点,接下来对星期1-7绘制箱型图,从而观察异常值,图像图下
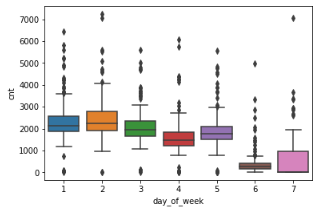
从图中可以看出,工作日五天之间存在细微的差别,周日的数据跨度大需要适度的处理。
【数据预处理】
1、通过阈值的方法剔除异常值;此时的样本适量由原来的1032变成了990了
2、由于给定数据集中样本的date属性域是一个从1到n的离散属性,也就是没有一个样本的date值是唯一的,所以无法用作训练回归模型的自变量,然而除了date就只剩下day_of_week这一个自变量了,为了增加准确率,根据自然法则将样本划分为四个集合,分别表示春夏秋冬,同时考虑到训练集中包含三年的上牌数据,整体手动划分起来具有一定的困难,准确率也无法保障,于是采用了将三年数据通过date折叠成一年,样本数量保持不变,
其中data是之前一步的X,就是剔除掉离群点的训练集,对这个训练集进行散点结果如下:
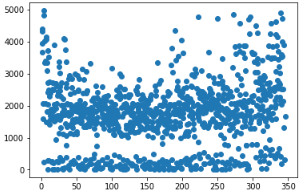
箱型图如下:
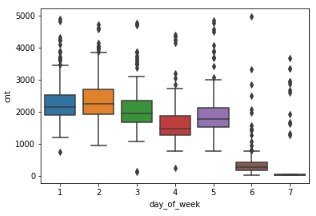
2、接下来给这些样本加上季节属性,
3、接下来进行测试集的预处理(由于训练集只有date和day_of_week两个属性,需要加上季节属性)
【模型选择与拟合】
本文使用的是随机森林中的回归模型,并且通过改变随机种子改变训练计划分策略从而多次建模预测去预测平均值 。
总结:
以上所述的方法还尊在很多不足的地方,比如,对三年样本的折叠策略存在误差;季节划分上存在误差;非周六周日的节假日并没有被考虑在内;迭代次数较少等。