隐马尔科夫模型(Hidden Markov Models)

链接汇总

http://www.csie.ntnu.edu.tw/~u91029/HiddenMarkovModel.html 演算法笔记

http://read.pudn.com/downloads133/doc/fileformat/568756/HMM-DL.pdf本文讲述了 HMM原理，方法，典型应用

http://www.cnblogs.com/tsingke/p/3923169.html  HMM（隐马尔科夫模型）基本原理及其实现

http://wenku.baidu.com/link?url=gDyHVznPs6c61PyoULDFQRzmXLJ2btVNJjlF-vMqRrC9gaNMOcq4j6a0hsSFMNkfwK9en-Jyb74VxDnvvlNdD3zmOsIl_nZKJq2n87nsNbi

http://danielroggen.net/software_dhmm.html 离散的马尔科夫模型

http://www.ncbi.nlm.nih.gov/pubmed/24489371    （StochHMM: a flexible hidden Markov model tool and C++ library）下载https://github.com/KorfLab/StochHMM

http://www.kanungo.com/software/software.html#umdhmm         Hidden Markov Model (HMM) Software

https://github.com/castl/PSLRHmm     A parallel sparse left-right hidden markov model c++ library.

http://www.cs.au.dk/~asand/?page_id=152   HMMlib is a C++ library for constructing and analyzing general hidden Markov models.

隐马尔科夫模型是建立在几个假设条件下的，做假设是为了简化模型。

• 介绍（introduction)
• 生成模式（Generating Patterns）
• 隐含模式（Hidden Patterns）
• 隐马尔科夫模型（Hidden Markov Models）
• 前向算法（Forward Algorithm）
• 维特比算法（Viterbi Algorithm）
• 前向后向算法（Forward-Backward Algorithm）
• 总结

---

介绍（introduction）

通常我们总是对寻找某一段时间上的模式感兴趣，这些模式可能出现在很多领域：一个人在使用电脑的时候使用的命令的序列模式；一句话中的单词的序列；口语中的音素序列。总之能产生一系列事件的地方都能产生有用的模式。

考虑一个最简单的情况：有人(柯南？)试图从一块海藻来推断天气的情况。一些民间的传说认为“soggy”的海藻意味着潮湿（wet）的天气，“dry”的海藻预示着晴朗（sun）。如果海藻处于中间状态“damp”，那就无法确定了。但是，天气的情况不可能严格的按照海藻的状态来变化，所以我们可以说在一定程度上可能是雨天或是晴天。另一个有价值的信息是之前某些天的天气情况，结合昨天的天气和可以观察到的海藻的状态，我们就可以为今天的天气做一个较好的预报。

这是在我们这个系列的介绍中一个非常典型的系统。

• 首先我们介绍一个可以随时间产生概率性模型的系统，例如天气在晴天或者雨天之间变动。
• 接下来我们试图去预言我们所不能观察到的"隐形"的系统状态，在上面的例子中，能被观察到的序列就是海藻的状态吗，隐形的系统就是天气情况
• 然后我们看一下关于我们这个模型的一些问题，在上面那个例子中，也许我们想知道

1. 如果我们观察一个星期每一天的海藻的状态，我们是否能知相应的其天气情况
2. 如果给出一个海藻状态的序列，我们是否能判断是冬天还是夏天？我们假设，如果海藻干（dry）了一段时间，那就意味着是夏天如果海藻潮湿（soggy）了一段时间，那可能就是冬天。

---

生成模式（Generating Patterns）

 

• 确定的模式（Deterministic Patterns）

考虑交通灯的例子，一个序列可能是红-红/橙-绿-橙-红。这个序列可以画成一个状态机，不同的状态按照这个状态机互相交替

我们可以注意到，每一个状态都只依赖于此前的状态，如果当前的是绿灯，那么接下来就是橙灯，这就是一个确定型的系统。确定型的系统更容易理解和分析，只要这些状态转移都是已知的。

• 不确定的模式（Non-Deterministic Patterns）

为了让之前那个天气的例子更贴近现实，我们可以添加一个状态-多云。和交通灯的例子不同，我们不能得到一个确定的状态转移系统，但是我们还是希望能得到一个天气的模式。

一种办法就是假设这个模型的每个状态都只依赖于之前的状态，这个假设被称为马尔科夫假设，这个假设可以大大的简化这个问题。显然，这个假设可能是一个非常糟糕的假设，导致很多重要的信息都丢失了。

当涉及到天气的时候，马尔科夫假设假设如果我们知道之间一些天的天气的信息，不考虑风力、气压等因素，那么我们就能预言今天的天气。当然，和其他许多例子一样，这个列子也是不合实际的。但是，这样一个简化的系统可以有利于我们的分析，所以我们通常接受这样的假设，因为我们知道这样的系统能让我们获得一些有用的信息，尽管不是十分准确的。

一个马尔科夫过程就是指过程中的每个状态的转移只依赖于之前的n个状态，这个过程被称为1个n阶的模型，其中n是影响转移的状态的数目。最简单的马尔科夫过程就是一阶过程，每一个状态的转移只依赖于其之间的那一个状态。注意这和确定型的系统不一样，因为这种装因是有概率的，而不是确定的。下面这个图展示了天气这个例子中所有可能的一阶转移：

注意一个含有M个状态的一阶过程有M的平方个状态转移。每一个转移的概率叫做状态转移概率（state transition probability），就是从一个状态转移到另一个状态的概率。这所有的M的平方个概率可以用一个状态转移矩阵来表示。注意这里有一个假设，概率不随时间的变化而变化，这又是一个不现实但很重要的假设。下面就是一个状态转移矩阵的列子：

这个矩阵的意思是，如果昨天是晴天，那么今天又50%的可能是晴天，37.5%的概率是阴天，12.5%的概率会下雨，很明显，每一行的和都是1。

为了初始化这样一个系统，我们需要一个初始的概率向量：

这个向量表示第一天是晴天。

到这里，我们就为一阶马尔科夫过程定义了以下三个部分:

• 状态：晴天、阴天和下雨
• 初始向量：定义系统在时间为0的时候的状态的概率
• 状态转移矩阵：每种天气转换的概率

所有的能被这样描述的系统都是一个马尔科夫过程。

• 总结（Summary）

我们为了找到随时间变化的模式，就试图去建立一个可以产生模式的过程模型。我们使用了具体的时间步骤、状态、并且做了马尔科夫假设。有了这些假设，这个能产生模式系统就是一个马尔科夫过程。一个马尔科夫过程包括一个初始向量和一个状态转移矩阵。关于这个假设需要注意的一点是状态转移概率不随时间变化。

隐含模式（Hidden Patterns）

当马尔科夫过程不够强大的时候，我们又该怎么办呢？

在某些情况下马尔科夫过程不足以描述我们希望发现的模式。回到之前那个天气的例子，一个隐居的人可能不能直观的观察到天气的情况，但是有一些海藻。民间的传说告诉我们海藻的状态在某种概率上是和天气的情况相关的。在这种情况下我们有两个状态集合，一个可以观察到的状态集合（海藻的状态）和一个隐藏的状态（天气的状况）。我们希望能找到一个算法可以根据海藻的状况和马尔科夫假设来预测天气的状况。

一个更现实的例子是语音识别，我们听到的声音是声带、喉咙和一起其他的发音器官共同作用的结果。这些因素相互作用，共同决定了每一个单词的声音，而一个语音识别系统检测的声音（可以观察的状态）是人体内部各种物理变化（隐藏的状态、引申一个人真正想表达的意思）产生的。

某些语音识别设备把内部的发音机制作为一个隐藏的状态序列，把最后的声音看成是一个和隐藏的状态序列十分相似的可以观察到的状态的序列。在这两个例子中，一个非常重要的地方是隐藏状态的数目和可以观察到的状态的数目可能是不一样的。在一个有三种状态的天气系统（sunny、cloudy、rainy）中，也许可以观察到四种潮湿程度的海藻（dry、dryish、damp、soggy）。在语音识别中，一个简单的发言也许只需要80个语素来描述，但是一个内部的发音机制可以产生不到80或者超过80种不同的声音。

在上面的这些情况下，可以观察到的状态序列和隐藏的状态序列是概率相关的。于是我们可以将这种类型的过程建模为又一个隐藏的马尔科夫过程和一个和这个马尔科夫过程概率相关的并且可以观察到的状态集合。

下图显示了天气的例子中隐藏的状态和可以观察到的状态之间的关系。我们假设隐藏的状态是一个简单的一阶马尔科夫过程，并且他们两两之间都可以相互转换。

隐藏的状态和可以观察到的状态之间有一种概率上的关系，也就是说某种隐藏状态H被认为是某个可以观察的状态O1是有概率的，假设为P（O1|H）。如果可以可以观察的状态有三种，那么很显然P（O1|H）+ P（O2|H）+ P（O3|H） = 1。这里我和原文的意思不太相同，原文说的意思是P（O1|H1）+ P（O1|H2）+P（O1|H3）= 1，但是这和下面的例子又不同。

这样，我们也可以得到一个另一个矩阵，称为混淆矩阵。这个矩阵的内容是某个隐藏的状态被分别观察成集中不同的可以观察的状态的概率，在天气的例子中，这个矩阵如下图：

注意到图中每一行的和为1，但是每一列的和不为1，这里我觉得可能是原文出错了，或者隐藏状态还有其他。

总结

我们已经看到有一些过程是和一个隐藏的马尔科夫过程概率相关的。在这种情况下，可以观察到的状态和隐藏的状态的数目可能是不一样的。我们可以把这种过程建模为隐马尔科夫模型（HMM）。这个模型包含两个状态集合和三个概率集合。

• 隐藏的状态：一个隐藏的马尔科夫过程
• 可以观察到的状态：如名
• 初始向量：初始状态的隐藏状态的概率
• 状态转移矩阵：隐藏状态的状态转移概率
• 混淆矩阵：隐藏状态被观察成各个可以观察到的状态的概率

我们可以认为隐马尔科夫模型是在一个不可观察的马尔科夫过程上添加了一个可以观察到的状态集合，加上这个过程到这个集合的一些概率关系得到的。

隐马尔科夫模型（Hidden Markov Models）

定义

隐马尔科夫模型可以用一个三元组(π,A,B)来定义:

1. π 表示初始状态概率的向量
2. A =（aij）（隐藏状态的）转移矩阵  P（Xit|Xj（t-1））  t-1时刻是j而t时刻是i的概率
3. B =（bij）混淆矩阵  P（Yi|Xj） 在某个时刻因隐藏状态为Xj而观察状态为Yi的概率

值得注意的是，在状态转移矩阵中的每个概率都是时间无关的，也就是说我们假设这个概率是固定的，不随时间变化。当然，这是马尔科夫模型最不切合实际的一个假设。

隐马尔科夫模型的使用

如果一个模型可以被描述成一个隐马尔科夫模型，有三个问题可以得到解决。前两个是模式识别的问题：1）根据隐马尔科夫模型得到一个可观察状态序列的概率（评价）；2）找到一个隐藏状态的序列使得这个序列产生一个可观察状态序列的概率最大(解码)。第三个问题就是根据一个可以观察到的状态序列集产生一个隐马尔科夫模型（学习）。

1.评价

假设我们有很多隐马尔科夫模型（也就是说一个三元组的集合）描述不同的系统和一个可观察状态序列集。我们也许想知道哪一个隐马尔科夫模型最可能产生某个可观察状态序列。比如说，我们也许有一个海藻的“Summer”模型和一个“Winter”模型，因为海藻在夏天和冬天的状态应该是不同的，我们希望根据一个可观察状态（海藻的潮湿与否）序列来判断现在是夏天还是冬天。

我们可以使用前向算法来计算在某个特定的HMM下一个可观察序列的概率，然后据此找到最可能的模型。

这种类型的应用通常出现在语音设别中，通常我们会使用很多HMM，每一个针对一个特别的单词。一个可观察状态的序列是从一个可以听到的单词向前得到的，然后这个单词就可以通过找到满足这个可观察状态序列的最大概率的HMM来识别。

2.解码

根绝可观察状态的序列找到一个最可能的隐藏状态序列。

和上面一个问题相似的并且更有趣的是根据可观察序列找到隐藏序列。在很多情况下，我们队隐藏状态更有兴趣，因为其包含了一些不能被直接观察到的有价值的信息。比如说在海藻和天气的例子中，一个隐居的人只能看到海藻的状态，但是他想知道天气的状态。这时候我们就可以使用Viterbi算法来根据可观察序列得到最优可能的隐藏状态的序列，当然前提是已经有一个HMM。

另一个广泛使用Viterbi算法的领域是自然语言处中标引词性。句子中的单词是可以观察到的，词性是隐藏的状态。通过根据语句的上下文找到一句话中的单词序列的最有可能的隐藏状态序列，我们就可以得到一个单词的词性（可能性最大）。这样我们就可以用这种信息来完成其他一些工作。

3.学习

从一个观察集中得到一个隐马尔科夫模型。

第三个问题也是最困难的问题，根绝观察到的序列集来找到一个最有可能的HMM，也就是说确定一个最有可能的三元组(π,A,B）。当A，B矩阵都不是直观可测量（通过经验得到）的的时候，可以使用前向后向算法来解决这个问题。

总结

尽管做出了一些不太符合实际的假设，但是用三元组描述的HMMs在描述真实系统并进行分析的时候具有很大的价值，并且可以解决下面这些问题：

1. 用前向算法找到最有可能的隐马尔科夫模型
2. 用Viterbi算法根据观察序列找到最有可能的隐藏序列
3. 用前向后向算法决定最有可能产生某个观察集的隐马尔科夫模型的参数

前向算法(Forward Algorithm)

一、如果计算一个可观察序列的概率？  

1.穷举搜索

 加入给定一个HMM，也就是说(,A,B)这个三元组已知，我们想计算出某个可观察序列的概率。考虑天气的例子，我们知道一个描述天气和海藻状态的HMM，而且我们还有一个海藻状态的序列。假设这个状态中的某三天是（dry，damp，soggy），在这三天中的每一天，天气都可能是晴朗，多云或者下雨，我们可以用下图来描述观察序列和隐藏序列：

在这个图中的每一列表示天气的状态可能，并且每个状态都指向相邻的列的每个状态，每个状态装换在状态转移矩阵中都有一个概率。每一列的下面是当天的可观察的海藻的状态，在每种状态下出现这种可观察状态的概率是由混淆矩阵给出的。

一个可能的计算可观察概率的方法是找到每一个可能的隐藏状态的序列，这里有3^3 = 27种，这个时候的可观察序列的概率就是 Pr(dry,damp,soggy | HMM) = Pr(dry,damp,soggy | sunny,sunny,sunny) + Pr(dry,damp,soggy | sunny,sunny ,cloudy) + Pr(dry,damp,soggy | sunny,sunny ,rainy) + . . . . Pr(dry,damp,soggy | rainy,rainy ,rainy)。

很显然，这种计算的效率非常低，尤其是当模型中的状态非常多或者序列很长的时候。事实上，我们可以利用概率不随时间变化这个假设来降低时间的开销。

2.使用递归来降低复杂度

我们可以考虑给定HMM的情况下，递归的计算一个可观察序列的概率。我们可以首先定义一个部分概率，表示达到某个中间状态的概率。接下来我们将看到这些部分概率是如何在time=1和time = n（n > 1）的时候计算的。

假设一个T时间段的可观察序列是：

2a.部分概率

下面这张图表示了一个观察序列（dry，damp，soggy）的一阶转移

我们可以通过计算到达某个状态的所有路径的概率和来计算到达某个中间状态的概率。比如说，t = 2时刻clody的概率用三条路径的概率之和来表示：

我们用t(j)来表示在t时刻是状态j的概率，t ( j )= Pr( observation | hidden state is j ) x Pr(all paths to state j at time t)。

最后一个观察状态的部分概率就表示了整个序列最后达到某个状态的所有可能的路径的概率和，比如说在这个例子中，最后一列的部分状态

是通过下列路径计算得到的：

因为最后一列的部分概率是所有可能的路径的概率和，所以就是这个观察序列在给定HMM下的概率了。

2b.计算 t = 1时候的部分概率

计算部分概率的公式是： t ( j )= Pr( observation | hidden state is j ) x Pr(all paths to state j at time t)

当t = 1的时候，没有路径到某个状态，所以这里是初始概率， Pr( state | t = 1) = (state)，这样我们就可以计算t=1时候的部分概率为：

因为在初始的时候，是状态j的概率不仅和这个状态本身相关，还和观察状态有关，所以这里用到了混淆矩阵的值，k1表示第一个观察状态，bjk1表示隐藏状态是j，但是观察成k1的概率。

2c.计算t > 1时候的部分概率

还是看计算部分概率的公式： t ( j )= Pr( observation | hidden state is j ) x Pr(all paths to state j at time t)

这个公式的左边是从混淆矩阵中已知的，我只需要计算右边部分，很显然右边是所有路径的和：

需要计算的路径数是和观察序列的长度的平方相关的，但是t时刻的部分概率已经计算过了之前的所有路径，所以在t+1时刻只需要根据t时刻的概率来计算就可以了：

这里简单解释下，bjkt+1 就是在t+1时刻的第j个隐藏状态被认为是当前的观察状态的概率，后面一部分是所有t时刻的隐藏状态到t+1时候的隐藏状态j的转移的概率的和。这样我们每一步的计算都可以利用上一步的结果，节省了很多时间。

2d.降低计算复杂度

我们可以比较穷举和递归算法的复杂度。假设有一个HMM l  =(,A,B)，其中有n个隐藏状态，我们有一个长度为T的观察序列。

穷举算法的需要计算所有可能的隐藏序列：

需要计算：

很显然穷举算法的时间开销是和T指数相关的，而如果采用递归算法，由于我们每一步都可以利用上一步的结果，所以是和T线性相关的。（这里认为n是一个常数）

3.总结

这里我们的目的是在某个给定的HMM下，计算出某个可观察序列的概率。我们通过先计算部分概率的方式递归的计算整个序列的所有路径的概率，大大节省了时间。在t=1的时候，使用了初始概率和混淆矩阵的概率，而在t时刻的概率则可以利用t - 1时刻的结果。

二、前向算法的定义

我们使用前向算法去计算T长度序列的概率：

每一个y就是观察状态。在t=1时刻的中间节点的部分状态可以用下面的公式计算：

对于t>1的情况，部分概率的计算可以用下面的公式：

这里，我觉得是原作者的笔误，后面的应该是bjkt+1

这样我们就可以用递归的方式来计算所有可能的路径的概率和，最后，所有的部分概率的计算公式为

使用天气的例子，计算t = 2时刻的cloud状态的概率方法如图：

三、总结

我们使用前向算法在给定的一个HMM下计算某个可观察序列的概率。前向算法主要采用的是递归的思想，利用之前的计算结果。有了这个算法，我们就可以在一堆HMM中，找到一个最满足当前的可观察序列的模型（前向算法计算出来的概率最大）。

维特比算法(Viterbi Algorithm)

找到可能性最大的隐藏序列

通常我们都有一个特定的HMM，然后根据一个可观察序列去找到最可能生成这个可观察序列的隐藏序列。

1.穷举搜索

我们可以在下图中看到每个状态和观察的关系。

通过计算所有可能的隐藏序列的概率，我们可以找到一个可能性最大的隐藏序列，这个可能性最大的隐藏序列最大化了Pr(observed sequence | hidden state combination)。比如说，对于上图中的可观察序列（dry damp soggy），最可能的隐藏序列就是下面这些概率中最大的：

Pr(dry,damp,soggy | sunny,sunny,sunny), Pr(dry,damp,soggy | sunny,sunny,cloudy), Pr(dry,damp,soggy | sunny,sunny,rainy), . . . . Pr(dry,damp,soggy | rainy,rainy,rainy)

这个方法是可行的，但是这种计算的代价是昂贵。和前向算法一样，我们可以利用转移概率在时间上的不变性来降低计算的复杂度。

2.使用递归降低复杂度

在给定了一个可观察序列和HMM的情况下，我们可以考虑递归的来寻找最可能的隐藏序列。我们可以先定义一个部分概率，既是到达某个中间状态的概率。接下来我们将讨论如果计算t = 1和t = n（ n > 1）的部分概率。

注意这里的部分概率和前向算法中的部分概率是不一样的，这里的部分概率表示的是在t时刻最可能到达某个状态的一条路径的概率，而不是所有概率之和。

2a.部分概率和部分最优路径

考虑下面这个图以及可观察序列（dry，damp，soggy）的一阶转移

对于每一个中间状态和终止状态（t = 3）都有一个最可能的路径。比如说，在t=3时刻的三个状态都有一个如下的最可能的路径：

我们可以称这些路径为部分最优路径。这些部分最优路径都有一个概率，也就是部分概率。和前向算法中的部分概率不一样，这里的概率只是一个最可能路径的概率，而不是所有路径的概率和。

 我们可以用 (i,t)来表示在t时刻，到状态i的所有可能的序列（路径）中概率最大的序列的概率，部分最优路径就是达到这个最大概率的路径，对于每一个时刻的没一个状态都有这样一个概率和部分最优路径。

最后，我们通过计算t = T时刻的每一个状态的最大概率和部分最优路径，选择其中概率最大的状态和它的部分最优路径来得到全局的最优路径。

2b.计算t = 1时刻的部分概率

当t=1时刻的时候，到达某个状态最大可能的路径还不存在，但是我们可以直接使用在t=1时刻某个状态的概率和这个状态到可观察序列k1的转移概率：

2c.计算t >1 时刻的部分概率

接下来我们可以根据t - 1时刻的部分概率来求t 时刻的部分概率

我们可以计算所有到状态X的路径的概率，找到其中最可能的路径，也就是局部最优路径。注意到这里，到达X的路径必然会经过t - 1时刻的A、B和C，所以我们可以利用之前的结果。达到X的最可能的路径就是下面三个之一：

(sequence of states), . . ., A, X (sequence of states), . . ., B, X or (sequence of states), . . ., C, X

我们需要做的就是找到以AX、BX和CX结尾的路径中概率最大的那个。

根据一阶马尔科夫的假设，一个状态的发生之和之前的一个状态有关系，所以X在某个序列的最后发生的概率只依赖于其之前的一个状态：

Pr (most probable path to A) . Pr (X | A) . Pr (observation | X)

有个了这个公式，我们就可以利用t - 1时刻的结果和状态转移矩阵和混淆矩阵的数据：

将上面这个表达式推广一下，就可以得到t时刻可观察状态为kt的第i个状态的最大部分概率的计算公式：

其中aji表示从状态j转移到状态i的概率，bikt表示状态i被观察成kt的概率。

2d.后向指针

考虑下图

在每一个中间状态和结束状态都有一个部分最优概率 (i,t)。但是我们的目的是找到最可能的隐藏状态序列，所以我们需要一个方法去记住部分最优路径的每一个节点。

考虑到要计算t时刻的部分概率，我们只需要知道t-1时刻的部分概率，所以我们只需要记录那个导致了t时刻最大部分概率的的状态，也就是说，在任意的时刻，系统都必须处在一个能在下一时刻产生最大部分概率的状态。我们可以利用一个后向指针来记录导致某个状态最大部分概率的上一个状态，形式化的描述为：

这里argmax表示能最大化后面公式的j值，同样可以发现这个公式之和t-1时刻的部分概率和转移概率有关，因为后向指针只是为了找到“我从哪里来”，这个问题和可观察没有关系，所以这里不需要再乘上混淆因子。

2e.优点

使用viterbi算法对一个可观察状态进行解码有两个重要的优点：

1. 通过使用递归来减少复杂度，这点和之前的前想算法是一样的
2. 可以根据可观察序列找到最优的隐藏序列，这个的计算公式是：

where

这里就是一个从左往右翻译的过程，通过前面的翻译结果得到后面的结果，起始点是初始向量。

2.补充

但在序列某个地方有噪声干扰的时候，某些方法可能会和正确答案相差的较远。

但是Viterbi算法会查看整个序列来决定最可能的终止状态，然后通过后向指针来找到之前的状态，这对忽略孤立的噪声非常有用。

3.总结

Viterbi算法提供了一个根据可观察序列计算隐藏序列的很高效的方法，它利用递归来降低计算复杂度，并且使用之前全部的序列来做判断，可以很好的容忍噪声。

在计算的过程中，这个算法计算每一个时刻每一个状态的部分概率，并且使用一个后向指针来记录达到当前状态的最大可能的上一个状态。最后，最可能的终止状态就是隐藏序列的最后一个状态，然后通过后向指针来查找整个序列的全部状态。

---

前向后向算法（Forward-Backward Algorithm）

和隐马尔科夫模型相关的有趣的问题就是判断一个模型的实用性（前向算法）和找到一个隐藏在可观察序列背后的隐藏序列（Viterbi算法）。当然，这两个过程都需要知道HMM的一些信息，比如转移矩阵，混淆矩阵以及初始的π向量。

但是在很多实际的情况下，HMM不能被直接的判断，这就变成了一个学习问题，前向后向算法可以根据一系列可观察序列来对HMM进行评测。一个可能的例子就是一个很大的语音处理数据库，语音序列可能被建模为一个马尔科夫链，可观察的序列可以被建模为可识别的状态，但是不能直接获得一些其他的相关信息。

前向后向算法理解起来并不困难，但是却要比前向算法和Viterbi算法要复杂，所以这里我们不再详细的介绍。总的来说，这个算法先对一些参数进行猜测，然后再通过评估这些参数的价值来修改这些参数，使得和给定的训练数据的误差变小，这其实是机器学习中的梯度下降的思想。

前向后向算法的名称来源于对于每一个状态，这个算法既要计算到达这一状态的前一个状态的概率，也要计算产生终止状态的后向状态的概率，这两个概率都可以通过递归的方法来实现。对HMM参数的调整可以提高中间概率的准确性，并且这些调整是算法迭代的基础。

---

总结（summary）

通常一个特别的模式不是单独的出现，而是作为某一个时间段下的序列出现。对于以时间为单位的过程有一个假设，一个状态的出现之和其前N个时间单位的状态有关系，这样就是一个N阶马尔科夫链，最简单的情况就是一阶马尔科夫链。

很多情况下，真实的状态序列是不能被直接观察到的，但是可以在一定概率下被间接观察到，这个观察的结果就是另一个可观察的序列，这样我们就可以定义一个隐马尔科夫模型，这个模型在现在的某些领域体现了很大的价值，尤其是语音识别。

这种关于真实序列的模型有三个相关的问题：

1. 评价：一个给定的模型在多大的概率下能产生某个可观察的序列，这个问题可以用前向算法来解决。
2. 解码：给定一个模型和某个可观察序列，最可能的隐藏序列是什么，这个问题可以用Viterbi算法来解决。
3. 学习：给定某个可观察序列，怎么知道这个模型的一些参数，这个问题可以用前向后向算法来解决。

隐马尔科夫模型在分析真实系统的时候表现出了巨大的价值，但是它也有一些缺点，一个最大的缺点就是由于之前的假设导致的过于简化——一个状态只依赖其之间的状态，而且这种依赖是时间无关的。

一个更详细的关于HMMs的介绍可以参见

L R Rabiner and B H Juang, `An introduction to HMMs', iEEE ASSP Magazine, 3, 4-16.

原文：http://blog.csdn.net/eaglex/article/details/6376826

隐马尔可夫模型的评估问题(前向算法）

http://www.cnblogs.com/kaituorensheng/archive/2012/12/01/2797230.html

隐马模型的评估问题即，在已知一个观察序列O=O₁O₂...O_T，和模型μ=（A,B,π}的条件下，观察序列O的概率，即P(O|μ}

                   

      如果穷尽所有的状态组合，即S₁S₁...S₁, S₁S₁...S₂, S₁S₁...S₃, ..., S₃S₃...S₃。这样的话t₁时刻有N个状态，t₂时刻有N个状态...t_T时刻有N个状态，这样的话一共有N*N*...*N= N^T种组合，时间复杂度为O(N^T),计算时，就会出现“指数爆炸”，当T很大时，简直无法计算这个值。为解决这一问题，Baum提出了前向算法。

      归纳过程

      首先引入前向变量α_t(i):在时间t时刻，HMM输出序列为O₁O₂...O_T,在第t时刻位于状态s_i的概率。

      当T=1时，输出序列为O₁,此时计算概率为P(O₁|μ）：假设有三个状态（如下图）1、2、3，输出序列为O₁，有三种可能一是状态1发出，二是从状态2发出，三是从状态3发出。另外从状态1发出观察值O₁得概率为b₁(O₁),从状态2发出观察值O₁得概率为b₂(O₁),从状态3发出观察值O₁得概率为b₃(O₁)。因此可以算出

     P(O₁|μ）= π₁*b₁(O₁)+π₂*b₂(O₁) +  π₃*b₃(O₁)= α₁(1) + α₁(2) + α₁(3)

                                     

      当T=2时，输出序列为O₁O₂,此时计算概率为P(O₁O₂|μ）：假设有三个状态（如下图）1、2、3，输出序列为O₁，有三种可能一是状态1发出，二是从状态2发出，三是从状态3发出。另外从状态1发出观察值O₂得概率为b₁(O₂),从状态2发出观察值O₂得概率为b₂(O₂),从状态3发出观察值O₂得概率为b₃(O₂)。

      要是从状态1发出观察值O₂，可能从第一时刻的1、2或3状态装换过来，要是从状态1转换过来，概率为α₁(1)*a₁₁*b₁(O₂),要是从状态2转换过来，概率为α₁(2)*a₂₁*b₁(O₂),要是从状态3转换过来，概率为α₁(3)*a₃₁*b₁(O₂),因此

     P(O₁O_2,q₂₌s₁|μ）= α₁(1)*a₁₁*b₁(O₂)  + α₁(2)*a₂₁*b₁(O₂) + α₁(3)*a₃₁*b₁(O₂)=α₂(1)

                                     

      同理：P(O₁O_2,q₂₌s₁|μ）= α₁(1)*a₁₂*b₂(O₂)  + α₁(2)*a₂₂*b₂(O₂) + α₁(3)*a₃₂*b₂(O₂)=α₂(2)

               P(O₁O_2,q₂₌s₁|μ）= α₁(1)*a₁₃*b₁(O₂)  + α₁(2)*a₂₃*b₃(O₂) + α₁(3)*a₃₃*b₃(O₂)=α₂(3)

     所以：P(O₁O₂|μ）=P(O₁O_2,q₂₌s₁|μ）+ P(O₁O_2,q₂₌s₁|μ）+ P(O₁O_2,q₂₌s₁|μ）

                             =α₂(1) + α₂(2) + α₂(3)

      以此类推。。。

      前向算法

       step1 初始化：α₁(i) = π_i*b_i(O₁), 1≤i≤N

       step2 归纳计算:

                           

       step3 终结：

                      P(O|μ）=

      时间复杂度

      计算某时刻的某个状态的前向变量需要看前一时刻的N个状态，此时时间复杂度为O(N),每个时刻有N个状态，此时时间复杂度为N*O(N)=O(N²),又有T个时刻，所以时间复杂度为T*O(N²)=O(N²T)。

      程序例证

       

        前向算法计算P(O|M)：

        step1：α₁(1) =π₁*b₁(red)=0.2*0.5=0.1          α₁(2)=π₂*b₂(red)==0.4*0.4= 0.16          α₁(3)=π₃*b₃(red)==0.4*0.7=0.21

        step2：α₂(1)=α₁(1)*a₁₁*b₁(white) + α₁(2)*a₂₁*b₁(white) + α₁(3)*a₃₁*b₁(white)

                     ...

        step3:P(O|M) = α₃(1)+α₃(2)+α₃(3)

        程序代码

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

int main()
{
        float a[3][3] = {{0.5,0.2,0.3},{0.3,0.5,0.2},{0.2,0.3,0.5}};
        float b[3][2] = {{0.5,0.5},{0.4,0.6},{0.7,0.3}};
        float alpha[4][3];
        int i,j,k, count = 1;
        //output list
        int list[4] = {0,1,0,1};
        //step1:Initialization
        alpha[0][0] = 0.2 * 0.5;
        alpha[0][1] = 0.4 * 0.4;
        alpha[0][2] = 0.4 * 0.7;
        //step2:iteration
        for (i=1; i<=3; i++)
        {
            for(j=0; j<=2; j++)
            {
                alpha[i][j] = 0;
                for(k=0; k<=2; k++)
                {
                   alpha[i][j] += alpha[i-1][k] * a[k][j] * b[j][list[count]];
                }
            }
            count += 1;
        }
       for (i=0; i<=3; i++)
        {
            for(j=0; j<=2; j++)
            {
                printf("a[%d][%d]=%f
",i+1,j+1,alpha[i][j]);
            }
        }
       //step3:end
       printf("Forward:%f
", alpha[3][0]+alpha[3][1]+alpha[3][2]);
       return 0;
}

     运行结果

                 

原文：http://www.cnblogs.com/tsingke/p/3923169.html

HMM基本原理

Markov链：如果一个过程的“将来”仅依赖“现在”而不依赖“过去”，则此过程具有马尔可夫性，或称此过程为马尔可夫过程。马尔可夫链是时间和状态参数都离散的马尔可夫过程。HMM是在Markov链的基础上发展起来的，由于实际问题比Markov链模型所描述的更为复杂，观察到的时间并不是与状态一一对应的，而是通过一组概率分布相联系，这样的模型称为HMM。HMM是双重随机过程：其中之一是Markov链，这是基本随机过程，它描述状态的转移，是隐含的。另一个随机过程描述状态和观察值之间的统计对应关系，是可被观测的。

HMM的定义：

HMM实际上是分为两个部分的，一是马尔可夫链，由参数，A描述，它利用一组与概率分布相联系的状态转移的统计对应关系，来描述每个短时平稳段是如何转变到下一个短时平稳段的，这个过程产生的输出为状态序列；二是一个随机过程，描述状态与观察值之间的统计关系，用观察到的序列来描述隐含的状态，由B描述，其产生的输出为观察值序列。

HMM根据其结构的不同可以分为多种类型。根据状态转移概率矩阵的不同，HMM可分为各态遍历模型、从左到右模型、并行路径从左到右模型和无跳转从左到右模型等。根据观察值概率不同，HMM可分为离散HMM、半连续HMM、连续HMM等。

下图是一个典型的HMM：

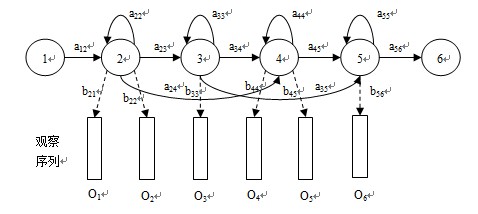
HMM有三个典型的问题:

• 已知模型参数，计算某一特定输出序列的概率，通常使用forward算法解决。
• 已知模型参数，寻找最可能的能产生某一特定输出序列的隐含状态的序列，通常使用Viterbi算法解决。
• 已知输出序列，寻找最可能的状态转移以及输出概率，通常使用Baum-Welch算法以及Reversed Viterbi算法解决。

---

HMM的实现

C语言版：

　　1、 HTK（Hidden Markov Model Toolkit）

　　HTK是英国剑桥大学开发的一套基于C语言的隐马尔科夫模型工具箱，主要应用于语音识别、语音合成的研究，也被用在其他领域，如字符识别和DNA排序等。HTK是重量级的HMM版本。

　　HTK主页：http://htk.eng.cam.ac.uk/

　　2、 GHMM Library

　　The General Hidden Markov Model library (GHMM) is a freely available LGPL-ed C library implementing efficient data structures and algorithms for basic and extended HMMs.

　　GHMM主页：http://www.ghmm.org/

　　3、 UMDHMM（Hidden Markov Model Toolkit）

　　Hidden Markov Model (HMM) Software: Implementation of Forward-Backward, Viterbi, and Baum-Welch algorithms.

　　这款属于轻量级的C语言HMM版本。

　　UMDHMM主页：http://www.kanungo.com/software/software.html

C++版：

　　1、http://www.cs.ualberta.ca/~lindek/hmm.htm

　　2、http://www.shokhirev.com/nikolai/abc/alg/hmm/hmm.html

　　以上两个是C++版本的，但是实现的是离散型的HMM。

Java版：

　　Jahmm Java Library (general-purpose Java library)：

　　Jahmm (pronounced “jam”), is a Java implementation of Hidden Markov Model (HMM) related algorithms. It’s been designed to be easy to use (e.g. simple things are simple to program) and general purpose.

　　Jahmm主页：http://code.google.com/p/jahmm/

Python版：

　　http://www.biocomp.unibo.it/piero/PHMM/

Malab版：

　　Hidden Markov Model (HMM) Toolbox for Matlab：This toolbox supports inference and learning for HMMs with discrete outputs (dhmm’s), 

Gaussian outputs (ghmm’s), or mixtures of Gaussians output (mhmm’s).

　　Matlab-HMM主页：http://www.cs.ubc.ca/~murphyk/Software/HMM/hmm.html

Common Lisp版：

　　CL-HMM Library (HMM Library for Common Lisp)：

　　Simple Hidden Markov Model library for ANSI Common Lisp. Main structures and basic algorithms implemented. Performance speed comparable to C code. It’s licensed under LGPL.

　　CL-HMM主页：http://www.ashrentum.net/jmcejuela/programs/cl-hmm/

Haskell版：

　　The hmm package （A Haskell library for working with Hidden Markov Models）：A simple library for working with Hidden Markov Models. Should be usable even by people who are not familiar with HMMs. Includes implementations of Viterbi’s algorithm and the forward algorithm.

　　Haskell-HMM主页：http://hackage.haskell.org/cgi-bin/hackage-scripts/package/hmm

CDHMM C++版：

　　连续HMM的C++实现：CHMM.rar