算法设计

出处 http://segmentfault.com/blog/exploring/

本章讲解：
1. LCS（最长公共子序列）O(n^2)的时间复杂度,O(n^2)的空间复杂度；
2. 与之类似但不同的最长公共子串方法。
最长公共子串用动态规划可实现O(n^2)的时间复杂度，O(n^2)的空间复杂度；还可以进一步优化，用后缀数组的方法优化成线性时间O(nlogn)；空间也可以用其他方法优化成线性。
3.LIS（最长递增序列）DP方法可实现O(n^2)的时间复杂度，进一步优化最佳可达到O(nlogn)

---

一些定义：
字符串 X， Y 长度 分别m，n

子串：字符串S的子串r[i,...,j],i<=j,表示r串从i到j这一段，也就是顺次排列r[i],r[i+1],...,r[j]形成的字符串

前缀：Xi =﹤x1，⋯，xi﹥ 即 X 序列的前 i 个字符 (1≤i≤m)；
Yj=﹤y1，⋯，yj﹥即 Y 序列的前 j 个字符 (1≤j≤n)；
假定 Z=﹤z1，⋯，zk﹥∈LCS(X , Y)

有关后缀数组的定义

LCS

判断字符串相似度的方法之一 - LCS 最长公共子序列越长，越相似。 算法时间复杂度：O(m*n)
July 10分钟讲LCS视频，

最优子结构性质：
设序列 X=<x1, x2, …, xm> 和 Y=<y1, y2, …, yn> 的一个最长公共子序列 Z=<z1, z2, …, zk>，则：
若 xm=yn，则 zk=xm=yn 且 Zk-1 是 Xm-1 和 Yn-1 的最长公共子序列；
若 xm≠yn 且 zk≠xm ，则 Z是 Xm-1 和 Y 的最长公共子序列；
若 xm≠yn 且 zk≠yn ，则 Z 是X和 Yn-1 的最长公共子序列。

递归结构：

递归结构容易看到最长公共子序列问题具有子问题重叠性质。例如，在计算 X 和 Y 的最长公共子序列时，可能要计算出X 和 Yn-1 及 Xm-1 和 Y 的最长公共子序列。而这两个子问题都包含一个公共子问题，即计算 Xm-1 和 Yn-1 的最长公共子序列。

递归结构容易看到最长公共子序列问题具有子问题重叠性质。例如，在计算 X 和 Y 的最长公共子序列时，可能要计算出X 和 Yn-1 及 Xm-1 和 Y 的最长公共子序列。而这两个子问题都包含一个公共子问题，即计算Xm-1 和 Yn-1 的最长公共子序列。

计算最优值：
子问题空间中，总共只有O(m*n) 个不同的子问题，因此，用动态规划算法自底向上地计算最优值能提高算法的效率。

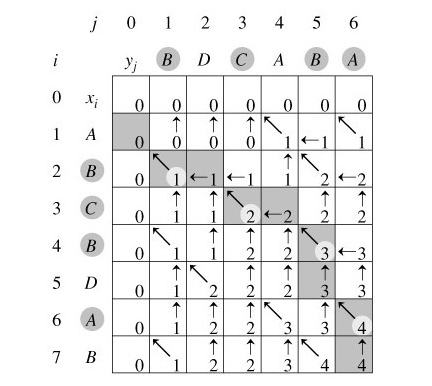
长度表C 和 方向变量B：

java实现：

 /* 动态规划
 * 求最长公共子序列
 * @ author by gsm
 * @ 2015.4.1
 */
import java.util.Random;
public class LCS {

    public static int[][] lengthofLCS(char[] X, char[] Y){
        /* 构造二维数组c[][]记录X[i]和Y[j]的LCS长度 (i,j)是前缀
         * c[i][j]=0; 当 i = j = 0;
         * c[i][j]=c[i-1][j-1]+1; 当 i = j > 0; Xi == Y[i]
         * c[i][j]=max(c[i-1][j],c[i][j+1]); 当 i = j > 0; Xi != Y[i]
         * 需要计算 m*n 个子问题的长度 即 任意c[i][j]的长度
         * -- 填表过程
         */
        int[][]c = new int[X.length+1][Y.length+1];

        // 动态规划计算所有子问题
        for(int i=1;i<=X.length;i++){
            for (int j=1;j<=Y.length;j++){
                if(X[i-1]==Y[j-1]){
                    c[i][j] = c[i-1][j-1]+1;
                }
                else if(c[i-1][j] >= c[i][j-1]){
                    c[i][j] = c[i-1][j];
                }
                else{
                    c[i][j] = c[i][j-1];
                }
            }
        }

        // 打印C数组
        for(int i=0;i<=X.length;i++){
            for (int j=0;j<=Y.length;j++){
                System.out.print(c[i][j]+" ");
            }
            System.out.println();
        }
        return c;
    }
    // 输出LCS序列
    public static void print(int[][] arr, char[] X, char[] Y, int i, int j) {
        if(i == 0 || j == 0)
            return;
        if(X[i-1] == Y[j-1]) {
            System.out.print("element " + X[i-1] + " ");
            // 寻找的
            print(arr, X, Y, i-1, j-1);
        }else if(arr[i-1][j] >= arr[i][j-1]) {
            print(arr, X, Y, i-1, j);
        }else{
            print(arr, X, Y, i, j-1);
        }
    }
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        char[] x ={'A','B','C','B','D','A','B'}; 
        char[] y ={'B','D','C','A','B','A'}; 
        int[][] c = lengthofLCS(x,y);
        print(c, x, y, x.length, y.length);
    }
}

最长公共子串

一个问题

定义 2 个字符串 query 和 text, 如果 query 里最大连续字符子串在 text 中存在，则返回子串长度. 例如: query="acbac"，text="acaccbabb"， 则最大连续子串为 "cba", 则返回长度 3.

方法

时间复杂度：O(m*n)的DP

这个 LCS 跟前面说的最长公共子序列的 LCS 不一样，不过也算是 LCS 的一个变体，在 LCS 中，子序列是不必要求连续的，而子串则是 “连续” 的

我们还是像之前一样 “从后向前” 考虑是否能分解这个问题，在最大子数组和中，我们也说过，对于数组问题，可以考虑 “如何将 arr[0,...i] 的问题转为求解 arr[0,...i-1] 的问题 ”，类似最长公共子序列的分析，这里，我们使用c[i,j] 表示 以 Xi 和 Yj 结尾的最长公共子串的长度，因为要求子串连续，所以对于 Xi 与 Yj 来讲，它们要么与之前的公共子串构成新的公共子串；要么就是不构成公共子串。故状态转移方程

X[i-1] == Y[j-1]，c[i,j] = c[i-1,j-1] + 1； X[i-1] != Y[j-1]，c[i,j] = 0；
对于初始化，i==0 或者 j==0，c[i,j] = 0
代码：

public class LCString {
    public  static int lengthofLCString(String X, String Y){
        /* 构造二维数组c[][]记录X[i]和Y[j]的LCS长度 (i,j)是前缀
         * c[i][j]=0; 当 i = j = 0;
         * c[i][j]=c[i-1][j-1]+1; 当 i = j > 0; Xi == Y[i]
         * c[i][j]=0; 当 i = j > 0; Xi != Y[i]
         * 需要计算 m*n 个子问题的长度 即 任意c[i][j]的长度
         * -- 填表过程
         */
        int[][]c = new int[X.length()+1][Y.length()+1];
        int maxlen = 0;
        int maxindex = 0;
        for(int i =1;i<=X.length();i++){
            for(int j=1;j<=Y.length();j++){
                if(X.charAt(i-1) == Y.charAt(j-1)){
                    c[i][j] = c[i-1][j-1]+1;
                    if(c[i][j] > maxlen)
                    {
                        maxlen = c[i][j];
                        maxindex = i + 1 - maxlen;
                    }
                }
            }
        }
        return maxlen;
    }

    public static void main(String[] args) {
        String X = "acbac";
        String Y = "acaccbabb";
        System.out.println(lengthofLCString(X,Y)); 
    }
}

时间复杂度O(nlogn)的后缀数组的方法

有关后缀数组以及求最长重复子串
前面提过后缀数组的基本定义，与子串有关，可以尝试这方面思路。由于后缀数组最典型的是寻找一个字符串的重复子串，所以，对于两个字符串，我们可以将其连接到一起，如果某一个子串 s 是它们的公共子串，则 s 一定会在连接后字符串后缀数组中出现两次，这样就将最长公共子串转成最长重复子串的问题了，这里的后缀数组我们使用基本的实现方式。

值得一提的是，在找到两个重复子串时，不一定就是 X 与 Y 的公共子串，也可能是 X 或 Y 的自身重复子串，故在连接时候我们在 X 后面插入一个特殊字符‘#’，即连接后为 X#Y。这样一来，只有找到的两个重复子串恰好有一个在 #的前面，这两个重复子串才是 X 与 Y 的公共子串

各方案复杂度对比

设字符串 X 的长度为 m，Y 的长度为 n，最长公共子串长度为 l。

对于基本算法（brute force），X 的子串（m 个）和 Y 的子串（n 个）一一对比，最坏情况下，复杂度为 O(m*n*l)，空间复杂度为 O(1)。

对于 DP 算法，由于自底向上构建最优子问题的解，时间复杂度为 O(m*n)；空间复杂度为 O(m*n)，当然这里是可以使用滚动数组来优化空间的，滚动数组在动态规划基础回顾中多次提到。

对于后缀数组方法，连接到一起并初始化后缀数组的时间复杂度为 O(m+n)，对后缀数组的字符串排序，由于后缀数组有 m+n 个后缀子串，子串间比较，故复杂度为 O((m+n)*l*lg(m+n))，求得最长子串遍历后缀数组，复杂度为 O(m+n)，所以总的时间复杂度为 O((m+n)*l*lg(m+n))，空间复杂度为 O(m+n)。

总的来说使用后缀数组对数据做一些 “预处理”，在效率上还是能提升不少的。

LIS 最长递增子序列

问题描述：找出一个n个数的序列的最长单调递增子序列： 比如A = {5,6,7,1,2,8} 的LIS是5,6,7,8

1. O(n^2)的复杂度：

1.1 最优子结构：
LIS[i] 是以arr[i]为末尾的LIS序列的长度。则：
LIS[i] = {1+Max(LIS(j))}; j<i, arr[j]<arr[i];
LIS[i] = 1, j<i, 但是不存在arr[j]<arr[i];
所以问题转化为计算Max(LIS(j)) 0<i<n

1.2 重叠的子问题：
以arr[i] (1<= i <= n)每个元素结尾的LIS序列的值是 重叠的子问题。
所以填表时候就是建立一个数组DP[i], 记录以arr[i]为序列末尾的LIS长度。

1.3 DP[i]怎么计算？
遍历所有j<i的元素，检查是否DP[j]+1>DP[i] && arr[j]<arry[i] 若是，则可以更新DP[i]

int maxLength = 1, bestEnd = 0;
DP[0] = 1;
prev[0] = -1;

for (int i = 1; i < N; i++)
{
   DP[i] = 1;
   prev[i] = -1;

   for (int j = i - 1; j >= 0; j--)
      if (DP[j] + 1 > DP[i] && array[j] < array[i])
      {
         DP[i] = DP[j] + 1;
         prev[i] = j;
      }

   if (DP[i] > maxLength)
   {
      bestEnd = i;
      maxLength = DP[i];
   }

2. O(nlog)的复杂度

基本思想：

首先通过一个数组MaxV[nMaxLength]来缓存递增子序列LIS的末尾元素最小值；通过nMaxLength 记录到当前遍历为止的最长子序列的长度;

然后我们从第2元素开始，遍历给定的数组arr，
1. arr[i] > MaxV[nMaxLength], 将arr[i]插入到MaxV[++nMaxLength]的末尾 -- 意味着我们找到了一个新的最大LIS
2. arr[i] <= MaxV[nMaxLength], 找到MaxV[]中刚刚大于arr[i]的元素，arr[j].arr[i]替换arr[j]
因为MaxV是一个有序数组，查找过程可以使用log(N)的折半查找。
这样运行时间: n个整数和每个都需要折半查找 -- n*logn = O(nlogn)

• if > 说明j能够放在最长子序列的末尾形成一个新的最长子序列.
• if< 说明j需要替换前面一个刚刚大与array[j]的元素

最后，输出LIS时候，我们会用一个LIS[]数组，这边LIS[i]记录的是以元素arr[i]为结尾的最长序列的长度

---

初始化准备工作：

MaxV[1]首先会被设置成序列第一个元素 即 MaxV[1] = arr[0]，在遍历数组的过程中会不断的更新。
nMaxLength = 1

---

举个栗子：
arr = {2 1 5 3 6 4 8 9 7}

• 首先i=1, 遍历到1， 1 通过跟MaxV[nMaxLength]比较: 1<MaxV[nMaxLength],
  发现1更有潜力（更小的有潜力，更小的替换之）
  1 更有潜力, 那么1就替换MaxV[nMaxLength] 即 MaxV[nMaxLength] =1 ;
  这个时候 MaxV={1}， nMaxlength = 1，LIS[1] = 1;

• 然后 i =2, 遍历到5， 5通过跟MaxV[nMaxLength]比较, 5>MaxV[nMaxLength],
  发现5 更大； 链接到目前得到的LIS尾部；
  这个时候 MaxV={1，5}， nMaxlength++ = 2， MaxV[nMaxLength]=5， LIS[i] = 1+1 = 2;

• 然后 i =3，遍历到3, 3 通过跟MaxV[nMaxLength]比较, 3<MaxV[nMaxLength],
  发现3更有 潜力，然后从 nMaxLength往前比较，找到第一个刚刚比3大元素替换之。（稍后解释什么叫刚刚大）
  这个时候 MaxV={1,3}， nMaxlength = 2; 3只是替换， LIS[i]不变 = LIS[3]= 2;

• 然后 i =4，遍历到6， 6 通过跟 MaxV[nMaxLength]比较, 6>MaxV[nMaxLength],
  发现6更大； 6就应该链接到目前得到的LIS尾部；
  这个时候，MaxV={1,3,6} ，nMaxlength = 3，MaxV[nMaxLength+1]=6 , LIS[4] = 3

• 然后i =5，遍历到4, 4 通过跟MaxV[nMaxLength] = 6比较, 4<MaxV[nMaxLength],
  发现4更有潜力，然后从nMaxLength往前比较，找到刚刚比4大元素 也就是 6替换之。
  这个时候 MaxV={1,3,4}， nMaxlength = 3，4只是替换， LIS[i]不变 = LIS[5]= 3;

• 然后i=6, 遍历到8， 8通过跟MaxV[nMaxLength]比较, 8>MaxV[nMaxLength],
  发现8更大； 8就应该链接到目前得到的LIS尾部；
  这个时候 MaxV={1,3,4,8}， nMaxlength = 4, Maxv[nMaxlength]=8 LIS[6]=4,

• 然后i=7, 遍历到9， 9通过跟MaxV[nMaxLength]比较, 9>MaxV[nMaxLength],
  发现9更大； 9就应该链接到目前得到的LIS尾部；
  这个时候 MaxV={1,3,4,8，9}， nMaxlength = 5, Maxv[nmaxlength]=9, LIS[7] = 5;

• 然后i=8, 遍历到7, 7 通过跟MaxV[nMaxLength] = 9比较, 7<MaxV[nMaxLength],
  发现7更有潜力，然后从nMaxLength往前比较，找到第一个比7大元素 也就是 8替换之。
  这个时候 MaxV={1,3,4,7,9}, nMaxLength = 5, Maxv[nMaxlength]=9
LIS[8] = LIS[替换掉的index] = 4;

--	2	1	5	3	6	4	8	9	7
i	1	2	3	4	5	6	7	8	9
LIS	1	1	2	2	3	3	4	5	4
MaxV	2	1	1,5	1,3	1,3,6	1,3,4	1,3,4,8	1,3,4,8,9	1,3,4,7

java实现：

import java.util.*;

public class LIS {
    public static int lengthofLCS(int[] arr){
        // 辅助变量
        int[] MaxV = new int [arr.length+1]; // 记录递增子序列 LIS 的末尾元素最小值 
        int nMaxLength = 1; // 当前LIS的长度
        int [] LIS = new int[arr.length+1]; //LIS[i]记录的是以第i个元素为结尾的最长序列的长度
        // 初始化
        MaxV[0] = -100;
        MaxV[nMaxLength] = arr[0];
        LIS[0] = 0;LIS[1] = 1;

        for(int i=1;i<arr.length;i++){
            if(arr[i] >MaxV[nMaxLength]){
                MaxV[++nMaxLength] = arr[i];
                LIS[i] = LIS[i-1]+1;
            }
            else{
                // 新元素 更小，更有“潜力”，替换大的元素
                int index = binarySearch(MaxV,arr[i],0,nMaxLength);     
                //*     
                LIS[i] =index;
                MaxV[index] = arr[i];
            }
        }
        Arrays.sort(LIS);
        return LIS[LIS.length-1];
    }
    // 在MaxV数组中查找一个元素刚刚大于arr[i]
    // 返回这个元素的index
    public static int binarySearch(int []arr, int n, int start, int end){
        while(start<end){
            int mid = (start + end)/2;
            if(arr[mid]< n){
                start = mid+1;
            }
            else if(arr[mid]> n) {
                end = mid -1;
            }
            else 
                return mid;
        }
        return end;
    }
    public static void main(String[] args) {
        int[] arr = {2,1,5,3,6,4,8,9,7};
        System.out.println(lengthofLCS(arr));
    }

}

* : MaxV里面的数组下标代表了长度为index的最长子序列末尾元素，反过来就是末尾元素在MaxV里对应的下标就是他子序列的长度

---

可以转化为LCS的问题

• 给一个字符串，求这个字符串最少增加几个字符能变成回文
• 要在一条河的南北两边的各个城市之间造若干座桥．桥两边的城市分别是 a(1)...a(n) 和 b(1)...b(n). 且南边 a(1)...a(n) 是乱序的，北边同理，但是要求 a(i) 只可以和 b(i) 之间造桥, 同时两座桥之间不能交叉. 希望可以得到一个尽量多座桥的方案.

---

以我和蓝盆友的讨论做结：

- 通常DP是一个不算最好，但是比最直接的算法好很多的方法。 DP一般是O（n^2）;但是如果想进一步优化 O（nlogn）就要考虑其他的了

- 对，要想更好的方法就是要挖掘题目本身更加隐匿的性质了