| 姓名 | 具体分工 |
|---|---|
| 叶昊明 | 算法设计与改进,构造测试用例,编写部分程序代码,博客主要内容的撰写 |
| 张鸿霖 | 原型设计与实现,编写主要程序代码,实现各种接口,代码的诸多调试 |
一、原型设计
1. 设计工具:墨刀 (简单易上手,较低的学习成本)
2. 设计说明:
- 我们设计并实现了经典的3×3和4x4的数字华容道问题。
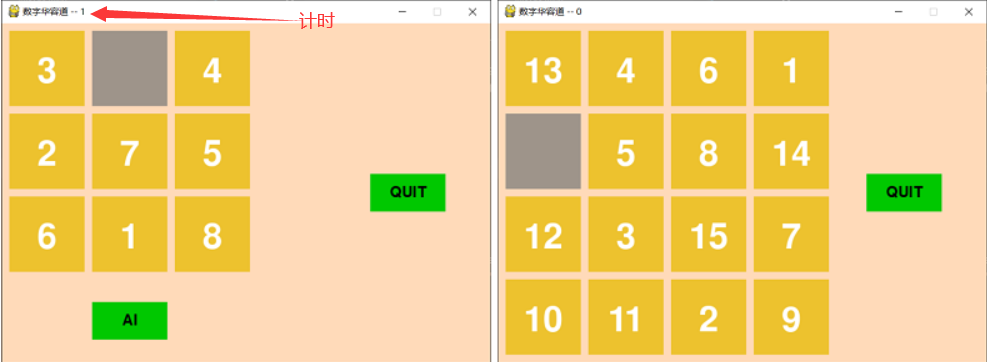
- 在游戏的进行中将会进行计时(在标题栏显示),游戏结束时根据所进行的时间将进行排名。
- 通过键盘进行人机交互来使得空白位置进行移动,移动至目标状态时便可完成游戏(默认右下角挖空),并显示"Time: XXs"字样。
- 游戏过程中如果不知道该如何进行接下来的步骤,可以点击“AI”按钮(此功能仅限3x3),此时计算机将自动进行复原,并逐步展示复原的过程,此次游戏的时间不会计算至排行榜。
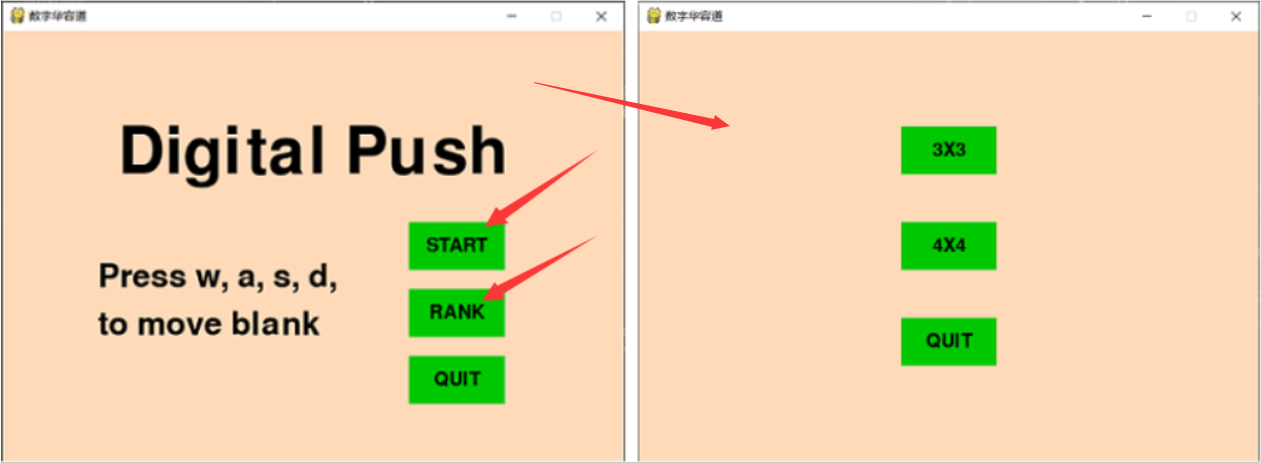
首页:
点击START或RANK进入选择界面
游戏界面:
排行榜和游戏通关界面:

3. 结对过程:
- 因为是室友,当时又坐在一起,自然而然理所当然毅然决然兴味盎然毛骨悚然地结在一个队伍里
- 虽然课程不尽相同,但是课余时间经常相互提起作业内容,如起床时、临睡前等

4. 遇到的困难与解决方法:
- 困难描述:一开始原型的设计思路不是很清晰明确,也基本没使用过什么原型模型设计工具,虽然是室友,但是二人的选课不相一致,课程冲突较大,共同商讨的时间较少。
- 解决尝试:原型的设计经过了漫长的讨论与选定,对于题目的理解也是经历了斟酌的,在商议过程中又结合了题目后续发布的内容才最终确定,原型模型设计工具也参考了其他人的建议。在时间上,我们也常常在深夜进行商讨与分工的完成,平时也会在QQ上积极交流。
- 是否解决:虽然经过了长时间的讨论与,但最终完美地解决了所有问题,结果上来看还是很好的,克服了所有难关。
- 有何收获:二人进行了极大的交流,进行了软件工程所要求的需求分析等关键步骤,也懂得了这些步骤的重要性。原型模型设计上也有了更深入的了解,也懂得了如何使用相关工具。
5. 原型设计实现: 使用Python的pygame库
- 乱序棋盘生成:先生成正确序列,再随机移动1000次,形成乱序。
- 移动算法与生成乱序棋盘的移动算法相同。
def init_load(self):
'''初始化棋盘
以正确序列为基础随机移动一千次
'''
for i in range(self.shape*self.shape): # 生成正确的棋盘序列 self.shape = 棋盘大小
self.tiles.append(str(i+1))
self.goal.append(str(i+1))
for i in range(2): # 生成棋盘边界
mod1 = i*(self.shape-1)+1
mod2 = int(((self.shape-1)/mod1)*self.shape)
for j in range(self.shape):
self.border[i].append(mod1*j)
self.border[i+2].append(mod1*j+mod2)
for count in range(1000): # 随机移动一千次
pos = random.choice(self.pos) # 获取随机移动的方向
spot = self.empty_pos + pos # 移动后空白块的位置
if pos == -self.shape and self.empty_pos not in self.border[0]: # 上移
self.tiles[self.empty_pos], self.tiles[spot] = self.tiles[spot], self.tiles[self.empty_pos]
self.empty_pos = spot
elif pos == -1 and self.empty_pos not in self.border[1]: # 左移
self.tiles[self.empty_pos], self.tiles[spot] = self.tiles[spot], self.tiles[self.empty_pos]
self.empty_pos = spot
elif pos == 1 and self.empty_pos not in self.border[3]: # 右移
self.tiles[self.empty_pos], self.tiles[spot] = self.tiles[spot], self.tiles[self.empty_pos]
self.empty_pos = spot
elif pos == self.shape and self.empty_pos not in self.border[2]: # 下移
self.tiles[self.empty_pos], self.tiles[spot] = self.tiles[spot], self.tiles[self.empty_pos]
self.empty_pos = spot
二、AI与原型设计实现
1. 代码实现思路
网络接口的使用:使用Python的 requests库进行API接口调用
算法基本思路
-
问题转化:
-
先将数字华容道抽象成与排列相关的数学模型,用数0~8表示相应的小块,其中0表示空白,即需要按照一定的移动规则,将打乱的数字复位(在有解的情况下)。
-
原游戏可以用3×3的数组进行表示,但为了便于处理,我们将其一字排开,并使用字符串进行处理(这样可以便于处理游戏中的每个数字的单个状态,也便于处理整个游戏状态,也可以节省空间)。
-
故此时游戏变为在一定规则下进行两个字符串的相互转化。
-
状态是否有解的判定法则(逆序列):
-
将模型转化为字符串后,当我们忽略空白位置时,显而易见这是一个八个数字的排列。如果学习过基础的线性代数就可以很容易地知道,奇排列是指逆序数为奇数的排列,偶排列是指逆序数为偶数的排列,且对调排列中的任意两个数字位置即可将奇排列变位偶排列,或者将偶排列变为奇排列。
-
我们的排列状态转化是有规则的,我们可以发现无论如何腾挪空白的位置,始终相当于将某一个数字单独移动两次(空白上下移动)或零次(空白左右移动),即这样的变化规则是不会改变排列的奇偶性的。
-
由此我们可以得出是否有解的判定法则:若初始状态和目标状态排列的奇偶性相同则有解,否则便是无解。
-
求解过程(非启发式搜索(盲目搜索)bfs+哈希判重,逆推获得步骤):
-
我们先忽略强制交换的要求。因为要求最短路径,bfs便是很好的一个方法,我们将当前空白位置可以移动的状态放入一个队列,并标记好相应的步数,此后当我们搜寻到目标状态时即找到了最短的步数。
-
但是仅仅利用bfs是不可行的,因为会进行很多重复计算,解空间的数量级可达到O(2^n),n为空白移动的步数。此时问题便是如何进行判重并剪枝,康托展开是一个很好的方法,尤其是对于这种全排列问题,虽然它每次都需要计算,但是对于固定长度为9的排列,其计算时间可看做O(1)。但我们使用的是哈希映射(C++可以使用map,python可以使用字典等),每次移动空白位置前的状态记为父结点,其后续可以达到的状态(最多4个,最少2个)记为子结点,每次进行搜索后,都将子结点指向父结点(每个子结点的父结点只有1个,可以唯一标识求解路径),这样处理后,如果对于当前的状态可以找到父结点,即说明已经搜索过了这个结点,并且由于bfs的特性可知,先前搜索过的一定比后续搜索到的解优,故可以进行剪枝。
-
如果当前状态没有父结点,那么便可以继续进行搜索。当我们搜索到了目标状态后,便可以逆推至初始状态结点,进而求解空白位置移动的序列。但是此时需要将空白序列逆序输出。
-
那么如何判断空白位置是进行了哪个方向的移动呢?在状态字符串中可以看到,如果空白向上移动,那么空白位置便向左移动了3个位置,即为“w”,以此类推便可以得到最终的移动步骤序列。
-
当空白位置不是0时,只需要更改空白所对应的数字即可。这可以通过更改相应参数完成。
贴出你认为重要的/有价值的代码片段,并解释
- 图像处理:题目所要求的是图片华容道,并不是数字华容道,所以我们仍需要进行一些预处理,难点在于如何找出乱序图片的目标图片。
- 转换思路:分别将乱序图片与目标图片均分为九块并计算每小块对应的像素均值。通过比对乱序图片小块在目标图片中存在的数量找出目标图片(存在8个即为目标图片)
- 目标图片:由于所给定的图片只有有限多个,因此我们先对目标图片进行预处理并将数据存储为json文件,处理方法如上。每张目标图片的信息对应一个字典,包含以下两个信息
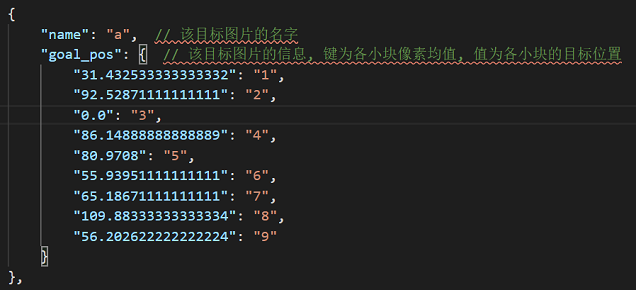
乱序图片处理和寻找目标图片代码:
def crop(im):
'''
将乱序图片切块,并记录每一小块的像素值储存到列表中
并且将每一小块从左上按行从1~9命名保存到temp文件夹下
'''
i = 1
empty_pos = 0 # 空白块的位置
data = [] # 每一小块的像素值,字符串形式
for y in range(3): # 切成9小块并计算每小块的像素均值
for x in range(3):
temp = np.array([0, 0, 0])
croped = im.crop((300*x, 300*y, 300*(x+1), 300*(y+1))) # 切块
croped = croped.resize((150, 150)) # 压缩
r_croped = np.array(croped) # 将图片信息转化为数组
for w in range(150): # 计算像素值
for h in range(150):
temp += r_croped[w][h]
temp = temp/22500
data.append(str(temp[0]))
if (temp == np.array([255., 255., 255.])).all(): # 纯白即为空白块
empty_pos = i # 标记空白块初始位置
croped.save('AI_Competition/temp/'+str(i)+'.jpg')
else:
croped.save('AI_Competition/temp/'+str(i)+'.jpg')
i += 1
return data, empty_pos # 返回乱序图片小块信息, 空白块初始位置
def FindGoalPic(temp_data):
'''
从所有目标图片中找出乱序图片的目标图片的信息。
目标图片的信息组成(一个字典):键为每一小块的像素值,值为每一小块的目标位置。
通过逐一查找乱序图片每一小块的像素值与各目标图片没一小块像素值不相同的小块个数,有且只有一个小块的像素值不一样的图片即为目标图片。
temp_data: 乱序图片9个小块的信息,列表形式
'''
with open('AI_CompetitionGoal_Pic_datasdatas.json', 'r') as f:
goals = json.load(f) # 读入所有目标图片的信息,goals是一个列表
f.close()
for target_data in goals:
count = 0 # 待处理图片与该目标图片不相同小块的数量
for i in range(9):
if temp_data[i] not in target_data['goal_pos']:
count += 1
if count > 1: # 超过1个小块不一样就不是目标图片
break
if count == 1: # 有且仅有一个小块不一样(空白块),就是目标图片
break
return target_data # 返回目标图片的信息
def FindInitPosition(temp_data, target_data):
'''
将乱序图片信息转换成初始位置序列,用字符串表示
temp_data: 乱序图片小块信息
target_data: 目标图片信息
'''
for key in target_data['goal_pos'].keys(): # 找出被挖空的小块
if key not in temp_data:
blanked = key
init_pos = '' # 储存初始位置序列
for i in range(9):
if temp_data[i] in target_data['goal_pos']:
init_pos += target_data['goal_pos'][temp_data[i]]
else:
init_pos += target_data['goal_pos'][blanked]
return init_pos # 返回初始序列
- AI算法
-
预处理:
我们使用了两个数组(类似经典bfs问题中的增量数组)来便于我们的后续处理(若不使用也可,只是代码量会增加)。一维数组dir包含9个元素,每个元素依次代表对应位置空白可移动的方向个数,如在最左上角的空白块只有下和右两个方向可以移动。二维数组dis包含了每个位置上空白可以进行交换的位置,如第一个元素为{1,3},表示空白格在左上角时可以交换的是第1个和第3个位置上的元素(空白格左上角位置记为0)。以此类推,在交换的时候只需要一个循环就可以方便地处理所有交换情况了。 -
核心算法(bfs+哈希判重)代码:
-
def bfs(init_pos, empty, stop_step=100000):
''' 核心算法
通过bfs+哈希判重找出最优解
init_pos: 初始序列
empty: 空白块对应的字符
stop_step: 停机步, 即为发生交换的步数。默认100000, 即不交换。
'''
global step # 当前步数
dir = [2, 3, 2, 3, 4, 3, 2, 3, 2] # 对应位置可移动的方向个数
dis = [[1, 3], [0, 2, 4], [1, 5], [0, 4, 6], # 对应位置可移动到的位置
[1, 3, 5, 7], [2, 4, 8], [3, 7], [4, 6, 8], [5, 7]]
mp = {}
q1 = queue.Queue() # 储存序列信息
q2 = queue.Queue() # 储存步数
q1.put(init_pos)
q2.put(0)
while(not q1.empty()):
father_pos = q1.get()
step = q2.get()
if step == stop_step: # 当前步数等于交换步数, 停止搜索, 返回现在的位置序列和解题步骤
return father_pos, Path_search(mp,init_pos, father_pos,empty)
pos = get_empty_pos(father_pos, empty) # 获取空白块的位置
if father_pos == '123456789': # 达到目标, 输出解题步骤
return init_pos, Path_search(mp,init_pos, father_pos,empty)
for i in range(dir[pos]): # bfs搜索
child_pos = list(father_pos) # 将字符串转化为列表, Python中字符串不可变
child_pos[pos], child_pos[dis[pos][i]] = child_pos[dis[pos][i]], child_pos[pos] # 移动空白
child_pos = ''.join(child_pos) # 转换回字符串, 列表不能作为字典的键
if child_pos not in mp: # 重复标记
mp[child_pos] = father_pos
elif child_pos in mp:
continue
q1.put(child_pos)
q2.put(step+1)
性能分析与改进
这里对强制交换作出说明,根据题目要求,我们还需要在移动了一定步数时进行强制交换,此时可分为如下几种情况(但我们仍然使用之前的bfs+哈希判重策略)
- 初始状态有解,强制交换发生在最优解步数之前:此时是较为特殊又是最简单的一种情况,即相当于未发生强制交换。
- 初始状态有解,强制交换发生在最优解步数之后:
- 理论上的最优解方法:我们使用的算法并不是引导式搜索,一定程度上还属于盲目搜索,所以经过以下策略可以得出最优解,但是时间上的开销将大大增加。
假设在第n步进行强制交换,此时第n步之前一定解出题目,但是由于前n步仍然要进行移动,所以我们可以利用bfs将前n步移动后的所有状态保存在队列中,此后我们对于每一个状态进行如下的决策:如果强制交换后有解,再次以当前状态为初始状态进行bfs求解,此后得到的所有解中,一定有一个最优值(即最小的),选择之即可;如果强制交换后无解,我们可以通过遍历所有可调换的方块进行后续求解(无解状态可以剪枝),此时理论上也可以得到最优解,但计算时间将大大增加。 - 改进后的较优解方法:在(1)中,我们使用了穷举的方式进行求解,虽然理论上可以得到最优解,但计算时间将会比较多,虽然并不是完全NP问题,但所计算时间较长终归是不好的。我们可以使用随机化算法进行如下改进:在强制交换前的所有保存在队列中的状态里,随机选取m个进行计算;在强制交换无解后,在所有可调换的状态中随机选取p个进行计算,此时可以通过调整参数p和m的值进行对算法性能的观测;甚至还可以通过利用评测函数来评估每种状态的优劣,并可利用模拟退火等最优化算法进行求解。但此时的改进,可能需要多次运行才可以得到较优的解,但每次运行所需要的时间将会大大减小。
- 我们实际采用的方法:强制交换前的状态我们只选取其中一种,通过在bfs中设置停机步(数值上即为交换步数)以获取其最后的状态;强制交换后的若有解则再次进行bfs,若无解,则在所有的交换可能中只选取一个(有解的状态),这样所耗费的时间上再次减小,但移动的步数将偏离最优解(甚至偏离较多)。
- 理论上的最优解方法:我们使用的算法并不是引导式搜索,一定程度上还属于盲目搜索,所以经过以下策略可以得出最优解,但是时间上的开销将大大增加。
- 初始状态无解:在强制交换前与强制交换后所采取的策略大体上同2相同,只是编程时有些许细微的小差别。
- 因为强制交换的步数在20以内,所以可以不考虑一种极端情况,如:初始状态无解,强制交换发生在第100步。
展示性能分析图和程序中消耗最大的函数
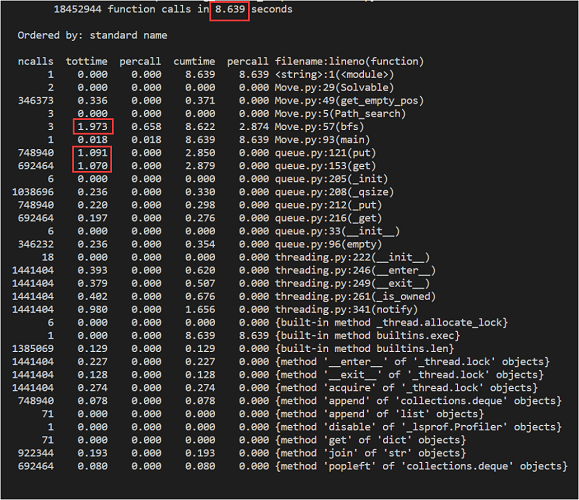
由性能分析图可以看出, 消耗最大的函数是bfs和哈希的判重函数。
图片的处理由于预先处理了目标图片的数据,因此没有多大的消耗
展示出项目部分单元测试代码,并说明测试的函数,构造测试数据的思路
测试数据构造思路:初始状态有解,交换步骤在解之后;初始状态有解,交换步骤在解之前;初始状态无解各3种,最后随机一种
import unittest
from BeautifulReport import BeautifulReport
import Move
class TestFunction(unittest.TestCase):
@classmethod
def setUp(self):
print("开始测试")
@classmethod
def tearDown(self):
print("测试结束")
def test_after_1(self):
print('初始状态有解,交换步骤在解之后')
print('初始序列: %s, 空白格: %s, 在第%d步交换, 交换%d, %d' % ('123459786', '9', 20, 1, 2))
path, Myswap = Move.main('123459786', '9', 20, [1,2])
print('最优解路径: ', path)
print('自由交换位置: ',Myswap)
def test_after_2(self):
print('初始状态有解,交换步骤在解之后')
print('初始序列: %s, 空白格: %s, 在第%d步交换, 交换%d, %d' % ('129453786', '9', 20, 7, 8))
path, Myswap = Move.main('129453786', '9', 20, [7,8])
print('最优解路径: ', path)
print('自由交换位置: ',Myswap)
def test_before_1(self):
print('初始状态有解,交换步骤在解之前')
print('初始序列: %s, 空白格: %s, 在第%d步交换, 交换%d, %d' % ('278641539', '9', 5, 5, 9))
path, Myswap = Move.main('278641539', '9', 5, [5,9])
print('最优解路径: ', path)
print('自由交换位置: ',Myswap)
def test_before_2(self):
print('初始状态有解,交换步骤在解之前')
print('初始序列: %s, 空白格: %s, 在第%d步交换, 交换%d, %d' % ('279648531', '9', 3, 1, 9))
path, Myswap = Move.main('279648531', '9', 3, [1,9])
print('最优解路径: ', path)
print('自由交换位置: ',Myswap)
def test_not_1(self):
print('初始状态无解')
print('初始序列: %s, 空白格: %s, 在第%d步交换, 交换%d, %d' % ('728641539', '9', 5, 3, 7))
path, Myswap = Move.main('728641539', '9', 5, [3,7])
print('最优解路径: ', path)
print('自由交换位置: ',Myswap)
def test_not_2(self):
print('初始状态无解')
print('初始序列: %s, 空白格: %s, 在第%d步交换, 交换%d, %d' % ('729648531', '9', 7, 3, 1))
path, Myswap = Move.main('728641539', '9', 5, [3,1])
print('最优解路径: ', path)
print('自由交换位置: ',Myswap)
def test_4(self):
print('随机')
print('初始序列: %s, 空白格: %s, 在第%d步交换, 交换%d, %d' % ('123456789', '5', 0, 1, 9))
path, Myswap = Move.main('123456789', '5', 0, [1,9])
print('最优解路径: ', path)
print('自由交换位置: ',Myswap)
if __name__ == "__main__":
suite = unittest.TestSuite()
tests = [
TestFunction('test_after_1'),
TestFunction('test_after_2'),
TestFunction('test_before_1'),
TestFunction('test_before_2'),
TestFunction('test_not_1'),
TestFunction('test_not_2'),
TestFunction('test_4'),
]
suite.addTests(tests)
BeautifulReport(suite).report(filename='AI_Competition/TestReport.html',
description='测试报告',
log_path='.')
2. 贴出Github的代码签入记录,合理记录commit信息。
3. 遇到的代码模块异常或结对困难及解决方法。
- 困难描述:虽然二人之前有过些游戏编程的经验,但是是使用的比较基础的C语言,并未利用已有的库函数。此次使用的是python语言,尤其是pygame模块二人均从未使用过,需要从零开始;此外,游戏中的AI算法实现也需要一定的考究,不仅仅是做出游戏这么简单,时间紧迫,任务繁重。
- 解决尝试:一人主要负责实现AI算法并进行代码的调试与结果的测试,另一人主要学习了pygame的使用、图片的处理、键盘交互与UI设计。在此期间,二人也积极地交流、相互加油打气鼓励,并相互督促,同时也在彼此的内容实现中出谋划策,共同测试结果。
- 是否解决:虽然大体上算是从零开始,工作量也不小,但是最终还是解决了问题。遇到的许多细节上的零碎小问题也都相互探讨逐一解决,AI的算法部分完美解决,并成功地应用到了游戏中;交互过程也顺利完成,很好地学习使用了pygame的使用。
- 有何收获:代码能力的锻炼是十分显然的,算法能力也得到了锻炼与加强,相互的合作能力也得到了锻炼。python语言的使用更加熟练,也体验到了python语言的十足魅力。设计出的小游戏也是令人兴奋的,再加上原型的设计等过程,虽然付出了不少的汗水,但最终也让我们都获得了一次前所未有的愉快体验。
4. 评价你的队友。
叶昊明评价张鸿霖:
- 值得学习的地方:兢兢业业,勤勤恳恳的小码农,代码实现效率高、语言转换得很好,命名规范。
- 需要改进的地方:仍需要在代码的实现细节上稍加注意,尤其像消耗答题次数这样的情况下,应该谨慎些再去使用循环跑题目。需要在算法上多下些功夫。
张鸿霖评价叶昊明:
- 值得学习的地方:算法思路清晰实现方便,思维转换很灵敏,能够想到各种方法解决问题,文字编辑能力比较强。
- 需要改进的地方:需要多些编程练习,python的实现上仍需要再熟练些,接口部分不应该放在较晚的时间去完成。还需要再多了解和使用github。
5.PSP表格和学习进度条(二人汇总)
- 学习进度条
| 第N周 | 新增代码(行) | 累计代码(行) | 本周学习耗时(小时) | 累计学习耗时(小时) | 重要成长 |
|---|---|---|---|---|---|
| 1 | 106 | 106 | 12 | 12 | 熟悉了python对图片处理,了解了原型设计工具 |
| 2 | 108 | 214 | 16 | 28 | 熟悉了python中pygame模块的使用与网络接口的使用 |
| 3 | 125 | 339 | 12 | 40 | 成功实现了bfs与哈希判重相结合的算法,构造了测试用例并检验 |
| 3 | 237 | 576 | 20 | 60 | 将所学习与使用的各个模块全部衔接起来,包括图片预处理的部分与算法的结合等 |
- PSP表格
| PSP2.1 | 任务内容 | 计划完成需要的时间(min) | 实际完成需要的时间(min) |
|---|---|---|---|
| Planning | 计划 | 45 | 40 |
| Estimate | 估计这个任务需要多少时间,并规划大致工作步骤 | 30 | 20 |
| Development | 开发 | 1000 | 1300 |
| Analysis | 需求分析 (包括学习新技术) | 60 | 90 |
| Design Spec | 生成设计文档 | 30 | - |
| Design Review | 设计复审 (和同事审核设计文档) | 10 | - |
| Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 40 | 40 |
| Design | 具体设计 | 60 | 80 |
| Coding | 具体编码 | 400 | 500 |
| Code Review | 代码复审 | 30 | 30 |
| test | 测试(自我测试,修改代码,提交修改) | 350 | 500 |
| Reporting | 报告 | 420 | 480 |
| Test Report | 测试报告 | 360 | 370 |
| Size Measurement | 计算工作量 | 30 | - |
| Postmortem & Process Improvement Plan | 事后总结 ,并提出过程改进计划 | 60 | 80 |
| Summary | 合计 | 1465 | 1820 |