2-sat学习笔记

2- sat 问题

序

我笑笑，np完全，弹指一挥间罢了

正文

定义

2-SAT就是2判定性问题，是一种特殊的逻辑判定问题。

我们先来看看什么2-sat,问题，他大概可以理解为，给你一堆bool型变量，每个变量可能为真或假，现在有一种限制关系指

假如(xi)变量选了什么，(yi)只能是什么。我们称变量只有两种可能性的叫2-sat问题，而3-sat或更高的sat不行，因为他们是NP完全的。

我们通过建图来操作2-sat问题

我们来看一个实际的题来说明

eg和平委员会

有n个组，第i个组里有两个节点Ai, Ai' 。需要从每个组中选出一个。而某些点不可以同时选出（称之为不相容）。任务是保证选出的n个点都能两两相容

我们连边的原则是

假设我们有一个关系，选了x不能y，那么选了x是y那一列只能选y'，而选y了则x那一列只能选x'

于是我们就从建两条边，x->y'，y->x'

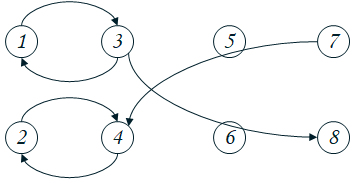
我们的如图，看起来很对称，于是我们的箭头关系是选了u就要选v，于是我们进行缩点，对于之后的图做拓扑序，每一个对应中，选拓扑序前的

于是我们，有了一版代码。。。

在这里注意要做一个，强连通分量中的对应关系

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int Maxm=50000,Maxn=16008;
struct Node{
	int fr,to,lac;
}edge[Maxm],vedge[Maxm];
int vcnt,vh[Maxn],num,col[Maxn],p[Maxn],x,y,cnt,n,m,dfn[Maxn],low[Maxn],dep,sta[Maxn],top,h[Maxn],b[Maxn],a[Maxn];
bool fsta[Maxn],f,flag[Maxn];
void insert(int x,int y){//表示x,y互相仇视 
	int u=(y^1);
	edge[cnt].to=u;
	edge[cnt].fr=x;
	edge[cnt].lac=h[x];
	h[x]=cnt++;
	u=(x^1);
	edge[cnt].to=u;
	edge[cnt].fr=y;
	edge[cnt].lac=h[y];
	h[y]=cnt++;
}
void tarjan(int u){
	dfn[u]=low[u]=++dep;
	fsta[u]=1;sta[++top]=u;
	for(int i=h[u];i!=-1;i=edge[i].lac){
		int to=edge[i].to;
		if(dfn[to]){
			if(fsta[to]) low[u]=min(low[u],dfn[to]);
			continue;
		}
		tarjan(to);
		low[u]=min(low[u],low[to]);
	}
	if(low[u]==dfn[u]){
		num++;
		while(fsta[u]){
			fsta[sta[top]]=0;
			col[sta[top]]=num;
			top--;
		}
	}
}
void vinsert(int x,int y){
	vedge[vcnt].fr=x;
	vedge[vcnt].to=y;
	vedge[vcnt].lac=vh[x];
	vh[x]=vcnt++;
}
int main(){
//	freopen("sp.in","r",stdin);
	scanf("%d%d",&n,&m);
	memset(h,-1,sizeof h);
	for(int i=1;i<=m;i++){
		scanf("%d%d",&x,&y);
		insert(--x,--y);
	}
	for(int i=0;i<2*n;i++) if(!dfn[i]) tarjan(i);
	for(int i=0;i<2*n;i+=2)
		if(col[i]==col[i^1]){
			printf("NIE");//判断无解 
			return 0;
		}
	for(int i=0;i<2*n;i++) p[col[i]]=col[i^1];//求其对应 
	memset(vh,-1,sizeof vh);
	for(int i=0;i<cnt;i++){
		if(col[edge[i].fr]!=col[edge[i].to]){
			vinsert(col[edge[i].to],col[edge[i].fr]);
			b[col[edge[i].fr]]++;
		}
	}
	int ans=0;
//	朴素 
	/*for(int k=1;k<=num/2;k++){
		int v=-1;
		for(int i=1;i<=num;i++){
			if(b[i]==0&&!flag[i]){
				v=i;
				break;
			}
		}
		if(v==-1) break;
		flag[v]=1;
		flag[p[v]]=1;
		for(int i=0;i<2*n;i++){
			if(col[i]==v){
				a[++ans]=i;
			}
		}
		for(int i=vh[v];i!=-1;i=vedge[i].lac)
			b[vedge[i].to]--; 
	}
	*/ 
	queue<int> q1;
	for(int i=1;i<=num;i++) if(b[i]==0) q1.push(i);
	while(!q1.empty()){
		int v=q1.front();
		q1.pop();
		if(!flag[v]){
			for(int i=0;i<2*n;i++){
				if(col[i]==v){
					a[++ans]=i;
				}
			}
			for(int i=vh[v];i!=-1;i=vedge[i].lac){
				b[vedge[i].to]--; 
				if(b[vedge[i].to]==0) q1.push(vedge[i].to);
			}
		}
		flag[v]=1;
		flag[p[v]]=1;
	}
	sort(a+1,a+n+1);
	for(int i=1;i<=ans;i++){
		printf("%d
",a[i]+1);
	} 
	return 0;
}

这是朴素的(n^2)拓扑，我们考虑优化它，可以用队列，这里就不贴代码了，

事实上，我们在进行tarjan是其实相当与做了topo,我们考虑下面的输入

2 2
1 3
1 4

这样能看出.事实上i是可以指向i'的而对于tarjan我们i'的col一定比i的col小

所以我们考虑输出i和i'中小的那个

有

for(int i=0;i<2*n;i+=2){
	f(col[i]<col[i^1]) printf("%d
",i+1);
	else printf("%d
",i+2);
}

好了就这样吧，后面我会补充满汉这个题的。 于2020.2.6 0:41

eg JSOI 满汉全席

这题，水呀。。。。。裸的2-sat

但是要注意存在输出GOOD。。。太坑了

就这样吧，没甚么好说的

我有可能后面补一下塔防，BJOI的，但是
看时间吧，毕竟假期不多了

嵬

2-sat,不过是两个星期六

我困了，两周之内做第二版