选择树
-
概念:假设有k个已经排序的序列,并且想要将其合并成一个单独的排序序列。每个排好序的序列叫走一个
归并段。 -
暴力算法:假设总共有n个数字,每次取k个归并串最小或者最大的一个数,比较k-1次得到所有数中最大或者最小的树,存入新空间中,接着一直这样比较...需要比较的次数是n*(k-1)
-
选择树算法:可以构造完全二叉树的数组表示法。初始状态如下:
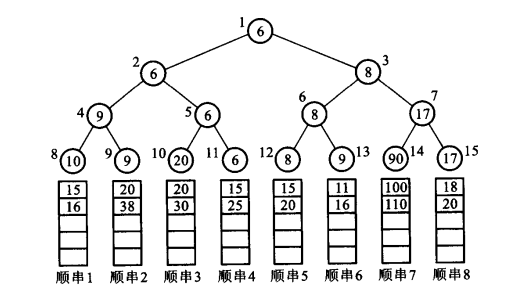
接着将上图最小的6放到新序列中,然后用15替换最下层的6,再进行规范化,接着选出最小,如下:
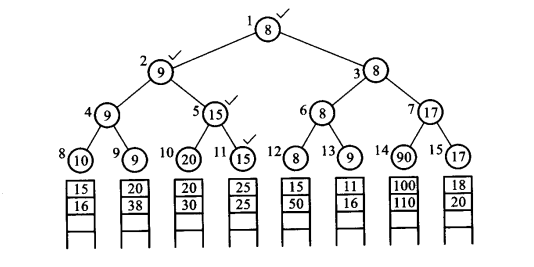
可以看到,每次的比较次数是O(logk),时间复杂度是O(nlogk)
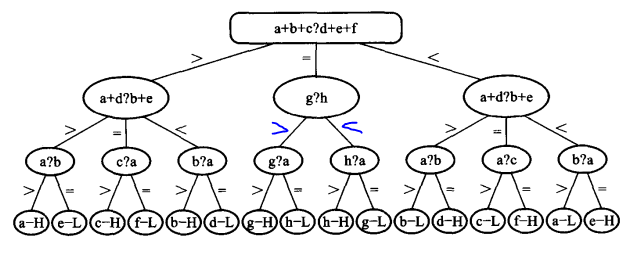
判定树
- 概念:以著名的
8枚硬币的问题进行说明。假定有8枚硬币a-h,其中一枚硬币是伪造的。伪造的硬币可能比标准的重或者轻,所以可能的结果有16种情况。
-
如图,无论是什么情况,经过3次比较一定出结果
-
代码如下:
char Compare(int a, int b)
{
if(a > b)
return '>';
else if(a < b)
return '<';
else
return '=';
}
void comp(int x,int y,int z)
{
if(x>z)
cout << x << "heavy";
else
cout << y << "light";
}
void eightcoins()
{
int a,b,c,d,e,f,g,h;
cin >> a >> b >> ... >> h;
switch(Compare(a+b+c,d+e+f)) {
case '=':
if(g>h)
comp(g,h,a)
else
comp(h,g,a);
break;
case '>':
switch(Compare(a+d,b+e)) {
case '=':
comp(c,f,a);
break;
case '>':
comp(a,e,b);
break;
case '<':
comp(b,d,a);
break;
}
break;
case '<':
switch(Compare(a+d,b+e)) {
case '=':
comp(f,c,a);
break;
case '>':
comp(d,b,a);
break;
case '<':
comp(e,a,b);
break;
}
break;
}
}
查找树
一般来说,查找树指的是二叉查找树,其查找过程是从根结点一直向下查找,时间复杂度为O(logn)。
对查找二叉树进行中序遍历,是个递增序列
定义如下:
- 若它的左子树不空,则其左子树上任意结点的关键字的值都小于根结点关键字的值
- 若右子树不空,则其右子树上任意结点的关键字的值都大于根结点的关键字的值
- 它的左右子树又是一个二叉查找树
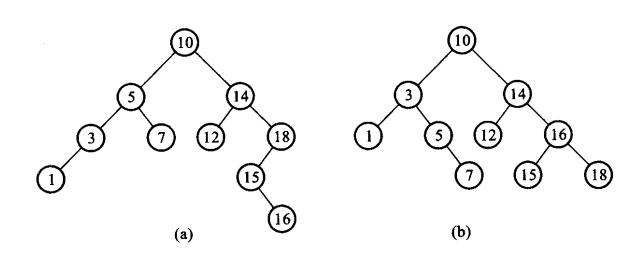
代码实现:
- 定义数据结构:
struct celltype{
records data;
celltype *lchild, *rchild;
};
typedef celltype *BST;- 插入数据:
void Insert(records R, BST &F)
{
if(F == NULL) {
F = new celltype;
F->data = R;
F->lchild = NULL;
F->rchild = NULL;
} else if(R.key < F->data.key)
Insert(R,F->lchild);
else if(R.key > F->data.key)
Insert(R,F->rchild);
}
- 删除数据:
//删除关键字最小的结点并且返回其数据
records DeleteMin(BST & F)
{
records tmp;
BST P;
if(F->lchild == NULL) {
P = F;
tmp = F->data;
F = F->rchild;
delete P;
return tmp;
} else
return DeleteMin(F->lchild);
}
void Delete(keytype k,BST &F)
{
if(F) {
if(k < F->data.key)
Delete(k,F->lchild);
else if(k > F->data.key)
Delete(k,F->rchild);
else
//查找成功
{
if(F->lchild == NULL)
F = F->rchild;
else if(F->rchild == NULL)
F = F->lchild;
else
F->data = DeleteMin(F->rchild);
}
}
}- 查找数据
BST Serach(keytype k,BST F)
{
if(F == NULL)
return NULL;
else if( k == F->data.key)
return F;
else if(k < F->data.key)
return Search(k,F->lchild);
else if(k > F->data.key)
return Search(k,F->rchild);
}