https://codeforces.com/blog/entry/81565
转自codeforces
1392F - Omkar and Landslide
TL;DR: We can show that in the resulting array, every pair of adjacent elements differs by exactly 1 except that there may be at most one pair of adjacent equal elements. It is easy to see that there is only one such array satisfying that condition that also has the same length and sum as the given array, so we simply calculate that array based on the sum of the given array.
我们可以证明,在结果数组中,每一对相邻的元素的差值均为1,或者最多有一组相邻的元素相等。显然只有一个数组满足 和给出的数组具有相同的长度和元素和,所以我们只需要用给出的数组的元素和作为基础来计算结果数组。
Proof: Clearly, the order in which we perform the slides (transfers of one square meter of dirt from aj+1 to aj for some j) does not matter. Consider then performing slides in the following manner: whenever we perform a slide from aj to aj−1, after that slide, if it is possible to perform a slide from aj−1 to aj−2, we will do so, and then from aj−2 to aj−3 and so on. We will call this action "performing a sequence of slides from aj".
证明:显然,我们模拟滑落(把aj+1处的1立方米的土移到aj处)的方式(顺序),不影响最终结果。考虑用下面的方式模拟滑落操作:如果在执行完aj到aj-1的滑落操作后,还能执行aj-1 到 aj-2的滑落操作,我们就继续执行,然后是aj-2到aj-3...。我们将这种操作称为 “ 执行从aj开始的一系列滑落操作 ”
Assume that we have just performed a sequence of slides from aj. We can see that if there was a pair of adjacent elements to the left of aj that were equal, i. e. some k<j such that ak−1=ak, then, assuming that ak−1,ak is the rightmost such pair, then the sequence of slides that we started will end with ak being increased. In this case, ak−1 and ak are no longer equal, but ak,ak+1 may now be equal, so the amount of pairs of adjacent equal elements to the left of aj has either decreased or stayed the same.
假设我们刚刚执行完一次 “ 从aj开始的一系列滑落操作”。我们可以发现,如果(在执行操作前),在aj左侧有一对相邻元素是相等的,设该对元素为ak-1 = ak,k<j。然后假设ak 和 ak+1 是 aj 左侧最靠右边的相等元素,那么我们本次的 "一系列滑落操作" 会以 ak 增加作为结束。在这种情况下,ak-1 和 ak 不再相等,但是 ak, ak+1 现在或许是相等的,所以 aj 左侧的相等元素的对数要么不变,要么减少。
On the other hand, if there was no such pair, then the sequence of slides would end with a1 being increased, meaning it might now be true that a1 and a2 are equal, so that the amount of pairs of adjacent equal elements to the left of aj is either still 0 or now 1.
另一方面,如果在执行操作前没有这种(相邻且相等)元素对,那么 “一系列滑落操作” 会以 a1 增加结束,这意味着现在 a1 和 a2 或许是相等的,所以 aj 左侧的相邻且相等元素的对数是0(保持不变)或者变成了 1。
Combining these two facts, we see that if there were either 0 or 1 pairs of adjacent equal elements to the left of aj to start with, then there will only be either 0 or 1 pairs of adjacent equal elements to the left of aj after performing a sequence of slides from aj.
将这两种结论组合起来,我们会发现如果在一开始, aj 左侧的相邻相等元素的对数是 0 或 1 时,那么在执行从 aj 开始的 “一系列滑落操作后”, aj 左侧的相邻相等元素的对数也只会是 0 或 1 。
Noting that as our array is initially strictly increasing, there are initially no pairs of adjacent equal elements, we can simply first perform as many sequences of slides from a2 as possible, then perform as many sequences of slides from a3 as possible, and so on, until we perform as many sequences of slides from an as possible. When we are performing sequences of slides from aj, there can clearly only be either 0 or 1 pairs of adjacent equal elements to the left of aj, and there can't be any such pairs to the right of aj as that part of the array hasn't been touched yet and is therefore still strictly increasing. Therefore, we can conclude that once all possible slides have been performed, the entire array will contain at most 1 pair of adjacent equal elements.
请注意我们的数组在一开始是严格单调递增的,没有任何一对相邻相等元素,我们只需要先从 a2 开始尽可能多地执行 “一系列的滑落操作”, 然后是 a3 ... ,直到 an。当我们执行从 aj 开始的 “一系列的滑落操作”, 在 aj 的左侧,显然只会有 0 或 1 对相邻相等元素,并且在 aj 的右侧,没有执行过 “一系列的滑落操作”的部分(即保持初始状态的部分)还是严格单调递增的(即没有相邻相等元素对)。综上,我们可以得出结论:在所有的可能的 “一系列的滑落操作” 被执行后,剩余的数组至多含有 1 对相邻相等元素。
Since it cannot be possible to perform any more slides once all possible slides have been performed, all pairs of adjacent elements that are not equal must differ by at most 1. It is easy to see that there is only one array satisfying these conditions that has the same length n and sum S=∑nj=1aj. You can construct this array by starting with the array 0,1,2,…,n−1, then adding 1 to each element from left to right, looping back to the beginning when you reach the end, until the sum of the array is S. From this construction we can derive the following formula for the array:
aj=j−1+⌊S−n(n−1)/2n⌋+{j≤(S−n(n−1)/2)%n}
where {C} is 1 if the condition C is satisfied, and 0 otherwise.
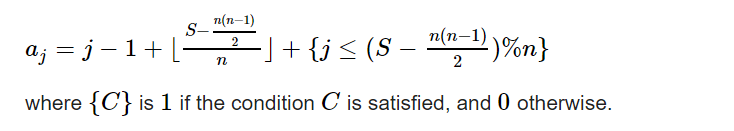
因为在执行所有可行的 操作 后不可能还能执行 操作 , 所有相邻的元素对之间的差值最多为1,显然只有一个元素和为sum且长度相等的数组满足这一条件。你可以从 {0,1,...,n-1} 开始构造这个数组,然后从左到右依次给这个数组每个元素 +1, 重复这一操作,直到数组元素之和等于给出的初始数组,根据这个构造过程我们可以得出下面的公式
。。。。。
C 为真时 {C} 的值为1, 否则为0.