单个定量变量的直方图表示
大家知道,定量变量是连续型变量,即不会像分类变量那样有明显的分类,那么如何将其画成直方图呢?一般来说,会将其按照某个维度来将其分组(group),举个例子。
我们有15个学生的考试成绩:88, 48, 60, 51, 57, 85, 69, 75, 97, 72, 71, 79, 65, 63, 73
如果要画成直方图,X轴是成绩,Y轴是对应的人数,那么X轴可以考虑按“每10分”作为一个group,即[0, 10), [10, 20), [20, 30), ... ,[80, 90), [90, 100)这样组织:
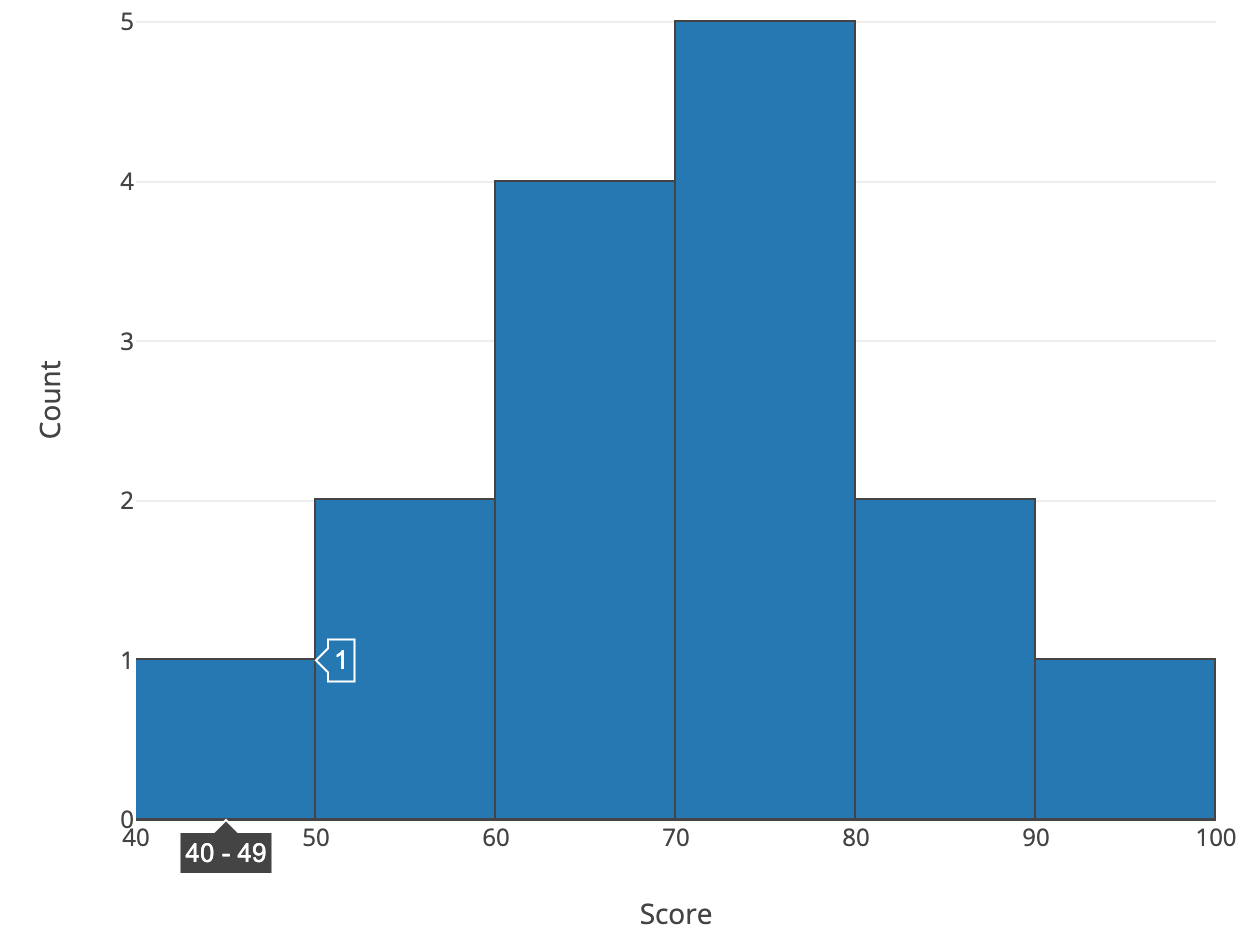
类似分类变量的柱状图,定量变量的直方图的Y轴,也可以将值(value)转换为百分比(percent)
直方图有几个重要的概念是需要掌握的,分别是:shape、center、spread、outliers
shape
shape指从直方图的整体形状来定性其分布特点,一般分为两个维度:
- 对称(Symmetry)/有偏(skewness)
- 有峰(Peakedness)/平滑 (modality)
下面分别举几个例子:

上面的直方图,首先是对称的(即Y轴左右基本对称),其次是有峰的(x=10左右的位置有个单峰值),所以是“对称、单峰值分布”

上面的直方图,也是对称的,而且是有双峰的,所以是“对称、双峰值分布”

上面的直方图,没有明显的峰值,所以是“对称、平滑分布”
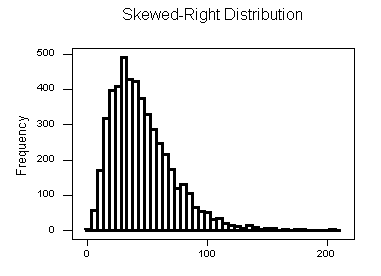
上面的直方图,可以看到右边有很长的长尾数据,所以是“有偏(右偏)、单峰值分布”
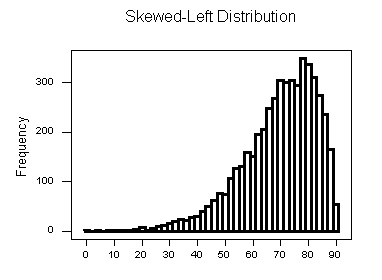
类似地,上面的直方图是“左偏、单峰值分布”
这里可能有个疑惑:为啥峰值偏左的叫右偏,而峰值偏右的叫左偏呢?实际上,这里是根据均值和中位数的相对位置来命名左或右的,下面说完center后会重新提到。
center
直方图的中心可以有很多种定义方法:
- mode:即众数,是X轴上Y值最大的那一个group(即直方图上峰值最高的那一个柱子的值)
- mean:即(加权)平均值,将所有值加权相加后除以总数
- median:即中位数,即将所有样本排序后,所有样本的总数除以2,取中间的1个样本的值(总样本是奇数)或2个样本的值的平均数(总样本是偶数)
举个例子:
我们有15个学生的考试成绩:88, 48, 60, 51, 57, 85, 69, 75, 97, 72, 71, 79, 65, 63, 73
如果按照每10分 来划分group,则直方图为:
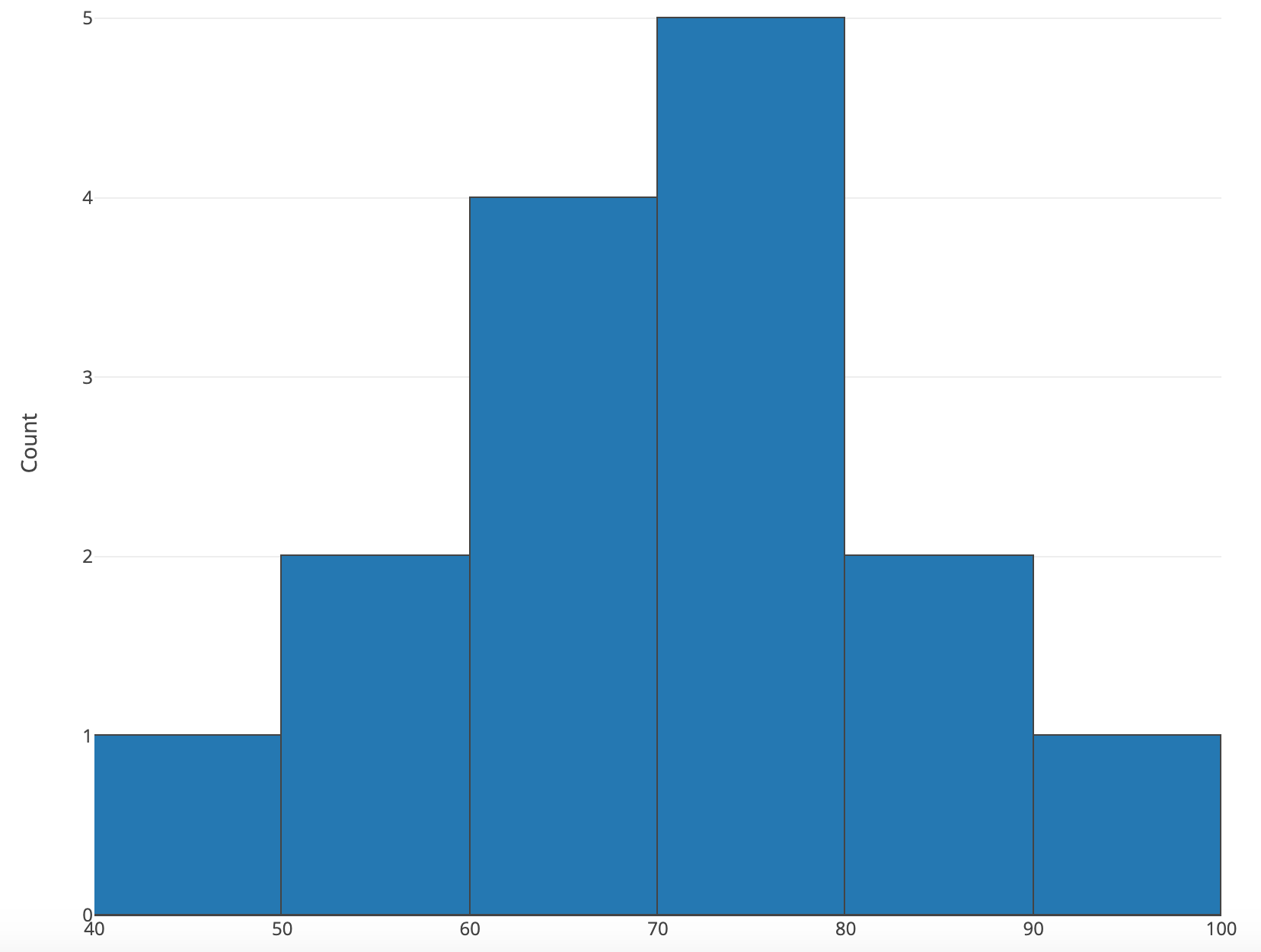
对应上图:
mode:是峰值最高的那个柱子,就是[70, 80)对应的那个柱子的值:5
mean:(88 + 48 + 60 + 51 + 57 + 85 + 69 + 75 + 97 + 72 + 71 + 79 + 65 + 63 + 73) / 15 = 70.2
median:先排序(48, 51, 57, 60, 63, 65, 69, 71, 72, 73, 75, 79, 85, 88, 97),找到中间的值:71
spread
上面提到过,左偏和有偏的问题,这里结合mean和median再进一步阐述下:
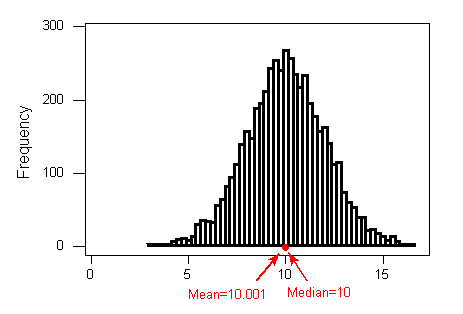
上图是一个对称分布的情况,可见:mean和median基本在一个位置上
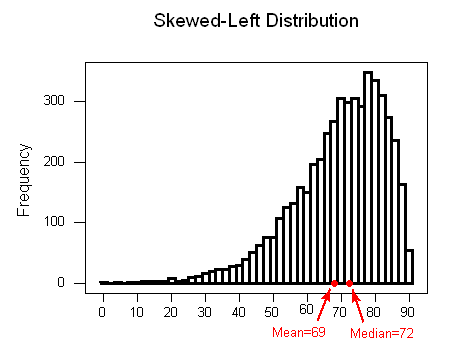
上图是一个左偏的情况,可以看到左侧有很多长尾数据,median受到了长尾数据影响,并没有出现在最高峰值附近而是向左偏移了一点点,但是平均值mean受长尾数据影响更大,其向左偏移的幅度也更大,所以相对对称分布来说,上图中mean和median都向左发生了偏移,所以这种分布叫左偏。
右偏相反理解即可
outliers
即异常值,比如下图:

最右边的值看起来很奇怪,和大部分值都不一样,所以可能会被怀疑为异常值。
一般来说,发现有异常值的时候,需要进一步分析一下其产生的原因,如果是合理的,那么需要保留;如果是不合理的,则需要过滤掉;如果是错误导致的,则需要重新计算。
mode不受异常值影响;median对异常值不敏感;而mean对异常值非常敏感!