STL--关系型容器
1.树的基本概念
1.1二叉搜索树
二叉搜索树:它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
1.2平衡二叉搜索树
平衡二叉搜索树:能够维持根节点的左右子树相对平衡。
例如:AVL-tree、RB-tree、AA-tree。
1.3 AVL tree
AVL tree 是一个加了“额外平衡条件”的二叉搜索树。其平衡条件的建立是为了确保整棵树的深度为O(logN)。直观上的最佳平衡条件是每个节点的左右子树有着相同的高度或者相差1。
1.4 单旋转(single rotation)
插入点位于X的左子树的左节点上—左左,插入点位于X的右子树的右节点上—右右将破坏AVL tree的平衡条件。
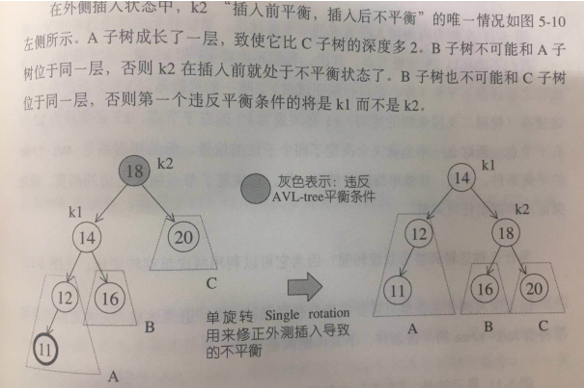
可以利用单旋转来恢复二叉树平衡。K2旋转下去成为k1的右子树。16上提。
1.5 双旋转(Double rotation)
插入点位于X的左子树的右节点上—左右,插入点位于X的右子树的左节点上—右左将破坏AVL tree的平衡条件。利用单旋转无法恢复平衡状态。双旋转可由两次单旋转合并而成。s
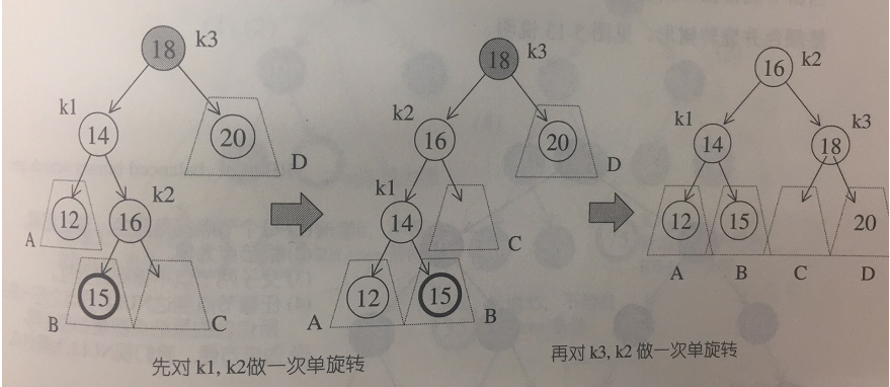
2. RB-tree
RB-tree 是另外一个颇具历史并被广泛运用的平衡二叉搜索树。而且还满足如下条件:
- 每个节点不是红色就是黑色。
- 根节点为黑色。
- 如果节点为红色,其子节点必须是黑色。
- 任一节点至NULL(树尾端)的任何路径所含之黑色节点数必须相同。
根据条件4,新增节点必须为红色,根据条件3,新增节点之父节点必须为红色。当新增节点根据二叉搜索树的规则到达其插入点,却未能符合上述条件时,就必须调整颜色并旋转树形。

2.1 插入节点
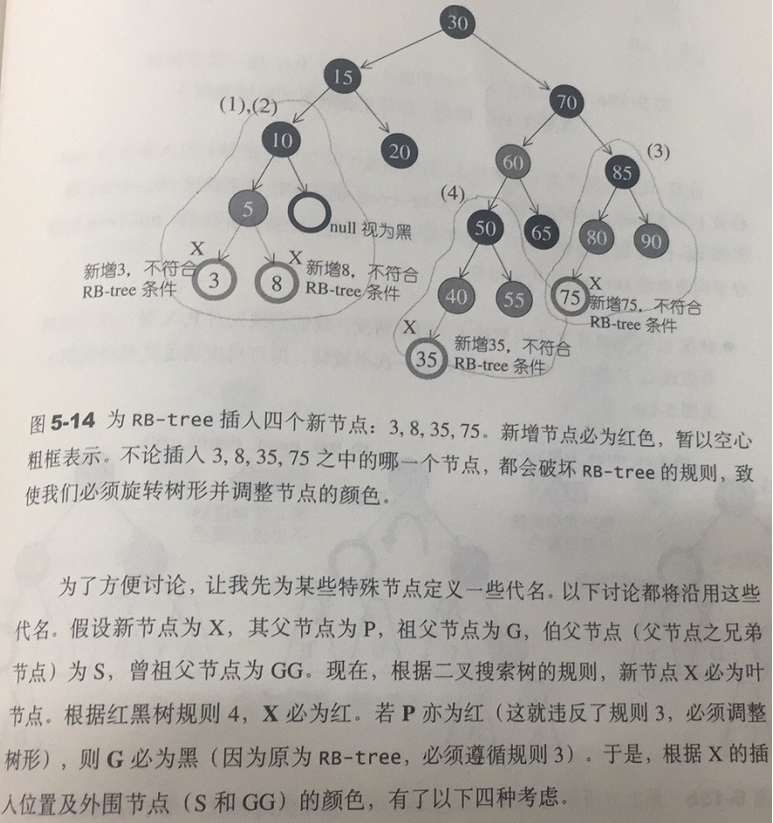
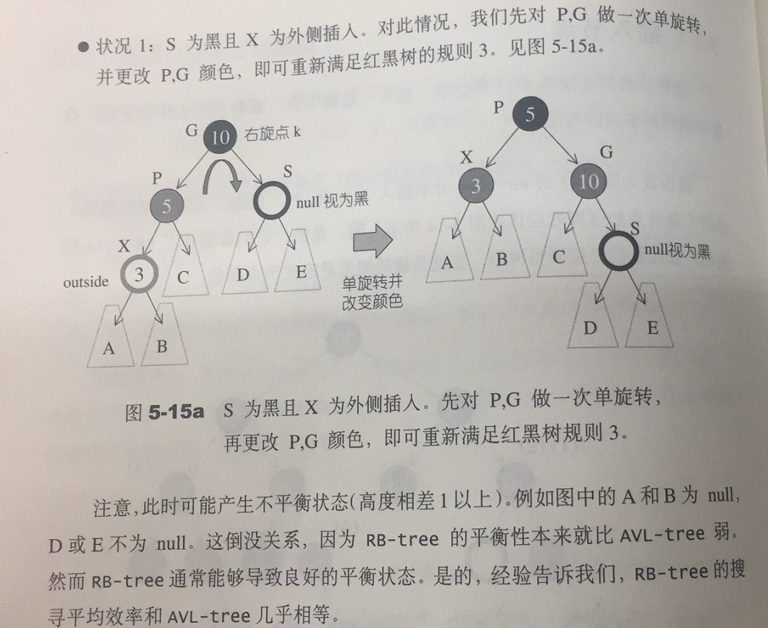
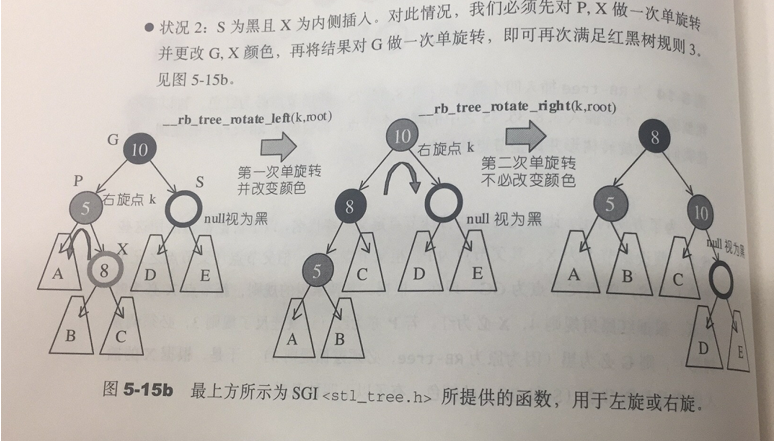
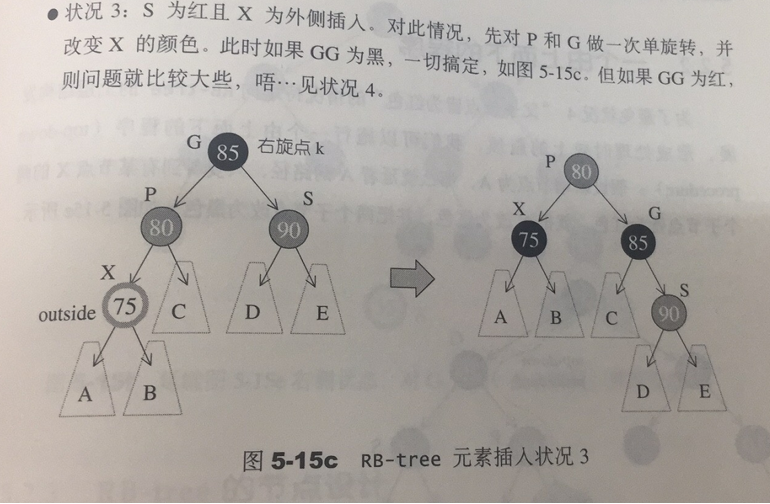
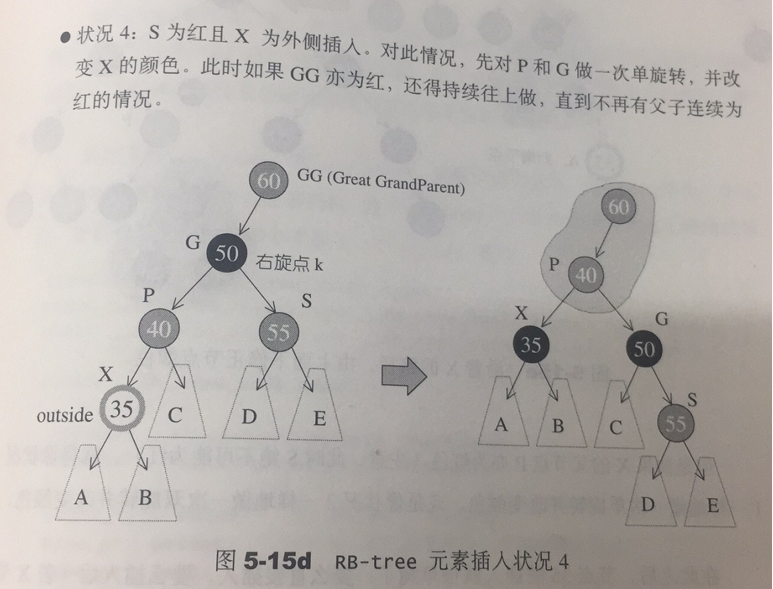
RB-tree的构造与内存管理
构造方式有两种:
1、 用现有的RB-tree复制构造一个新的RB-tree,另一种是产生一颗空空如也的树。
rb_tree<int, int, identity<int>, less<int>> itree;
这行程序代码分别指定了节点的键值、实值、大小比较标准…,然后调用RB-tree的default constructor:
rb_tree(const Compare& comp = Compare())
:node_count(0), key_compare(comp){ init(); }
其中的init()是实际技巧上的一个关键点:
private:
void init(){
header = get_node(); //产生一个节点空间,令header指向它
color(header) = _rb_tree_red; //令header为红色,用来区分header和root(在//iterator.operator++中)
root() = 0;
leftmost() = header;
rightmost() = header;
}