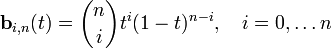贝塞尔曲线.简单推导与用opengl实现动态画出。

在opengl中，我们可以用少许的参数来描述一个曲线，其中贝塞尔曲线算是一种很常见的曲线控制方法，我们先来看维基百科里对贝塞尔曲线的说明：

线性贝塞尔曲线

给定点P₀、P₁，线性贝塞尔曲线只是一条两点之间的直线。这条线由下式给出：

且其等同于线性插值。

二次方贝塞尔曲线

二次方贝塞尔曲线的路径由给定点P₀、P₁、P₂的函数B（t）追踪：

。

TrueType字体就运用了以贝塞尔样条组成的二次贝塞尔曲线。

一些关于参数曲线的术语，有

即多项式

又称作n阶的伯恩斯坦基底多项式，定义0⁰ = 1。

点P_i称作贝塞尔曲线的控制点。多边形以带有线的贝塞尔点连接而成，起始于P₀并以P_n终止，称作贝塞尔多边形（或控制多边形）。贝塞尔多边形的凸包（convex hull）包含有贝塞尔曲线。

在这里贴这些，是因为让我们有个基本的理解，下面把维基百科里一个动态图放上，让大家有更清晰了解贝塞尔曲线是如何生成的。

然后我们来分析相应数据的产生。最简单的二点，其实就是线段的参数化，大家能简单得到f(t)=p0+(p1-p0)*t=(1-t)p0+t*p1.

二次方贝塞尔曲线话，我直接用下面的图给出相应过程。

对应的三次方贝塞尔曲线，我们会如下图来门简略说明。

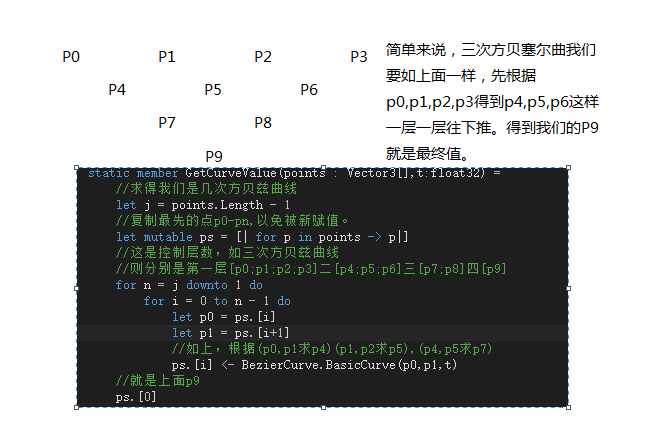
在上面，我们给出用我们推导的过程。下面是根据这个过程生成的主要代码。

type BezierCurve() =
    static member BasicCurve (p0:Vector3, p1:Vector3,t) = (1.f-t)*p0 + t*p1
    static member GetCurveValue(points : Vector3[],t:float32) =
        //求得我们是几次方贝兹曲线
        let j = points.Length - 1
        //复制最先的点p0-pn,以免被新赋值。
        let mutable ps = [| for p in points -> p|]
        //这是控制层数，如三次方贝兹曲线
        //则分别是第一层[p0;p1;p2;p3]二[p4;p5;p6]三[p7;p8]四[p9]
        for n = j downto 1 do 
            for i = 0 to n - 1 do
                let p0 = ps.[i]
                let p1 = ps.[i+1]
                //如上，根据(p0,p1求p4)(p1,p2求p5),(p4,p5求p7)
                ps.[i] <- BezierCurve.BasicCurve(p0,p1,t)
        //就是上面p9
        ps.[0]
    static member CreateCurve(points : Vector3[],count:int) =
        let ps = Array.create count Vector3.Zero
        let step = 1.f/float32 count
        let len = count - 1
        for i = 0 to len do
            ps.[i] <- BezierCurve.GetCurveValue(points,step * float32 i)
        ps
    static member GetCurveValueS(points : Vector3[],t:float32) =
        let j = points.Length - 1
        let mutable ps = [| for p in points -> p|]
        let mutable rs = [||]
        for n = j downto 1 do 
            for i = 0 to n - 1 do
                let p0 = ps.[i]
                let p1 = ps.[i+1]
                ps.[i] <- BezierCurve.BasicCurve(p0,p1,t)
            rs <- Array.append rs ps.[0 .. n-1]
        ps.[0],rs

BasicCurve就是我们线段的参数化，pt=p0+(p1-p0)*t=(1-t)p0+t*p1.

而GetCurveValue就是如上面所示，求多次方贝兹曲线在t(0<t<1)时的值。

而CreateCurve这个就是我们要生成的贝兹曲线在程序里的精度，值越高则画的点越多。看起来越逼真。

那下来，我们来生成如维基百科的那种动态图，也好加深的我们的印象。根据动态图，我们要知道的是，在t点，每一层相邻的二个点走到那了(也就是上面的GetCurveValueS的实现)，这里给出主要的代码。

    override v.OnRenderFrame(e) =
        base.OnRenderFrame e 
        GL.Clear (ClearBufferMask.ColorBufferBit ||| ClearBufferMask.DepthBufferBit)
        let mutable lookat = Matrix4.LookAt(caram.Eye,caram.Target,Vector3.UnitY)
        GL.MatrixMode(MatrixMode.Modelview)
        GL.LoadMatrix(&lookat)

        GL.Color3(Color.White)
        GL.VertexPointer(3,VertexPointerType.Float,0,vs)
        GL.DrawArrays(BeginMode.LineStrip,0,vs.Length)
        currentTime <- currentTime + e.Time
        if currentTime > totalTime  && frame < allFrame then
            frame <- frame + 1 
            let currentStep =float32 frame/float32 allFrame
            let v = BezierCurve.GetCurveValueS(vs,currentStep)
            ac <- Array.append ac [|fst v|]
            ps <- snd v
            currentTime <- currentTime - totalTime 
            printfn "ac:%A" ps  
        let mutable step = 0
        for i = vs.Length - 2 downto 1 do
            if ps.Length > step + i then
                let is = ps.[step .. step + i]
                GL.VertexPointer(3,VertexPointerType.Float,0,is)
                GL.DrawArrays(BeginMode.LineStrip,0,is.Length)
                step <- step + i + 1
                printfn "is:%A" is     
        GL.Color3(Color.Red)                      
        GL.VertexPointer(3,VertexPointerType.Float,0,ac)
        GL.DrawArrays(BeginMode.LineStrip,0,ac.Length)
        v.SwapBuffers()

在上面，我们用totalTime控制显示的快慢，用allFrame控制我们要显示的精度。frame表示当前t点的情况。

相关效果图：

下面给出相关源代码的附件

贝塞尔曲线

其中EDSF移动镜头，小键盘上的+与-分别控制动画的速度，R键重新开始画曲线过程。

贝塞尔曲面在opengl有比较容易的实现用求值器，下面是根据opengl红皮书的一个例子改的，定义一个数组，排列顺序按v,u,z来，u表示行，v表示每列，z表示是Vector3,Vector4的几个顶点，如：

       let vvs = [|
                //-1.5;-1.5;4.0; -0.5;-1.5;2.0; 0.5;-1.5;-1.0; 1.5;-1.5;2.0
                -1.5;-0.5;1.0; -0.5;-0.5;3.0; 0.5;-0.5;0.0;  1.5;-0.5;-1.0
                -1.5;0.5;4.0;  -0.5;0.5;0.0;  0.5;0.5;3.0;   1.5;0.5;4.0
                -1.5;1.5;-2.0; -0.5;1.5;-2.0; 0.5;1.5;0.0;   1.5;1.5;-1.0
                |]      
       //[3,4,3],组织如上面，三列四行，每行三点就是Vector3
        //数组格式[v][u][z] 则GL.Map2(MapTarget.Map2Vertexz,0.,1.,z,u,0.,1.,u*z,v,vvs)
        GL.Map2(MapTarget.Map2Vertex3,0.,1.,3,4,0.,1.,12,3,vvs)
        GL.MapGrid2(10,0.,1.,5,0.,1.)
        GL.EvalMesh2(MeshMode2.Line,0,10,0,5)    

这个贝塞尔曲面表示在u方向4个控制点，z方向有3个控制点，u的精细度是10，意思是u方向的线都是由10个点组成，v的精细度是5，精细度越高，线越光滑。效果图如下：

最后向法国工程师皮埃尔·贝塞尔致敬。