原文链接https://www.cnblogs.com/zhouzhendong/p/UOJ201.html
题解
首先把题目里面的提示抄过来:
结论:假设带权无向图 G 有 100 个节点 1000 条边,且所有权值各不相同。那么,G 中一定存在一个单调上升路径,它的长度大于等于 20。
证明:假设每个节点上有一个探险家。我们按权值从小到大枚举所有的边,每次将该边连接的节点中的探险家的位置进行对调。可以知道,每个探险家都走的是一条单调上升路径。另外,由于共有 100 个探险家,而探险家一共走了 2000 步,所以有人走了 20 步。证毕。
于是容易得知点数为 n 的完全图至少要走 n-1 步。
注意到 n 为偶数,那么我们来构造一下走n-1步的图。
我们考虑把所有的边分成 (n-1) 个大小为 n/2 的集合且同组的边没有端点重合。
于是我们只要把第一组标 1..n/2 ,第二组标 n/2+1...n, .... 即可。
关键是怎么构造。
看图:
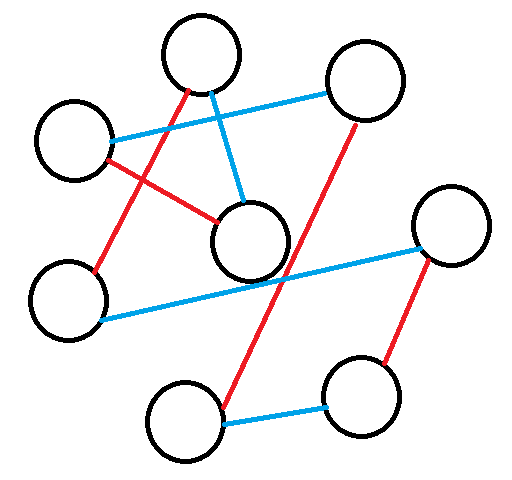
这里红的一组,蓝的一组,总共就类似这样的转 n-1 次就好了。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL read(){
LL x=0;
char ch=getchar();
while (!isdigit(ch))
ch=getchar();
while (isdigit(ch))
x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
const int N=505;
int n,k;
int cnt=0;
int g[N][N];
int nxt(int x){
return x==k?1:x+1;
}
int pre(int x){
return x==1?k:x-1;
}
int main(){
n=read();
k=n-((n&1)^1);
for (int i=1;i<=k;i++){
if (~n&1)
g[n][i]=g[i][n]=++cnt;
int x=i,y=i;
for (int j=1;j<=(n-1)/2;j++){
x=pre(x),y=nxt(y);
g[x][y]=g[y][x]=++cnt;
}
}
for (int i=1;i<=n;i++)
for (int j=i+1;j<=n;j++)
printf("%d ",g[i][j]);
return 0;
}