2021.01.07冬令营模拟

2020.01.07冬令营模拟

(22 ptes) 在欢声笑语中打出GG

 

T1. 球(qiu)

(Solution)

首先需要发现询问只在第一象限(确定了很重要!)，打个图出来我们可以发现第一象限中主要以一个个 (L) 型的等差数列构成：

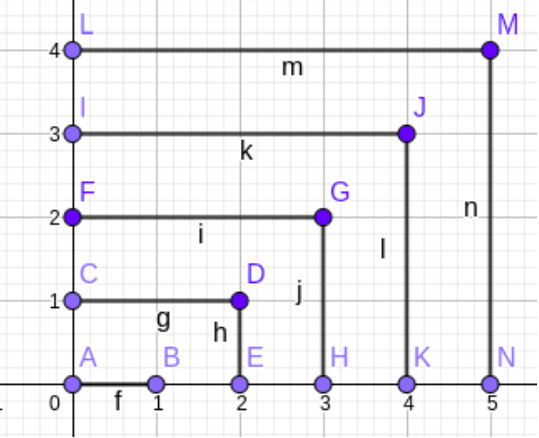
将询问容斥一下(成四个由 ((0, 0)) 开始的区间)，发现每个询问由嵌套的 (L) 和 一堆“横” (—) 或“竖” (|) 构成，选择一个容易计算的数(首或尾)减去，剩下的就是从零开始的等差数列很好计算，减去的数的和也很好计算，写出求和式套平方和公式和“立方和公式”即可。

平方和公式：(sum limits_{i = 1}^{n}{i ^ 2} = frac{n (n + 1) (2n + 1)}{6})。

“立方和公式”：(sum limits_{i = 1}^{n}{i^3} = (sum limits_{i = 1}^{n}{i})^2 = frac{n^2 (n + 1)^2}{4})

(Code)

#include <cstdio>

using namespace std;

#define ull unsigned long long

#define fo(i, x, y) for(int i = x; i <= y; i ++)

void read(ull &x) {
    char ch = getchar(); x = 0;
    while (ch < '0' || ch > '9') ch = getchar();
    while (ch >= '0' && ch <= '9') x = (x << 1) + (x << 3) + ch - 48, ch = getchar();
}

const ull mo = 1ull << 63;

ull Sqr(ull x) { return x * x; }

ull Sum1(ull x, ull y) {
    ull s1 = x + y, s2 = y - x + 1;
    (s1 & 1) ? (s2 >>= 1) : (s1 >>= 1);
    return s1 * s2;
}

ull Sum2(ull n) {
    ull s1 = n, s2 = n + 1, s3 = n << 1 | 1;
    (s1 & 1) ? ((s2 & 1) ? (s3 >>= 1) : (s2 >>= 1)) : (s1 >>= 1);
    (s1 % 3) ? ((s2 % 3) ? (s3 /= 3) : (s2 /= 3)) : (s1 /= 3);
    return s1 * s2 * s3;
}

ull min(ull x, ull y) { return x < y ? x : y; }

ull Calc(ull u, ull v) {
    ull sum = 0; ull k = min(u, v - 1), sk = Sum2(k);
    if (v > 1) {
        ull d = Sum1(1, k);
        sum = (Sqr(d) * 8 - sk * 8 + 3 * d) % mo;
    }
    if (u > k) {
        sum += v * ((Sum2(u) - sk) * 4 - Sum1(k + 1, u) * 5 + (u - k << 1));
        sum += Sum1(0, v - 1) * (u - k);
    } else if (v > k + 1) {
        -- v;
        sum += u * (((Sum2(v) - sk) * 4 - Sum1(k + 1, v) * 3 + (v - k)));
        sum -= Sum1(0, u - 1) * (v - k);
    }
    return sum;
}

int main() {
    freopen("qiu.in", "r", stdin);
    freopen("qiu.out", "w", stdout);

    ull Q, x1, x2, y1, y2;
    read(Q);
    fo(Case, 1, Q) {
       read(x1), read(x2), read(y1), read(y2);
        ++ x1, ++ x2, ++ y1, ++ y2;
        ull ans = Calc(y2, x2);
        if (x1 > 1) ans -= Calc(y2, x1 - 1);
        if (y1 > 1) ans -= Calc(y1 - 1, x2);
        if (x1 > 1 && y1 > 1)
            ans += Calc(y1 - 1, x1 - 1);
        printf("%llu
", ans % mo);
    }

    return 0;
}

 

T2. 星空(sky)

(Solution)

(22 ptes)

发现题目类似二分图最大匹配，建出图跑一遍最大费用最大流就可以了。

因为数组开小了没拿到 (a_i) 相同的 (7 ptes) 呢。

(100 ptes)

为了方便处理先排序(按 ((a_i, b_i)) 从小到大)，接着考虑模拟网络流的过程，分 (i < j) 和 (i > j) 讨论：

• 对于 (i < j)，相当于直接匹配，那么需要找到最大的 (b_j - b_i)，用线段树可以简单维护，支持删除单点即可。
• 对于 (i > j)，相当于我们需要找到一对之前的匹配 ((x, y)) 满足 (x < i < j < y)，将 ((x, y)) 退流并且匹配 ((x, i) (j, y))。考虑如何维护，我们可以在匹配一对 ((x, y) , x < y) 时将区间 ([x + 1, y - 1]) 加 (1)，匹配一对 ((i, j), i > j) 时将区间 ([i, j]) 减 (1)，那么 ((i, j)) 满足可以退流的条件即为区间 ([i, j]) 中的权值都 (geq 1)，同样可以用线段树维护。

再稍微糊一下区间加减时线段树如何维护：若加或减都不会对当前区间产生影响时(即无 (0 ightarrow 1) 或 (1 ightarrow 0))，直接打 (lazy) 标记走人，否则就继续 (dg) 下去。虽然不会证时间复杂度，但是感觉上是对的 (至少能过)。

(Code)

最后贴上丑丑的 (code)，线段树打得好丑！

#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

#define N 100000
#define inf 1000000000

#define fo(i, x, y) for(ll i = x; i <= y; i ++)
#define fd(i, x, y) for(ll i = x; i >= y; i --)

#define ll long long

void read(ll &x) {
    char ch = getchar(); x = 0;
    while (ch < '0' || ch > '9') ch = getchar();
    while (ch >= '0' && ch <= '9') x = (x << 1) + (x << 3) + ch - 48, ch = getchar();
}

struct Arr { ll x, y; } a[N + 1];

ll n;

namespace Tree {
    #define ls (t << 1)
    #define rs (t << 1 | 1)
    struct My { ll ln, rx, sx, lt, rt; } t1[N << 2], t2[N << 2];
    Arr g1[N << 2], g2[N << 2];
    ll lz[N << 2], ms[N << 2], mx[N << 2];
    void Pushd(int t, int l, int r) {
        if (! lz[t]) return;
        ms[t] += lz[t], mx[t] += lz[t];
        if (! mx[t]) {
            t2[t] = (My) { inf, -inf, -1, 0, 0 };
            g2[t] = (Arr) { 0, 0 };
        } else if (ms[t]) {
            t2[t].ln = t1[t].ln, t2[t].rx = t1[t].rx, g2[t] = g1[t];
            if (l < r && t1[ls].rx - t1[rs].ln > t2[t].sx)
                t2[t].sx = t1[ls].rx - t1[rs].ln, t2[t].lt = g1[ls].y, t2[t].rt = g1[rs].x;
            else
                if (l == r)
                    t1[t].sx = 0, t2[t].lt = l, t2[t].rt = l;
        }
        if (l < r)
            lz[ls] += lz[t], lz[rs] += lz[t];
        lz[t] = 0;
    }
    void Pushu(int t, int l, int r, int mid) {
        Pushd(ls, l, mid), Pushd(rs, mid + 1, r);
        ms[t] = min(ms[ls], ms[rs]), mx[t] = max(mx[ls], mx[rs]);
        t1[t] = t1[ls].sx > t1[rs].sx ? t1[ls] : t1[rs];
        t1[t].ln = t1[ls].ln < t1[rs].ln ? (g1[t].x = g1[ls].x, t1[ls].ln) : (g1[t].x = g1[rs].x, t1[rs].ln);
        t1[t].rx = t1[ls].rx > t1[rs].rx ? (g1[t].y = g1[ls].y, t1[ls].rx) : (g1[t].y = g1[rs].y, t1[rs].rx);
        if (t1[rs].rx - t1[ls].ln > t1[t].sx)
            t1[t].sx = t1[rs].rx - t1[ls].ln, t1[t].lt = g1[ls].x, t1[t].rt = g1[rs].y;
        t2[t] = t2[ls].sx > t2[rs].sx ? t2[ls] : t2[rs];
        t2[t].ln = t2[ls].ln, g2[t].x = g2[ls].x;
        t2[t].rx = t2[rs].rx, g2[t].y = g2[rs].y;
        if (t2[ls].rx - t2[rs].ln > t2[t].sx)
            t2[t].sx = t2[ls].rx - t2[rs].ln, t2[t].lt = g2[ls].y, t2[t].rt = g2[rs].x;
        if (ms[ls] > 0 && t2[rs].ln < t2[t].ln)
            t2[t].ln = t2[rs].ln, g2[t].x = g2[rs].x;
        if (ms[rs] > 0 && t2[ls].rx > t2[t].rx)
            t2[t].rx = t2[ls].rx, g2[t].y = g2[ls].y;
            
    }
    void Build(int t, int l, int r) {
        if (l == r) {
            t1[t] = (My) { a[l].y, a[l].y, 0, l, l };
            g1[t] = (Arr) { l, l };
            t2[t] = (My) { inf, -inf, -1, 0, 0 };
            g2[t] = (Arr) { 0, 0 };
            ms[t] = mx[t] = lz[t] = 0;
            return;
        }
        int mid = l + r >> 1;
        Build(ls, l, mid), Build(rs, mid + 1, r);
        Pushu(t, l, r, mid);
    }
    void De(int t, int l, int r, int k) {
        Pushd(t, l, r);
        if (l == r) {
            t1[t] = t2[t] = (My) { inf, -inf, -1, 0, 0 };
            g1[t] = g2[t] = (Arr) { 0, 0 };
            return;
        }
        int mid = l + r >> 1;
        k <= mid ? De(ls, l, mid, k) : De(rs, mid + 1, r, k);
        Pushu(t, l, r, mid);
    }
    void Add(int t, int l, int r, int x, int y, int d) {
        Pushd(t, l, r);
        int mid = l + r >> 1;
        if (x <= l && r <= y) {
            if (ms[t] > 1 || (mx[t] == 1 && d == -1) || l == r) {
                lz[t] = d; Pushd(t, l, r);
                return;
            }
            Add(ls, l, mid, x, y, d), Add(rs, mid + 1, r, x, y, d);
            Pushu(t, l, r, mid);
            return;
        }
        if (x <= mid) Add(ls, l, mid, x, y, d);
        if (y > mid) Add(rs, mid + 1, r, x, y, d);
        Pushu(t, l, r, mid);
    }
    #undef ls
    #undef rs
}

bool Cmp(Arr a, Arr b) { return a.x < b.x || (a.x == b.x && a.y < b.y); }

using namespace Tree;

int main() {
    freopen("sky.in", "r", stdin);
    freopen("sky.out", "w", stdout);

    read(n);
    fo(i, 1, n) read(a[i].x), read(a[i].y);

    sort(a + 1, a + 1 + n, Cmp);
    Build(1, 1, n);
    ll ans = 0;
    fo(i, 1, (n >> 1)) {
        if (t1[1].sx <= 0 && t2[1].sx <= 0) {
            printf("%lld
", ans); continue;
        }
        if (t1[1].sx > t2[1].sx) {
            ans += t1[1].sx;
            ll lt1 = t1[1].lt, rt1 = t1[1].rt;
           if (lt1 < rt1 - 1)
               Add(1, 1, n, lt1 + 1, rt1 - 1, 1);
            De(1, 1, n, lt1), De(1, 1, n, rt1);
        } else {
            ans += t2[1].sx;
            ll lt1 = t2[1].lt, rt1 = t2[1].rt;
            Add(1, 1, n, lt1, rt1, -1);
            De(1, 1, n, lt1), De(1, 1, n, rt1);
        }
        printf("%lld
", ans);
    }

    return 0;
}