Loj2083.「NOI2016」优秀的拆分

「NOI2016」优秀的拆分

#2083. 「NOI2016」优秀的拆分 - 题目 - LibreOJ (loj.ac)

 

(Description)

求将字符串 (S) 所有子串拆分为 (AABB) 形式的总个数。

 

(Solution)

令 (f_{i}) 表示以位置 (i) 开头的 (AA) 串的个数，(g_i) 表示以位置 (i) 结尾的 (AA) 串的个数。

那么最后答案为 (sum g_i f_{i + 1})

字符串 (hash) 可以 (O(n^2)) 暴力求出 (f_i)，瓶颈在于如何快速求出 (f_i)。

考虑求所有长度为 (2len) 的 (AA) 串，将原串每 (len) 位设置关键点，可以发现每个 (AA) 串一定经过两个关键点。

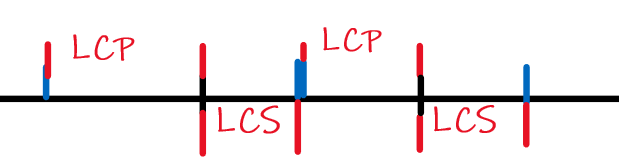
发现可以以关键点为界将 (A) 分为 (LCP) 和 (LCS)。

考虑求出两个相邻关键点 (x, y) 的 (lcp) 和 (lcs)，可以发现能形成 (AA) 串的充要条件是 (lcp + lcs > len)，并且形成 (AA) 串的开头为一段区间 ([x - lcp + 1, x + lcs - len])，结尾类似。

求出原串正反的 (sa)，总时间复杂度 (O(n log n))。

 

(Code)

nclude <bits/stdc++.h>

using namespace std;

#define N 30000
#define L 15

#define fo(i, x, y) for(int i = x; i <= y; i ++)
#define fd(i, x, y) for(int i = x; i >= y; i --)
#define mcp(a, b) memcpy(a, b, sizeof b)
#define Mes(a, x) memset(a, x, sizeof a)

int sl[N + 1], sr[N + 1], Log[N + 1];
int n;

struct SA {
    int sa[N + 1], rk[N + 1], ht[N + 1], id[N + 1], oldrk[N << 1], buc[N + 1], px[N + 1], ft[N + 1][L + 1];
    int sk;
    void mysort() {
        fill(buc, buc + 1 + sk, 0);
        fo(i, 1, n) ++ buc[ px[i] = rk[id[i]] ];
        fo(i, 1, sk) buc[i] += buc[i - 1];
        fd(i, n, 1) sa[ buc[px[i]] -- ] = id[i];
    }
    bool pd(int x, int y, int z) { return oldrk[x] == oldrk[y] && oldrk[x + z] == oldrk[y + z]; }
    void build(char ch[]) {
        Mes(rk, 0), Mes(oldrk, 0);
        sk = 26;
        fo(i, 1, n) rk[ id[i] = i ] = ch[i] - 'a' + 1;
        mysort();
        for (int w = 1, p = 0; w <= n; w <<= 1, p = 0) {
            fo(i, n - w + 1, n) id[ ++ p ] = i;
            fo(i, 1, n) if (sa[i] > w)
                id[ ++ p ] = sa[i] - w;
            mysort();
            mcp(oldrk, rk);
            sk = 0;
            fo(i, 1, n)
                rk[sa[i]] = pd(sa[i], sa[i - 1], w) ? sk : ++ sk;
            if (sk == n) {
                fo(i, 1, n) sa[rk[i]] = i;
                break;
            }
        }
        sk = 0;
        fo(i, 1, n) {
            if (sk) -- sk;
            while (ch[i + sk] == ch[sa[rk[i] - 1] + sk])
                ++ sk;
            ht[rk[i]] = sk;
        }
        fo(i, 1, n) ft[i][0] = ht[i];
        fo(j, 0, L - 1) fo(i, 1, n)
            ft[i][j + 1] = (i + (1 << j) <= n) ? min(ft[i][j], ft[i + (1 << j)][j]) : ft[i][j];
    }
    int dt;
    int get(int l, int r) {
        l = rk[l], r = rk[r];
        if (l > r) swap(l, r);
        if (++ l == r) return ft[l][0];
        dt = Log[r - l + 1];
        return min(ft[l][dt], ft[r - (1 << dt) + 1][dt]);
    }
} s1, s2;

char ch[N + 1];
int main() {
    int T; scanf("%d
", &T);
    Log[1] = 0;
    fo(i, 2, N)
        Log[i] = Log[i >> 1] + 1;
    while (T --) {
        scanf("%s
", ch + 1);
        n = strlen(ch + 1);
        s1.build(ch);
        fd(i, (n >> 1), 1)
            swap(ch[i], ch[n - i + 1]);
        s2.build(ch);
        fill(sl + 1, sl + 1 + n, 0);
        fill(sr + 1, sr + 1 + n, 0);
        int l, r, lcp, lcs, dlen, pl, pr;
        fd(len, (n >> 1), 1) {
            fd(k, (n / len) - 1, 1) {
                l = len * k, r = len * (k + 1);
                lcs = s1.get(l, r);
                lcp = s2.get(n - l + 1, n - r + 1);
                if (lcp + lcs > len) {
                    lcp = min(lcp, len), lcs = min(lcs, len);
                    dlen = lcp + lcs - len - 1;
                    ++ sl[l - lcp + 1], -- sl[l - lcp + 1 + dlen + 1];
                    ++ sr[r + lcs - 1], -- sr[r + lcs - 1 - dlen - 1];
                }
            }
        }
        fo(i, 2, n) sl[i] += sl[i - 1];
        fd(i, n - 1, 1) sr[i] += sr[i + 1];
        long long ans = 0;
        fo(i, 2, n) ans += 1ll * sr[i - 1] * sl[i];
        printf("%lld
", ans);
    }
    return 0;
}