Logistic回归也是一种分类算法,其主要思想是:根据现有数据对分类边界建立回归公式,以此进行分类。
简单的说就是采用Logistic回归函数,接受所有的特征值输入,然后输出类别。
Logistic函数又叫sigmoid函数:
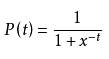
形状为:

从上图容易看出,输入t,在x!=0的情况下,P(t)大于0.5 或小于0.5。通常,P(t)>0.5则认为t属于类别1,P(t)<0.5,则认为t属于类别0。(可见Logistic回归算法擅长处理二分类问题)
那么问题转化为:如何把给定的特征值集合映射为一个合适的输入t?
我们可以给每个特征的所有属性都乘以一个回归系数,然后把所有的结果值相加,讲这个总和带入sigmoid函数中,进而得到一个范围在0~1之间的数值。
特征:X = (x0,x1,x2,...,xn)
回归系数:W = (w0,w1,w2,...,wn)
输入t=XW = w0*x0 + w1*x1 + w2*x2 + ... + wn*xn
现在,问题又变成了:如何确定最佳回归系数?
先来看看这个函数:
可以说这个函数代表了sigmoid函数预测的准确程度,如果有N个训练值,则似然函数就是这N个概率的乘积:
现在,问题又转化为求最大值的问题?
我们知道求函数的最大值或最小值可以通过斜率,向着斜率不断增大的方向不断前进,可以得到函数的局部最大值,对于sigmoid函数来说,向着无穷大方向,局部最大值既是整体的最大值。
采用梯度上升算法用来求函数的最大值,梯度上升法的基本思想是:要找到某函数的最大值,最好的方法是沿着该函数的梯度方向探寻。
梯度上升算法的迭代公式: ,该公式将一直被迭代执行,直到达到某个停止条件,比如迭代次数达到某个指定的值或算法达到某个可以允许的误差范围。
,该公式将一直被迭代执行,直到达到某个停止条件,比如迭代次数达到某个指定的值或算法达到某个可以允许的误差范围。
《机器学习实战》书中给出的梯度上升迭代code:
alpha = 0.001 maxCycles = 500 weights = ones((n,1)) for k in range(maxCycles): #heavy on matrix operations h = sigmoid(dataMatrix*weights) #matrix mult error = (labelMat - h) #vector subtraction weights = weights + alpha * dataMatrix.transpose()* error #matrix mult
alpha是每次迭代增加的步长,maxCycles是循环次数,weights是最终要求的W,dataMatrix是训练数据矩阵,初始Weights置为全1的矩阵,h为训练数据的sigmoid分类,labelMat为训练数据的真实分类,error即为迭代过程中的分类的误差,重点是在weights = weights + alpha * dataMatrix.transpose()* error,训练矩阵的转置矩阵乘以误差矩阵,得到一个数字,这个数字再乘以步长加上原weights得到一个新的weights。这段代码相当于沿着斜率的最大值方向前进了步长alpha,为什么呢,书的作者没有给出解释,我的理解是训练数据可定是想着往训练结果labelMat上尽量靠拢,这样训练出来的weights才有价值,训练数据转置矩阵乘以error矩阵以为着向正确的方向修正了error,然后原方向(weights)往着修正的方向前进一个步长(alpha)。迭代500次之后得到的weights做为最终的W。
当然也可以采用随机梯度上升算法来提升算法的效率,从上面的代码可以看到,每次迭代都会把所有的训练数据相成一次,随机梯度上升算法是每次选取训练数据的一行,进行迭代,可以大大降低迭代的计算量。
def stocGradAscent0(dataMatrix, classLabels): m,n = shape(dataMatrix) alpha = 0.01 weights = ones(n) for i in range(m): h = sigmoid(sum(dataMatrix[i]*weights)) error = classLabels[i] - h weights = weights + alpha * dataMatrix[i]* error