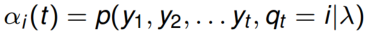在中文标注时,除了条件随机场(crf),被提到次数挺多的还有隐马尔可夫(HMM),通过对《统计学习方法》一书的学习,我对HMM的理解进一步加深了。
第一部分 介绍隐马尔可夫
隐马尔可夫模型是马尔可夫链的一种,它的状态不能直接观察到,但能通过观测向量序列观察到,每个观测向量都是通过某些概率密度分布表现为各种状态,每一个观测向量是由一个具有相应概率密度分布的状态序列产生。
这样一说可能会有点复杂,给个例子可能会好一点。就拿我们读初高中时的概率问题来作为例子吧。
已知有一个密度均匀的六面色子,能掷出1、2、3、4、5、6,。那么现在掷四次色子,掷出结果为{2,3,2,7}的概率为 。这一点毫无疑问。
。这一点毫无疑问。
但是如果再加一个密度均匀的四面色子,能掷出1,2,3,4。现在随机掷四次色子,每次掷的色子可能为六面色也可能为四面色,掷出{2,3,2,7}的概率又应该为多少呢?这就要看每次掷的色子是六面色还是四面色的概率以及当前色掷出当前结果的概率为多少了。此时观测序列是{2,3,2,7},这是已知的,而状态序列则是每次掷的是哪个色子所组成的序列,这是未知的。
状态转移概率图如下:
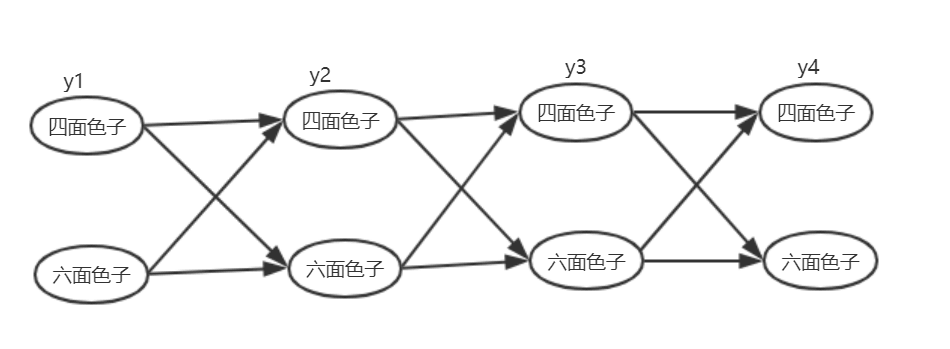
生成观测序列概率图如下:
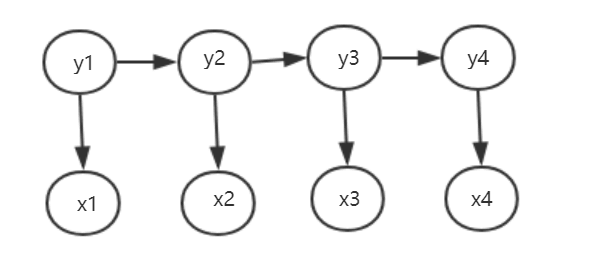
这既是隐马尔可夫模型
第二部分 前向算法
由于状态序列未知,而且可能有很多种,所以根据观测序列求概率求起来十分麻烦,由此引出前向算法。
前向概率的定义是:当第t个时刻的状态为i时,前面的时刻分别观测到y1,y2, ..., yt的概率,即:
计算步骤是:
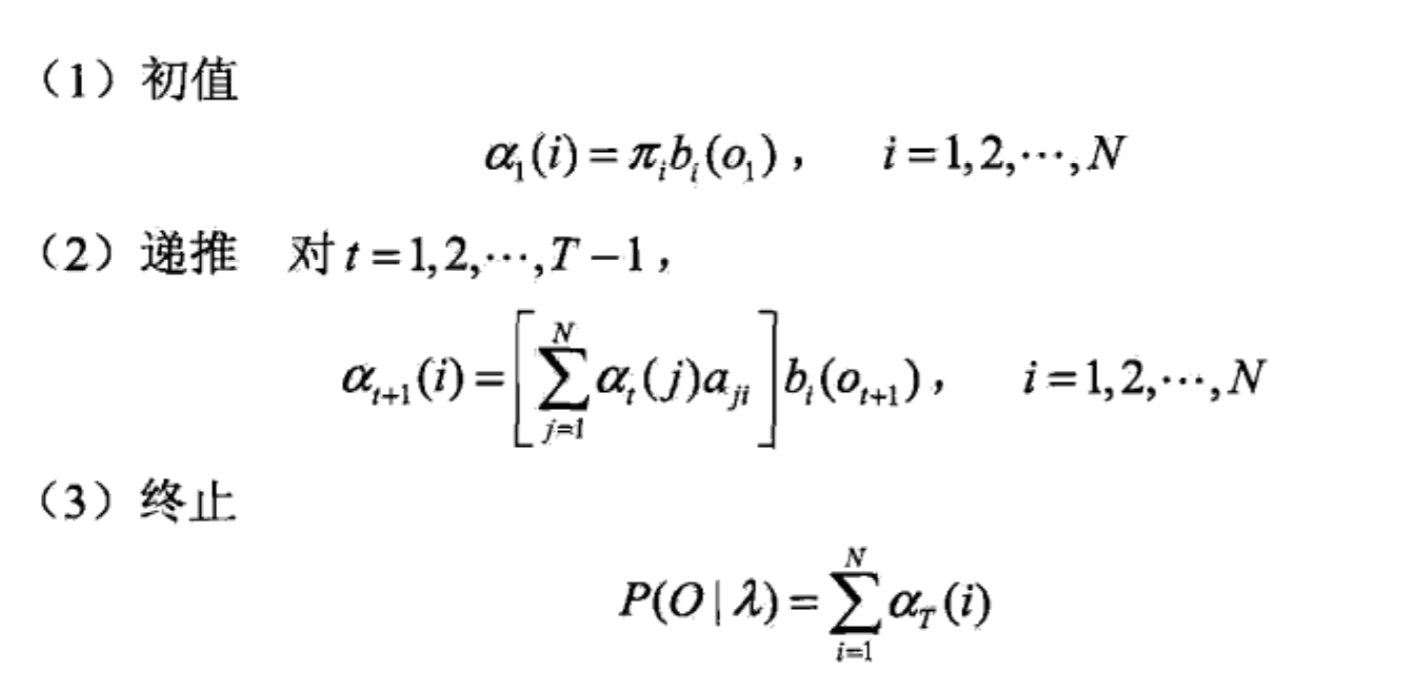
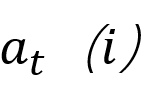 为t时刻状态为i的概率,
为t时刻状态为i的概率,![]() 为i状态转化为j状态的概,
为i状态转化为j状态的概,![]() 为i状态产生对应时刻的观测值的概率
为i状态产生对应时刻的观测值的概率