1 clc; 2 clear all; 3 close all; 4 M=9;% 维度,几个参数 5 nPop=200; 6 VarMin=[0.6, 0.10, 0.002, 0.02, 0.17, 0.0, 0.17, 0.0, 0.0];%各个参数下限 7 VarMax=[2.0, 0.49, 0.05, 0.30, 2.6, 0.0, 1.30, 0.99, 5.0];%各个参数上限 8 p = sobolset(M); 9 % R=p(1:nPop,:);% 我只用前nPop个 10 R=[]; 11 for i=1:nPop 12 r=p(i,:); 13 r=VarMin+r.*(VarMax-VarMin); 14 R=[R; r]; 15 end 16 plot(R(:,1),'b*')
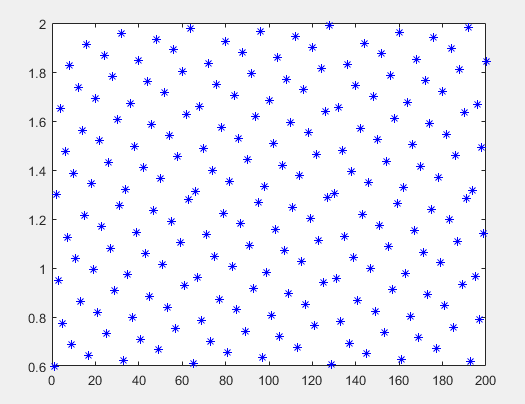
当然,matlab中还有其余的抽样类型:
Construct Halton quasi-random point set、Latin hypercube sample、Construct Sobol quasi-random point set、Continuous uniform random numbers
Syntax
p = haltonset(d)
p = haltonset(d,prop1,val1,prop2,val2,...)
Description
p = haltonset(d) constructs a d-dimensional point set p of the haltonset class, with default property settings.
p = haltonset(d, specifies property name/value pairs used to construct prop1,val1,prop2,val2,...)p.
The object p returned by haltonset encapsulates properties of a specified quasi-random sequence. The point set is finite, with a length determined by the Skip and Leap properties and by limits on the size of point set indices (maximum value of 253). Values of the point set are not generated and stored in memory until you access p using net or parenthesis indexing.
Examples
Generate a 3-D Halton point set, skip the first 1000 values, and then retain every 101st point:
p = haltonset(3,'Skip',1e3,'Leap',1e2)
p =
Halton point set in 3 dimensions (8.918019e+013 points)
Properties:
Skip : 1000
Leap : 100
ScrambleMethod : none
Use scramble to apply reverse-radix scrambling:
p = scramble(p,'RR2')
p =
Halton point set in 3 dimensions (8.918019e+013 points)
Properties:
Skip : 1000
Leap : 100
ScrambleMethod : RR2
Use net to generate the first four points:
X0 = net(p,4)
X0 =
0.0928 0.6950 0.0029
0.6958 0.2958 0.8269
0.3013 0.6497 0.4141
0.9087 0.7883 0.2166
Use parenthesis indexing to generate every third point, up to the 11th point:
X = p(1:3:11,:)
X =
0.0928 0.6950 0.0029
0.9087 0.7883 0.2166
0.3843 0.9840 0.9878
0.6831 0.7357 0.7923
References
[1] Kocis, L., and W. J. Whiten. "Computational Investigations of Low-Discrepancy Sequences." ACM Transactions on Mathematical Software. Vol. 23, No. 2, 1997, pp. 266–294.
lhsdesign
Latin hypercube sample
Syntax
X = lhsdesign(n,p)
X = lhsdesign(...,'smooth','off')
X = lhsdesign(...,'criterion',criterion)
X = lhsdesign(...,'iterations',k)
Description
X = lhsdesign(n,p) returns an n-by-p matrix, X, containing a latin hypercube sample of n values on each of p variables. For each column of X, then values are randomly distributed with one from each interval (0,1/n), (1/n,2/n), ..., (1-1/n,1), and they are randomly permuted.
X = lhsdesign(...,'smooth','off') produces points at the midpoints of the above intervals: 0.5/n, 1.5/n, ..., 1-0.5/n. The default is 'on'.
X = lhsdesign(...,'criterion', iteratively generates latin hypercube samples to find the best one according to criterion)criterion, which can be 'none', 'maximin', or 'correlation'.
| Criterion | Description |
|---|---|
|
|
No iteration. |
|
|
Maximize minimum distance between points. This is the default. |
|
|
Reduce correlation. |
X = lhsdesign(...,'iterations',k) iterates up to k times in an attempt to improve the design according to the specified criterion. The default isk = 5.
Syntax
p = sobolset(d)
p = sobolset(d,prop1,val1,prop2,val2,...)
Description
p = sobolset(d) constructs a d-dimensional point set p of the sobolset class, with default property settings.
p = sobolset(d, specifies property name/value pairs used to construct prop1,val1,prop2,val2,...)p.
The object p returned by sobolset encapsulates properties of a specified quasi-random sequence. The point set is finite, with a length determined by the Skip and Leap properties and by limits on the size of point set indices (maximum value of 253). Values of the point set are not generated and stored in memory until you access p using net or parenthesis indexing.
Examples
Generate a 3-D Sobol point set, skip the first 1000 values, and then retain every 101st point:
p = sobolset(3,'Skip',1e3,'Leap',1e2)
p =
Sobol point set in 3 dimensions (8.918019e+013 points)
Properties:
Skip : 1000
Leap : 100
ScrambleMethod : none
PointOrder : standard
Use scramble to apply a random linear scramble combined with a random digital shift:
p = scramble(p,'MatousekAffineOwen')
p =
Sobol point set in 3 dimensions (8.918019e+013 points)
Properties:
Skip : 1000
Leap : 100
ScrambleMethod : MatousekAffineOwen
PointOrder : standard
Use net to generate the first four points:
X0 = net(p,4)
X0 =
0.7601 0.5919 0.9529
0.1795 0.0856 0.0491
0.5488 0.0785 0.8483
0.3882 0.8771 0.8755
Use parenthesis indexing to generate every third point, up to the 11th point:
X = p(1:3:11,:)
X =
0.7601 0.5919 0.9529
0.3882 0.8771 0.8755
0.6905 0.4951 0.8464
0.1955 0.5679 0.3192
References
[1] Bratley, P., and B. L. Fox. "Algorithm 659 Implementing Sobol's Quasirandom Sequence Generator." ACM Transactions on Mathematical Software. Vol. 14, No. 1, 1988, pp. 88–100.
[2] Joe, S., and F. Y. Kuo. "Remark on Algorithm 659: Implementing Sobol's Quasirandom Sequence Generator." ACM Transactions on Mathematical Software. Vol. 29, No. 1, 2003, pp. 49–57.
[3] Hong, H. S., and F. J. Hickernell. "Algorithm 823: Implementing Scrambled Digital Sequences." ACM Transactions on Mathematical Software. Vol. 29, No. 2, 2003, pp. 95–109.
[4] Matousek, J. "On the L2-Discrepancy for Anchored Boxes." Journal of Complexity. Vol. 14, No. 4, 1998, pp. 527–556.
Syntax
R = unifrnd(A,B)
R = unifrnd(A,B,m,n,...)
R = unifrnd(A,B,[m,n,...])
Description
R = unifrnd(A,B) returns an array R of random numbers generated from the continuous uniform distributions with lower and upper endpoints specified by A and B, respectively. If A and B are arrays, R(i,j) is generated from the distribution specified by the corresponding elements of A andB. If either A or B is a scalar, it is expanded to the size of the other input.
R = unifrnd(A,B,m,n,...) or R = unifrnd(A,B,[m,n,...]) returns an m-by-n-by-... array. If A and B are scalars, all elements of R are generated from the same distribution. If either A or B is an array, they must be m-by-n-by-... .
Examples
Generate one random number each from the continuous uniform distributions on the intervals (0,1), (0,2), ..., (0,5):
a = 0; b = 1:5;
r1 = unifrnd(a,b)
r1 =
0.8147 1.8116 0.3810 3.6535 3.1618
Generate five random numbers each from the same distributions:
B = repmat(b,5,1);
R = unifrnd(a,B)
R =
0.0975 0.3152 0.4257 2.6230 3.7887
0.2785 1.9412 1.2653 0.1428 3.7157
0.5469 1.9143 2.7472 3.3965 1.9611
0.9575 0.9708 2.3766 3.7360 3.2774
0.9649 1.6006 2.8785 2.7149 0.8559
Generate five random numbers from the continuous uniform distribution on (0,2):
r2 = unifrnd(a,b(2),1,5)
r2 =
1.4121 0.0637 0.5538 0.0923 0.1943
More About
Introduced before R2006a