【问题】在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。即输出P%1000000007
输入描述:
题目保证输入的数组中没有的相同的数字
数据范围:
对于%50的数据,size<=10^4
对于%75的数据,size<=10^5
对于%100的数据,size<=2*10^5
【思路】基于归并排序的思想统计逆序对:先把数组分割成子数组,再子数组合并的过程中统计逆序对的数目。统计逆序对时,先统计子数组内部的逆序对的数目,再统计相邻子数组的逆序对数目。
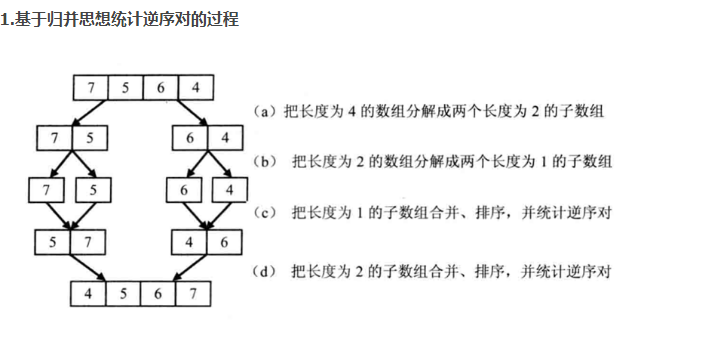
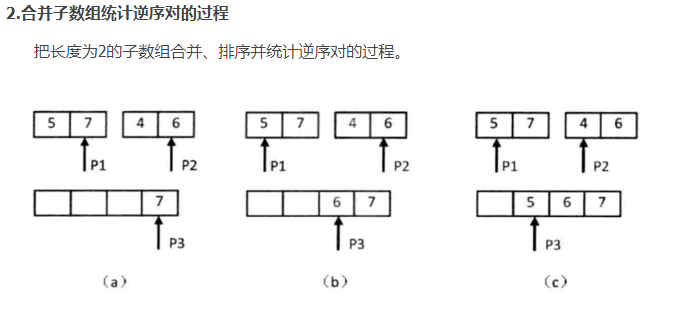
注:图中省略了最后一步,即复制第二个子数组最后剩余的4到辅助数组中。(a) P1指向的数字大于P2指向的数字,表明数组中存在逆序对。P2指向的数字是第二个子数组的第二个数字,因此第二个子数组中有两个数字比7小。把逆序对数目加2,并把7复制到辅助数组,向前移动P1和P3。(b) P1指向的数字小于P2指向的数字,没有逆序对。把P2指向的数字复制到辅助数组,并向前移动P2和P3. (c) P1指向的数字大于P2指向的数字,因此存在逆序对。由于P2指向的数字是第二个子数组的第一个数字,子数组中只有一个数字比5小。把逆序对数目加1,并把5复制到辅助数组,向前移动P1和P3。
#include <iostream> #include <vector> using namespace std; class Solution{ public: int count=0; int InversePairs(vector<int> data) { // 检查边界条件 if(data.size() != 0) { MergeSort(data,0,data.size()-1); } return count; } private: void MergeSort(vector<int> a, int l, int r) { /* 将长度为n的输入序列分成两个长度为n/2的子序列 */ if (l < r) { /* 中间元素*/ int m = (l + r) >>1; // 递归拆分 MergeSort(a, l, m); MergeSort(a, m + 1, r); // 递归合并 Merge(a, l, m, r); } } void Merge(vector<int> a, int l, int m, int r) { vector<int> t; //int p = 0; /* p指向辅助数组 */ int i = l; /* i指向第一个子表 */ int j = m + 1;/* j指向第二个子表 */ /* 两个子表都不为空时 */ while(i <= m && j <= r) { /* 取关键字小的元素转移至临时数组 */ if (a[i] > a[j]) { t.push_back(a[j++]); count=(count+m-i+1)%1000000007; } else t.push_back(a[i++]); } while(i <= m) t.push_back(a[i++]);/* 将非空的输入区间转移至输出区间 */ while(j <= r) t.push_back(a[j++]); for (i = 0; i < t.size(); i++) a[l + i] = t[i];/* 归并完成后将结果复制到原输入数组 */ } }; int main() { vector<int> a = {8,7,6,5,455,88,888,9999,546,46548,1315,445,554,111,5222,2264,8,331,454548}; Solution solution; solution.InversePairs(a); return 0; }