【总结】01背包问题

（蒟蒻的总结并不能代表什么，只能说给以后的自己，防止后来忘记吧？？可能有不对的地方，请指出）

没有算法标签

在学习OI好几个月后回来再看这个总结，发现原本写的二维的是错的，特此更正2019.6.18（开心的金明二维的痛）

---

让我们先附上一个01背包问题的基本题目：

给定 n 种物品和一个容量为 C 的背包，物品 i 的重量是 wi，其价值为 vi 。

问：应该如何选择装入背包的物品，使得装入背包中的物品的总价值最大？

首先先是头文件们以及定义们(还有输入）：

#inlcude<iostream>
#include<cstdio>
#include<algorithm>
#include<string>
#include<cstring>
#incude<camth>//把我所记住的头文件全写上了（大家不要学我）； 
using namespace std;
int n,c;//定义物品数量及背包容量； 
int w[1000],v[1000];//定义数组w[i]和v[i]分别表示物品i的质量和价值(1000毫无意义）； 
int f[1000][1000];//定义数组f[i][j]存放第i个时的当前最大值（乱说胡话）； 
int main()
{
    cin>>n>>c;//输入n，c； 
    for(int i=1;i<=n;i++)
    cin>>w[i]>>v[i];//输入第1~n个物体的质量和价值 ； 
    

接下来是时候发挥数组f的作用了。数组f存的是搜索（不是搜索）第i个物品时的最大价值。利用双层循环，设数组f[i][j]为第i个物品时恰好质量为j（这里有一点贪心？？？）的最大值，显然到f[i][j]时有两种可能：

1. 不选取第i个物品，则此时最大值为f[i-1][j]；
2. 选取第i个物品，则此时的最大值是f[i-1][j-w[i]]+v[i];（这里有必要解释一下：因为选取第i个物品后恰好装满j的容积，那么在没选取第i个物品时，恰好装满的是j-w[i]的容积。那么选取第i个物品之前的最大值就为f[i-1][j-w[i]]，这时再加上第i个物品的价值，得到结果。

显然我们要取这两种中最大的一种：利用函数max，则有：

for(int i=1;i<=n;i++)
        for(int j=c;j>=0;j--)
        if(j-w[i]>=0)f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i]);
        else f[i][j]=f[i-1][j];

当循环结束时，我们就求得了最大总价值f[n][c];

这里附上表帮助理解：

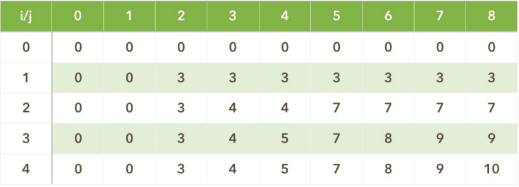
 附上完整代码：

#inlcude<iostream>
#include<cstdio>
#include<algorithm>
#include<string>
#include<cstring>
#incude<camth>//把我所记住的头文件全写上了（大家不要学我）； 
using namespace std;
int n,c;//定义物品数量及背包容量； 
int w[1000],v[1000];//定义数组w[i]和v[i]分别表示物品i的质量和价值(1000毫无意义）； 
int f[1000][1000];//定义数组f[i][j]存放第i个时的当前最大值（乱说胡话）； 
int main()
{
    cin>>n>>c;//输入n，c； 
    for(int i=1;i<=n;i++)
    cin>>w[i]>>v[i];//输入第1~n个物体的质量和价值 ； 
    for(int i=1;i<=n;i++)
        for(int j=c;j>=0;j--){//从c开始倒叙搜索并j>=w[i]是为了防止出现负下标
        if(j-w[i]>=0)f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i]);
        else f[i][j]=f[i-1][j];
    cout<<f[n][c]<<endl;

显然数组会很占空间，所以我们优化为一维数组（尽管没太听懂）：

#inlcude<iostream>
#include<cstdio>
#include<algorithm>
#include<string>
#include<cstring>
#incude<camth>//把我所记住的头文件全写上了（大家不要学我）； 
using namespace std;
int n,c;//定义物品数量及背包容量； 
int w[1000],v[1000];//定义数组w[i]和v[i]分别表示物品i的质量和价值(1000毫无意义）； 
int f[1000];//定义数组f[i][j]存放第i个时的当前最大值（乱说胡话）； 
int main()
{
    cin>>n>>c;//输入n，c； 
    for(int i=1;i<=n;i++)
    cin>>w[i]>>v[i];//输入第1~n个物体的质量和价值 ； 
    for(int i=1;i<=n;i++)
        for(int j=c;j>=w[i];j--)
        f[j]=max(f[j],f[j-w[i]]+v[i]);
    cout<<f[c]<<endl;//希望没输错……

end-