- 4.4上午：数学基础
（qwq整成word和cpp了，它居然不能直接把文档附上来）
- part 1：高精度运算
高精加和高精减就不说了，之前写过博客了qwq，讲一讲高精乘和高精除吧。
1.高精度乘法（不知道为甚么害怕自己忘了老想再写一遍）：
题干（就很简单惹）：给定两个数a，b，求他们的乘积（a和b都很大）；
显然如果直接乘，用一个数组存的话，可能会爆掉，（_int128也会爆的qwq），这时或许可以考虑将每一位分开存，然后就引入了神奇的高精度：
先读入两个数：这里用的是字符串char读入然后把每一位数字存到数组中：
for(int i = lena-1;i >= 0;i--)a[lena-i] = a1[i]-48;//把字符串存进数组中 for(int i = lenb-1;i >= 0;i--)b[lenb-i] = b1[i]-48; /*刚刚搞了个大乌龙qwq（直接 a[lena-i] = a1[lena]-48;b[lenb-i] = b1[lenb]-48;*/ /*插入的主要代码qwq，lena，lenb分别为字符串a1，b1的长度。这里从1~len分别存从个位到x位的数字*/
首先有一个必须要解决的问题：乘出来的数应该存到哪一位？？不妨模拟一下乘法计算：
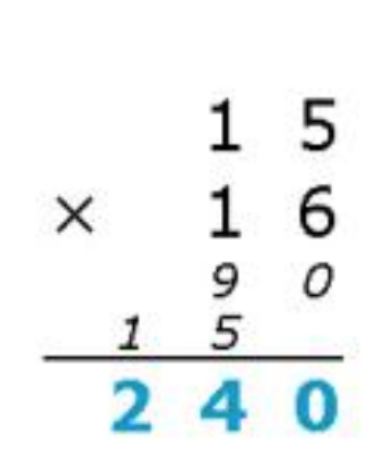由此可以看出，第一个数的第i项*第二个数的第j项应该放在i+j-1的位置。
搞定了前面，就可以进行乘法运算惹.，真的吹爆lh的算法：lh是先乘起来再处理，赶脚这样更好想也更好些一点；而且lh也没有用什么特判if之类的，让我这个蒟阵非常清楚自己在干什么qwq，比某ybt好多惹。
代码惹：
for(int i = 1;i <= lena;i++) for(int j = 1;j <= lenb;j++) c[i+j-1] = c[i+j-1]+a[i]*b[j]; //进行乘法运算 int len=lena+lenb-1;//暂时定义最后答案的长度为lena+lenb-1（或许会更长，一会再处理） for(int i=1;i<=len;i++){ c[i+1]+=c[i]/10;//又搞了个乌龙导致答案算错惹，这些大概都是我的弱点吧（写一遍错一遍qwq c[i]%=10; }
进行收尾的数据处理：
显然乘法计算时可能会有超出lena+lenb-1的情况，所以我们或许大概（啊呸）（那得麻溜的处理啊）需要处理一下：
这里有一个小细节，处理前方非零数位时，要用while而不是if,因为前面的数可能有若干个（突然想不没明白了qwq）
好惹，上代码：
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> using namespace std; char a1[100],b1[100]; int a[1000],b[1000],c[2000],lena,lenb,lenc; int main() { scanf("%s",a1); lena = strlen(a1); scanf("%s",b1); lenb = strlen(b1); for(int i = lena-1;i >= 0;i--)a[lena-i] = a1[i]-48;//把字符串存进数组中 for(int i = lenb-1;i >= 0;i--)b[lenb-i] = b1[i]-48; //刚刚搞了个大乌龙qwq（直接 a[lena-i] = a1[lena]-48;b[lenb-i] = b1[lenb]-48; for(int i = 1;i <= lena;i++) for(int j = 1;j <= lenb;j++){ c[i+j-1] += a[i]*b[j]; } //进行乘法运算 int len=lena+lenb-1;//暂时定义最后答案的长度为lena+lenb-1（或许会更长，一会再处理） for(int i=1;i<=len;i++){ c[i+1]+=c[i]/10; c[i]%=10; } while(c[len+1]!=0)len++; for(int i=len;i>=1;i--) printf("%d",c[i]); }//亲测15*3是对的qwq
2.高精度除法（这里只讲了高精/低精）：
其实高精除在乘法的基础上改一下核心语句就好惹，这里不细讲惹，我gun去写代码了，希望我核心的语句没有忘(写崩了写崩了！！！还是记不住qwq）:
找到了错误，感觉自己还是在小细节上不够仔细（buxianggenvsheng），像什么scanf没有加引执符，%d搞成%s（这个是输入字符数组b的时候忘记改过来了qwq）
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> using namespace std; char a1[100]; int a[1000],b,c[2000],lena; int main() { scanf("%s",a1); lena = strlen(a1); scanf("%d",&b); for(int i = lena-1;i >= 0;i--)a[lena-i] = a1[i]-48;//把字符串存进数组中 for(int i = lena;i >=1;i--){//除法是唯一一个从高位开始算的 c[i]=a[i]/b; a[i-1]+=(a[i]%b)*10;//意思是把这一位/b余下的余数加到下一位（比这一位低一位的）去（加到下一位就*10了呀）
} while(c[lena]==0)lena--; for(int i=lena;i>=1;i--) printf("%d",c[i]); }//亲测200/5有效
负数肿么办？？？
加法：一个数是负数：变为减法 两个数是负数：全部变为正数算加法，最后取负
减法：被减数是负数：全部变为正数算加法，最后取负 减数是负数：减数取负，变为加法 都是负数：都取负，变为减法，即（-减数）-（-被减数）
乘法：统计负数个数s 都变为非负数计算，若s为奇数，最后取负
- part2：模意义下的运算：
1.性质：
无除法运算，满足基本的交换律、分配率、结合律 对中间结果取模不影响最终答案
eg：快速幂
计算a^b % p = ?
法一：分治思想：
这个题洛谷有板子（不过编译失败是个什么鬼？？）（交了个板子题结果我炸了？？？）：
行吧经过我无数次（5次欸qwq）的没过板子emm我终于搞了个a了的代码：
分治的思想就是一分为二嘛，求a^b%p，可以先求a^（b/2）%p再相乘，然后再%p，要注意的是b不整除2的时候最后还要乘一个a，然后存答案的话要用long long，要不然会爆的（我就爆了***）
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> using namespace std; int a,b,p; int fz(int a,int b,int p){ long long ans=1; if(b==0)return 1;//当b=0时，a^0=1； ans=fz(a,b/2,p);//搞分治，b每次/2 ans=ans*ans%p; if(b%2==1) ans=ans*a%p;//乘回来b为奇数的那个a return ans; } int main(){ scanf("%d%d%d",&a,&b,&p); cout<<a<<"^"<<b<<" mod "<<p<<"=";//这个是洛谷板子题的要求qwq cout<<fz(a,b,p)%p<<endl;//一定要模p啊qwq }
法二：快速幂（板子又没过emm难到我数据又爆了？？好像还真是qwq ）：
行惹过了。突然想小反思一下：
感觉自己学信息奥赛这么久了，总是犯一些细节性的东西，基础还是不扎实，还需要努力盘一盘基础qwq
快速幂思想算是比较难理解代码的思想了，其实数学思想还好，比较好理解，就怕代码qwq
下面是某只zay的lh的解释？？
a^7 = a^1 * a^2 * a^4 2进制：111
a^11 = a^1 * a^2 * a^8 2进制：1011
a^25 = a^1 * a^8 * a^16 2进制：11001
所以首先计算出 a^1、 a^2、 a^4、 a^8 …，利用2进制表示出a，若第x位上为1，则乘a的x次方，若为0，则不乘。
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> using namespace std; long long a,b,p; int kuaisumi(long long a,long long b,long long p){//钟大佬kuaisumi（拼音）的操作天下无敌了 long long ans=1; while(b>0){ if(b&1)ans=ans*a%p;//满足第x位上是1，ans乘上a^（2^(x-1))； a=a*a%p;//这里一直计算着a^2k次方2k=2^(x-1); b/=2; } return ans; } int main(){ scanf("%d%d%d",&a,&b,&p); cout<<a<<"^"<<b<<" mod "<<p<<"="; cout<<kuaisumi(a,b,p)%p<<endl; }
费马小定理：
对于素数p和任意正整数a(0 ~ p-1)，有a^(p-1) ≡ 1(mod p)
b * a = t
t * a^(p-2) = b t/a=b
//在模p意义下除以一个数等于乘这个数的p-2次方
应用：计算C(n,m) % (10^9+7) 10^9+7是质数 n ,m<=10,0000 Query 10,0000
思路：C(n, m) = n! / ( (n-m)! * m! )
= n! * ( (n-m)! * m! )^(p-2)
= n! * ( (n-m)! )^(p-2) * (m! )^(p-2) 预处理任意n！、(n! )^(p-2)
这个预处理怕不是要炸掉？？？（顺便吐槽下lh的代码质量qwq真的是金牌吗？？
日常写标程写炸qwq
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<cmath> using namespace std; long long n,m; long long b[110000],d[110000]; long long p=1e9+7; long long pow(long long a,long long b,long long p){//快速幂求阶乘的p-2次方 long long ans=1; while(b>0){ if(b&1)ans=ans*a%p; a=a*a%p; b/=2; } return ans; } long long C(long long x,long long y){//求组合数的函数（思路见上 if(m>n)return -1; if(m==n||m==0)return 1; else return b[x]*d[x-y]%p*d[y]%p; } int main(){ scanf("%lld%lld",&n,&m); b[0]=1; for(int i=1;i<=100000;i++)b[i]=b[i-1]*i%p;//预处理1~100000的阶乘 for(int i=1;i<=100000;i++)d[i]=pow(b[i],p-2,p)%p;//预处理1~100000阶乘的p-2次方
cout<<C(n,m)<<endl; }
拓展：给定n,m,p求Cnm%p的值：
只需要改一下输入就可以了，变为输入三个数，p不再定义为1e9+7;
- part3：
1.最大公约数：
这里用到了辗转相除（mo）法：请自行百度：
代码qwq：
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<cmath> using namespace std; int a,b,x,y; int gcd(int a,int b){ if(b==0)return a; else return gcd(b,a%b); } int main(){ cin>>a>>b; cout<<gcd(a,b); }
最小公倍数：
这里有个小知识qwq：
lcm（a，b）*gcd（a，b）=a*b；
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<cmath> using namespace std; int a,b,x,y; int gcd(int a,int b){ if(b==0)return a; else return gcd(b,a%b); } int main(){ cin>>a>>b; cout<<a/gcd(a,b)*b; }
end-