Before:
线段覆盖问题#1:(我们所需要的)
一个区间,若干条线段,现在求最少多少条线段覆盖满整个区间
区间长度8,可选的覆盖线段[2,6],[1,4],[3,6],[3,7],[6,8],[2,4],[3,5]
1将每一个区间按照左端点递增顺序排列,拍完序后为[1,4],[2,4],[2,6],[3,5],[3,6],[3,7],[6,8]
2设置一个变量表示已经覆盖到的区域。再剩下的线段中找出所有左端点小于等于当前已经覆盖到的区域的右端点的线段中,右端点最大的线段在加入,直到已经覆盖全部的区域
3过程:
假设第一步加入[1,4],那么下一步能够选择的有[2,6],[3,5],[3,6],[3,7],由于7最大,所以下一步选择[3,7],最后一步只能选择[6,8],这个时候刚好达到了8退出,所选区间为3
4贪心证明:
需要最少的线段进行覆盖,那么选取的线段必然要尽量长,而已经覆盖到的区域之前的地方已经无所谓了,(可以理解成所有的可以覆盖的左端点都是已经覆盖到的地方),那么真正能够使得线段更成的是右端点,左端点没有太大的意义,所以选择右端点来覆盖
线段覆盖问题#2:(我们所补充的)
一个区间,若干条线段,现在求最少删去多少条线段覆盖满整个区间
分析:
先将线段排序,先按线段起点排序,若起点相同按终点排序,都是由小到大,依次遍历线段判断是否保留。
设当前线段为[ai,bi],之前保留的线段的最右边的点为now,考虑以下情况:
1、ai>=now,即当前线段和之前保留的线段不重叠,那么直接保留当前线段(ans++),更新now=bi.
2、ai<now,当前线段和之前保留的线段有重叠,再分情况考虑:
(1)若bi<=now,证明当前线段完全被之前保留线段的区域包含(因为已经排序,所以当前线段的起点一定大于等于之前的线段,bi<now证明终点小于等于之前线段,所以被包含),那么证明当前线段更优(一条线段被另一条完全包含,显然取短的线段更优,即贪心),更新now=bi,但是结果计数(ans)不变.
(2)若bi>now,证明当前线段一部分和之前重叠,一部分不重叠,那么为了对后续线段影响最小,即now尽量小,用贪心法则,当前线段被舍弃,结果计数(ans)不变.
题目思路:
- 先bfs每一个沿湖城市所对应的沿沙漠城市。
- 沙漠城市如果有没有被bfs到的,说明有无法被覆盖到的点,直接进入无解状态;若全部都被bfs到了,进行线段覆盖,在沙漠里寻找最少的区间。
证明对于一个蓄水池,不可能出现流到沙漠地带时有间隔的情况,即:
不能出现从一个点i可以流到j-1和j+1却不能流到j的情况;
Why?
如果由i可以流到j-1和j+1却不能流到j,则j不可能被流到:
假设i流到j-1,j+1却没有流到j,那么h(j+1),h(j-1)<h(j),因此水无法从上下两边流到j,那么水只能从左边流到j。
假设有一点k可以到j
那么k到j的路线与i到j+1或j-1的路线一定有相交的地方,则通过i一定可以流到j,矛盾
即对于每一个沿湖城市,可以到达的沙漠城市都是一个区间。(线段覆盖问题)
讲一下毒瘤数据???
毒瘤数据#1:
n=1,只有一横行
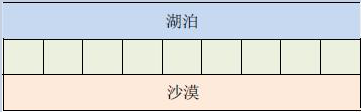

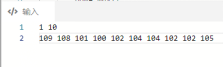

看一下输入输出,这样的话会有几个点没有被加进已经被覆盖的数组中,定睛一看输入,我们发现爆0的地方都是区间最高点,当流到它时,接下来的地方就需要再建一个水库,因此未赋为1的点其实就是我们建水库的点。
加个特判:
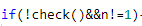
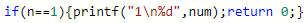
毒瘤数据#2:
一个大到你无法想象的数据:
显然会t啊qwq?这时候显然需要优化啊。
一个简单的优化:在搜索第一行的每个点时,判断一下这个点的左边和这个点的右边,如果它比两边都高,说明没有点可以流到它,就bfs它,否则假设它左边或右边比它高,它一定可以看作是从左侧或右侧流过来的。
#include<bits/stdc++.h> using namespace std; int n,m,num,now,ans,_max; int a[501][501]; bool vis[501][501],pan[501];//vis每次bfs清空,表示某个点是否被搜索到过 //pan记录最后一行的点是否被覆盖到了 int dx[4]={0,0,1,-1}; int dy[4]={1,-1,0,0}; struct coder{ int l,r; coder(){l=2147483647;r=0;}//神奇的赋值构造函数?感谢sy?是在下才疏学浅了 }b[501]; struct hyh{//用于bfs,记录横纵坐标 int x,y; }; bool cmp(coder a,coder b){//按左端点从小到大排序 return a.l<b.l; } hyh _hyh(int x,int y){hyh rtn;rtn.x=x;rtn.y=y;return rtn;}//赋值函数,与构造函数用途相同,但我不会写构造 bool check(){//判断最后一行是否都能被覆盖 int rtn=1; for(int i=1;i<=m;i++) if(!pan[i]){rtn=0;num++;} return rtn; } bool zpd(int xx,int yy){//用于bfs时判断是否可以走 return vis[xx][yy]==0&&xx>=1&&yy>=1&&xx<=n&&yy<=m; } queue<hyh> q; void bfs(int x,const int f){ memset(vis,0,sizeof(vis)); q.push(_hyh(1,f)); vis[1][f]=1; while(!q.empty()){ hyh c=q.front(); q.pop(); for(int i=0;i<4;i++){ int xx=c.x,yy=c.y; xx+=dx[i];yy+=dy[i]; if(a[xx][yy]<a[c.x][c.y]&&zpd(xx,yy)){//满足从高流到低并且可以走 if(xx==n){//如果搜到的点是最后一行的 //记录第一行某个点能流到的最后一行的区间的左右端点分别是什么 : if(b[f].l>yy) b[f].l=yy; if(b[f].r<yy) b[f].r=yy; pan[yy]=1;//标记最后一行的某个点为可以走到 } q.push(_hyh(xx,yy)); vis[xx][yy]=1; } } } } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) scanf("%d",&a[i][j]); for(int i=1;i<=m;i++)//优化:如果某个点左右两边的点都比这个点要低,bfs if(a[1][i]>=a[1][i-1]&&a[1][i]>=a[1][i+1]) bfs(a[1][i],i); if(!check()&&n!=1){ //判断是否可以全部覆盖,如果不可以,直接进入无解状态(注意特殊的数据n==1) printf("0 "); printf("%d",num); return 0; } if(n==1){printf("1 %d",num);return 0;}//n==1的特判 sort(b+1,b+m+1,cmp);//进行线段覆盖,把线段按区间左端点位置排序; now=1;_max=0;//now我就认为是右端点了qwq,_max记录右端点的最大值; while(now<=m){//当全部被覆盖,停止 for(int i=1;i<=m;i++) if(b[i].l<=now)//如果这个点左端点在当前覆盖区间之内 _max=max(_max,b[i].r); //找最大的右端点 ans++;//记录加了一个水库 now=_max+1;//现在最大右端点更新为_max+1;(因为下一个线段的左端点可以刚好与之前的覆盖区间刚好相连): //------ now=6,加入一个left=7,right=9的点 --------- (刚好相连) } printf("1 "); printf("%d",ans); return 0; }
最后插一句:why小姐姐说过了,无论何时,都要保持一个优雅的码风~~~(然而我的码风好像并不优雅