停更20天祭qwq(因为去准备推荐生考试了一直在自习qwq)

这道题的前置知识是DP,可以参考=>【五一qbxt】day3 动态规划 鬼知道我写的是什么emm
这道题真的做了超级久了,大约从五六号的开始做吧,推荐生考试一直耽搁了qwq
鹅且——我wa了好多好多次qwq,也真是令人质壁分离了。
一个O(n)的动态规划的思路:
准备好多好多不同的数组:
- pre[i] 表示位置 i 之前 (包括位置 i) 最大的满足最低消费的咖啡店位置
- pos[j] 表示第 j 种颜色客栈目前出现的最大的位置
- tot[j] 表示第 j 种颜色客栈目前出现的总个数
- res[i] 表示位置 i 作为右端点能组成多少组配对
可能有点抽象,so:

现在已经知道一组并不毒瘤的良心数据:
5 2 3
0 5
1 3
0 2
1 4
1 5(其实就是洛谷的样例)
辣么:
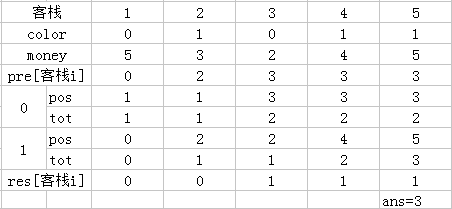
这样大概可能应该会好理解一点吧qwq。
前面的pos与tot都是记录的当前值,因此很显然我们要一边处理一边DP:
首先输入一组color与money
判断新输入的这个客栈是否满足最低消费的需要,如果满足,pre[i]=i;否则显然pre[i]的值与上一个客栈的pre相同emm

注意:处理完pre后要接着去处理res,处理的顺序应为:pre=>res=>tot&pos;
处理res:(转移方程)
把选择每种颜色的客栈都枚举一下:

判断当前客栈与前一个颜色相同的客栈之间是否有满足最低消费的另一客栈,如果没有,前一个颜色相同的客栈的组合数就等于当前客栈的组合数。
举个例子:
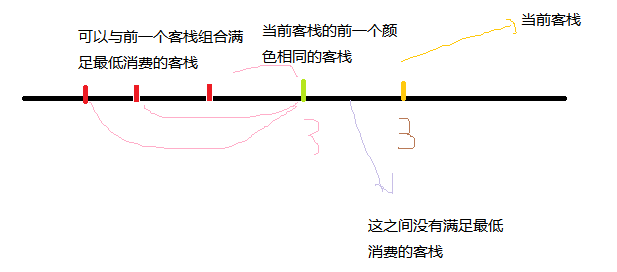
如果有,那么对于i之前的每一个与之颜色相同的客栈都可以与i配对组成一种方案,即pre[i]=tot[c]
这样转移方程就有了:
然后对于每个方案都+起来,就是最后的ans;
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> const int maxn = 200010; const int maxk = 100; using namespace std; int n,k,p,c,m,ans,maxl; int pre[maxn],pos[maxn],tot[maxn],res[maxn]; int main(){ scanf("%d%d%d",&n,&k,&p); for(int i = 1;i <= n;i++){ scanf("%d%d",&c,&m); if(m <= p) pre[i] = i; else pre[i] = pre[i-1]; for(int j = 0;j < k;j++){ if(pre[i] < pos[c]) res[i] = res[pos[c]]; else res[i] = tot[c]; } pos[c] = i; tot[c]++; ans += res[i]; } cout<<ans<<endl; }
end-