分治:
分治分治,分而治之;分治算法就是将一个大问题划分为几个更小规模的问题并加以解决,通过解决子问题最后解决总问题。
分治算法在OI中的运用主要在两个方面:
1.基于二分查找、三分查找的运用
2.将题目划分为更细小的子问题的运用
我们将按顺序来讲解这两个方面
二分-
二分的本质是:在一个有序区间内确定一个边界,在边界的一边的元素满足某种性质,而另外一边不满足;
故二分经常用于解决如下类型的问题:
1.简单的二分查找
2.二分答案(即求一个单调函数在满足某个性质下的最值)
3.最值的最值(最常见的二分题类型)
从high level理解二分:
二分求得实际是一个边界;
二分需要有序,有序可以是大小,也可以是其他奇奇怪怪的问题;
最值的最值:最大的最小,最小的最大=>想二分=>优秀写法;
二分模板:

讲真的我不是很喜欢这样写二分
Noip2012借教室

利用差分的思想打标记,然后一遍前缀和求出每天借教室的数量;O(n+m);

然后二分,O(n)比较是否合法qwq

加线懵逼

突然安利的网站:




U 1~num范围内,被x整除的数个数;
V 1~num范围内,被y整除的数个数;
W 1~num范围内,被x*y整除的数个数;
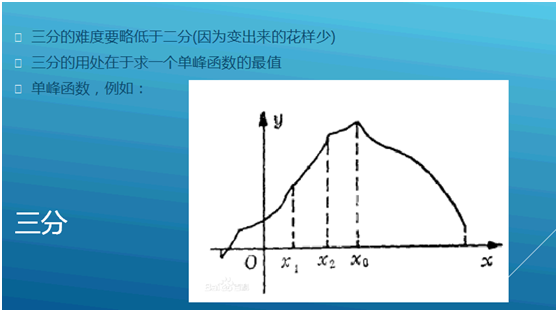
复杂度O(log3/2N)
Eps:
首先讲:1e-8就是10的-8次方;
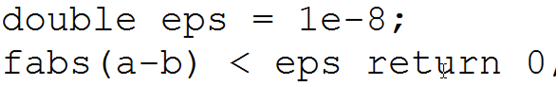

非单峰函数:
将每个峰割出来,然后每一段求一个最优;
怎么割峰呢,只要你割的够细,每一部分都是峰
Len:每段长度

分块-


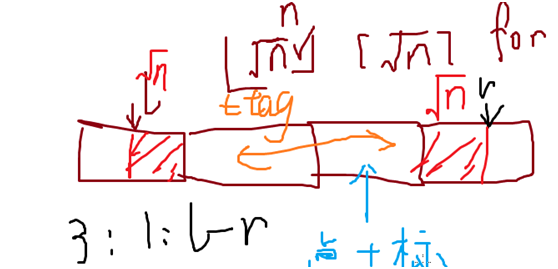
先把长为n的数组分√n块,每个长度是√n左右;
1.朴素想法,暴力。
找l在哪一块,r在哪一块
情况1:l,r在同一块 复杂度不超过o(√n)
2:l,r在相邻块里 复杂度不超过o(2√n);
3:l,r距离一段距离;l,r所在的块计算出来,其余中间块打标记;最多打o(√n)个块;
2.排序神仙orz
首先分块,分块时要将这个块里数据排序,;
查询:

- 在同一个块块里 O(√n)暴力for
- 相邻块O(2√n)
- 不相邻;
首先在a数组中查询左端点l所在块中,l右侧有多少满足的
同理右端点r也跑一下;
然后对于中间的块,每一个块都在b数组中跑一个二分就好了呢qwq

暴力加加在a上,然后再排序;其他的与1的加相同;
修改:先将l所在块和r所在块进行暴力并且在b数组中重新排序,其他中间的块打标记,当查询这个块时,不再查询x,而是查询 x-此块打的标记;
3.精髓:一个long long的整数最多开方6次,0开方为0,1开方为1;
先分块,对区间分√n块,每次开方时,for l~r,全部开方,当某个块只有0或1时,打个标记,就不用再开方了;
复杂度:O(6n);

记录离当前颜色最近的相同颜色的球的位置;

最后一句查询可以用2来做
修改:对每个颜色维护一个set;
把每个颜色丢进去;????
要满足于代码短,代码优秀;
搜索:

最短路=>广搜
求所有解=>深搜 干净代码+清晰思路

广搜的节点要开多一点;不要如此吝啬;

一般用于求最优解
轮次搜:
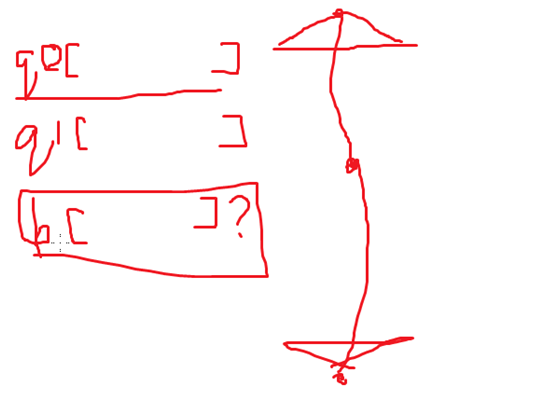
q0和q1交替搜索,然后直到交头;会减少垃圾节点;
迭代加深搜索:


搜到d层就不搜了,如果没有解,深度d++;
适合很深很宽的搜索树;
枚举完深度,选用深搜

开始连接:https://www.cnblogs.com/zhuier-xquan/p/10991869.html

当你觉得题面很复杂,数据范围又很小,考虑搜索;
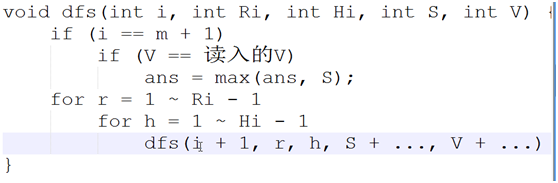
莫得剪枝↑
剪枝1:现在体积超过n,无需再跑,直接return;
剪枝2:当前算的表面积比我们目前求得最优解大,return;

强夸剪枝二!